קומבינטוריקה, תורת הגרפים
תורת הגרפים חוקרת גרפים, שהם מבנים המורכבים מקדקודים (צמתים) וקשתות המחברות ביניהם. היא משמשת למדידת יחסים. שאלות מכסות נושאים כמו מסלולים, מעגלים, קשירות, צביעת גרפים, עצים וניתוח תכונות של סוגי גרפים שונים.
-
הזבוב על האוקטהדרון
"תראה," אמר הפרופסור לעמיתו, "אני צופה בזבוב הזה על האוקטהדרון, והוא מגביל את הליכותיו אך ורק לקצוות. מה יכולה להיות הסיבה שלו להימנע מהצדדים?"
"אולי הוא מנסה לפתור איזושהי בעיית מסלול," הציע השני. "בהנחה שהוא מתחיל מנקודת העליונה, כמה מסלולים שונים יש שבהם הוא יכול ללכת על כל הקצוות, מבלי ללכת פעמיים לאורך אותו קצה בכל מסלול?"
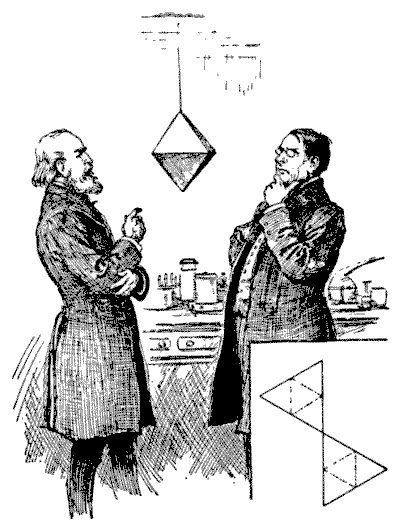
הבעיה הייתה קשה יותר ממה שהם ציפו, ולאחר שעבדו עליה ברגעי הפנאי במשך מספר ימים התוצאות שלהם לא הסכימו — למעשה, שניהם טעו. אם הקורא מופתע מכישלונם, שינסה בעצמו את החידה הקטנה. אסביר רק שהאוקטהדרון הוא אחד מחמשת הגופים הרגילים, או האפלטוניים, והוא תחום תחת שמונה משולשים שווים ושווי צלעות. אם תגזור את שני חלקי הקרטון בצורה המוצגת בשולי האיור, תגזור חצי דרך לאורך הקווים המקווקווים ואז תכופף אותם ותחבר אותם, תקבל אוקטהדרון מושלם. בכל מסלול על פני כל הקצוות יתגלה שהזבוב חייב להסתיים בנקודת המוצא בראש.
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 245
-
הפאזל של האיקוסהדרון
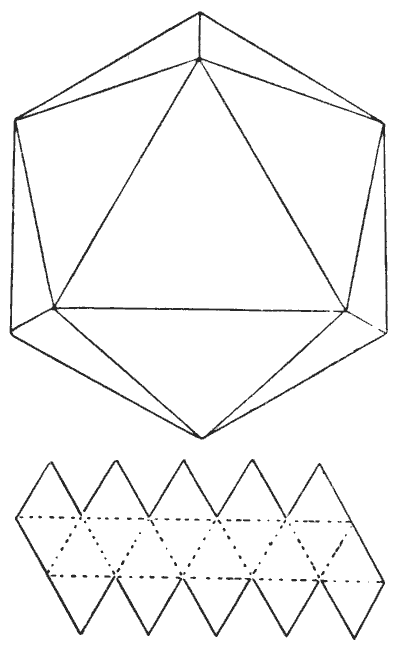
האיקוסהדרון הוא עוד אחד מחמשת הגופים הרגילים, או האפלטוניים, שכל צדדיהם, זוויותיהם ומישוריהם דומים ושווים. הוא תחום על ידי עשרים משולשים שווי צלעות דומים. אם תגזרו חתיכת קרטון בצורה המוצגת בדיאגרמה הקטנה יותר, ותחתכו חצי עובי לאורך הקווים המקווקווים, היא תתקפל ותיצור איקוסהדרון מושלם.
ובכן, גוף אפלטוני לא בהכרח מציין גוף שמימי; אבל זה יתאים למטרת הפאזל שלנו אם נניח שיש כוכב לכת ראוי למגורים בצורה הזו. נניח גם שבשל שפע מים, היבשה היחידה נמצאת לאורך הקצוות, ושלתושבים אין ידע בניווט. אם כל אחד מהקצוות האלה באורך `10,000` מיילים, ומטייל בודד ממוקם בקוטב הצפוני (הנקודה הגבוהה ביותר המוצגת), כמה רחוק הוא יצטרך לנסוע לפני שהוא יבקר בכל חלק ראוי למגורים בכוכב הלכת — כלומר, יחצה כל אחד מהקצוות?
 מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 246
-
בדיקת מכרה
הדיאגרמה אמורה לייצג את המעברים או הגלריות במכרה. נניח שכל מעבר, מ-A ל-B, מ-B ל-C, מ-C ל-H, מ-H ל-I, וכן הלאה, הוא באורך פרלונג אחד. ניתן לראות שיש שלושים ואחד מהמעברים האלה. כעת, פקיד צריך לבדוק את כולם, והוא יורד דרך הפיר לנקודה A. כמה רחוק הוא צריך לנסוע, ואיזה מסלול אתה ממליץ? הקורא עשוי לומר תחילה, "מכיוון שיש שלושים ואחד מעברים, כל אחד באורך פרלונג, הוא יצטרך לנסוע שלושים ואחד פרלונגים בדיוק." אבל זה מניח שהוא לעולם לא יצטרך לעבור לאורך מעבר יותר מפעם אחת, וזה לא המקרה. קח את העיפרון שלך ונסה למצוא את המסלול הקצר ביותר. עד מהרה תגלה שיש מקום לשיקול דעת ניכר. למעשה, זו חידה מבלבלת.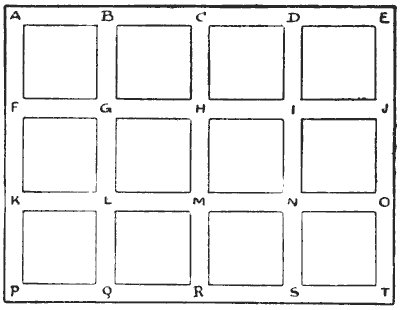 מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 247
-
החידה של המלח
המלח המתואר באיור הצהיר שמאז נעוריו עסק במסחר עם כלי שיט קטן בין כעשרים איים קטנים באוקיינוס השקט. הוא סיפק את התרשים המחוספס שנתתי ממנו העתק, והסביר שהקווים מאי לאי מייצגים את המסלולים היחידים שהוא אי פעם אימץ. הוא תמיד התחיל מאי A בתחילת העונה, ואז ביקר בכל אי פעם אחת, ופעם אחת בלבד, וסיים את סיורו בנקודת ההתחלה A. אבל הוא תמיד דחה את ביקורו ב-C ככל האפשר, מטעמי מסחר שאיני צריך להיכנס אליהם. החידה היא לגלות את המסלול המדויק שלו, וניתן לעשות זאת בוודאות. קחו את העיפרון שלכם, ומתחילים ב-A, נסו לאתר אותו. אם תרשמו את האיים בסדר שבו אתם מבקרים בהם - לדוגמה, A, I, O, L, G וכו' - תוכלו לראות מיד אם ביקרתם באי פעמיים או השמטתם איזה מהם. כמובן, יש להתעלם מחציית הקווים - כלומר, עליכם להמשיך במסלולכם ישירות, ואין לכם רשות לעבור בצומת ולהמשיך בכיוון אחר. אין שום טריק מסוג זה בחידה. המלח ידע את המסלול הטוב ביותר. האם אתה יכול למצוא אותו? מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 249
-
הטיול הגדול
אחת החידות היומיומיות של החיים היא תכנון מסלולים. אם אתם יוצאים לחופשה על אופניים, או לטיול מוטורי, תמיד עולה השאלה כיצד לנצל את הזמן והמשאבים שלכם בצורה הטובה ביותר. החלטתם להגיע למקום מסוים, לכלול ביקורים בעיר כזו וכזו, לנסות לראות משהו מעניין במיוחד במקום אחר, ואולי לנסות לבקר חבר ותיק בנקודה שלא תוציא אתכם בהרבה מהדרך. אז אתם צריכים לתכנן את המסלול שלכם כדי להימנע מכבישים גרועים, אזורים לא מעניינים, ואם אפשר, מהצורך לחזור באותה דרך שבה נסעתם. עם מפה לפניכם, ניגשים לפתרון החידה המעניינת. אציג לכם שאלה קטנה המבוססת על קווים אלה.
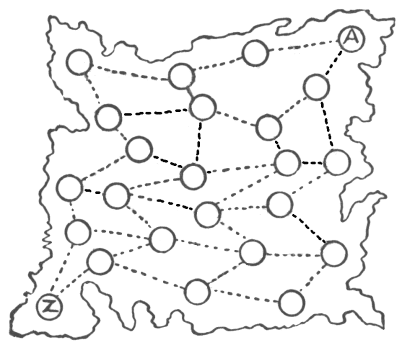
אני מציג מפה גסה של מדינה—אין צורך לומר איזו מדינה—העיגולים מייצגים ערים והקווים המקווקווים את מסילות הברזל המחברות ביניהן. עכשיו, בעיר המסומנת A חי אדם שנולד שם, ובמשך כל חייו מעולם לא עזב את מקום הולדתו. מנעוריו הוא היה חרוץ מאוד, דבק בעקביות במקצועו, ולא היה לו רצון לשוטט בחוץ. עם זאת, בהגיעו לגיל חמישים הוא החליט לראות קצת מהמדינה שלו, ובמיוחד לבקר חבר ותיק מאוד שגר בעיר המסומנת Z. מה שהוא הציע היה כזה: שהוא יתחיל מביתו, ייכנס לכל עיר פעם אחת בלבד, ויסיים את מסעו ב-Z. מכיוון שהוא החליט לבצע את הטיול הגדול הזה ברכבת בלבד, הוא התקשה קצת לתכנן את המסלול שלו, אבל בסופו של דבר הוא הצליח לעשות זאת. איך הוא הצליח? אל תשכחו שצריך לבקר בכל עיר פעם אחת, ולא יותר מפעם אחת.
 מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 250
-
מים, גז וחשמל
ישנם כחצי תריסר חידות, עתיקות כימי ההיסטוריה, שצצות ועולות תדיר, וכמעט שאין חודש בשנה שלא מביא עמו פניות בנוגע לפתרונן. מדי פעם אחת מהן, שאדם חשב שהיא הר געש כבוי, מתפרצת בצורה מפתיעה. קיבלתי מספר יוצא דופן של מכתבים בנוגע לחידה העתיקה שכיניתי "מים, גז וחשמל". היא עתיקה בהרבה מתאורת חשמל, או אפילו גז, אבל הלבוש החדש מעדכן אותה. החידה היא להניח מים, גז וחשמל, מ-W, G ו-E, לכל אחד משלושת הבתים, A, B ו-C, מבלי שאף צינור יחצה צינור אחר. קחו את העיפרון וציירו קווים המראים כיצד יש לעשות זאת. עד מהרה תמצאו את עצמכם נתקלים בקשיים.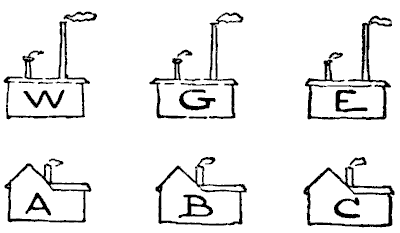 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 251
-
חידה לנהגים
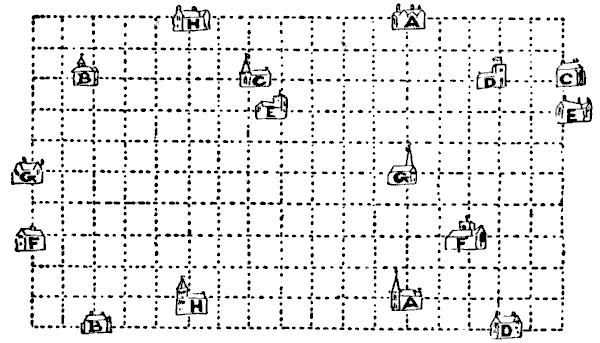 שמונה נהגים נסעו לכנסייה בוקר אחד. בתים וכנסיות מתאימים, יחד עם הכבישים היחידים הזמינים (הקווים המקווקווים), מוצגים. אחד נסע מביתו א' לכנסייה א' שלו, אחר מביתו ב' לכנסייה ב' שלו, אחר מ-ג' ל-ג', וכן הלאה, אבל לאחר מכן התגלה שאף נהג לא חצה את מסלול המכונית האחרת. קחו את העיפרון שלכם ונסו לאתר את המסלולים השונים שלהם.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
שמונה נהגים נסעו לכנסייה בוקר אחד. בתים וכנסיות מתאימים, יחד עם הכבישים היחידים הזמינים (הקווים המקווקווים), מוצגים. אחד נסע מביתו א' לכנסייה א' שלו, אחר מביתו ב' לכנסייה ב' שלו, אחר מ-ג' ל-ג', וכן הלאה, אבל לאחר מכן התגלה שאף נהג לא חצה את מסלול המכונית האחרת. קחו את העיפרון שלכם ונסו לאתר את המסלולים השונים שלהם.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 252
-
טיול המכונית
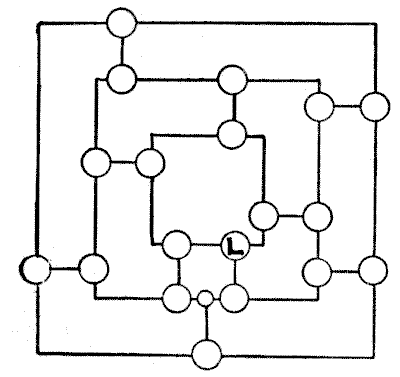 בתרשים לעיל, העיגולים מייצגים ערים והקווים מייצגים כבישים טובים. בכמה דרכים שונות בדיוק יכול נהג, היוצא מלונדון (מסומנת באות L), לערוך סיור בכל הערים הללו, לבקר בכל עיר פעם אחת בלבד בסיור, ולחזור תמיד ללונדון בנסיעה האחרונה? ההיפוך המדויק של כל מסלול אינו נחשב לשונה.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
בתרשים לעיל, העיגולים מייצגים ערים והקווים מייצגים כבישים טובים. בכמה דרכים שונות בדיוק יכול נהג, היוצא מלונדון (מסומנת באות L), לערוך סיור בכל הערים הללו, לבקר בכל עיר פעם אחת בלבד בסיור, ולחזור תמיד ללונדון בנסיעה האחרונה? ההיפוך המדויק של כל מסלול אינו נחשב לשונה.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 254
-
הנזיר והגשרים
במקרה הזה אני מציג תוכנית גסה של נהר עם אי וחמישה גשרים. בצד אחד של הנהר נמצא מנזר, ובצד השני נראה נזיר בחזית. כעת, הנזיר החליט שהוא יעבור כל גשר פעם אחת, ורק פעם אחת, בדרכו חזרה למנזר. זה כמובן די קל לעשות, אבל בדרך הוא חשב לעצמו, "אני תוהה כמה מסלולים שונים יש מהם יכולתי לבחור." האם הייתם יכולים לומר לו? זו החידה. קחו את העיפרון שלכם ועקבו אחר מסלול שייקח אתכם פעם אחת על פני כל חמשת הגשרים. לאחר מכן עקבו אחר מסלול שני, אחר כך שלישי, ובדקו אם אתם יכולים לספור את כל הווריאציות. תגלו שהקושי הוא כפול: עליכם להימנע מלהפיל מסלולים מצד אחד ולספור את אותם מסלולים יותר מפעם אחת מצד שני.
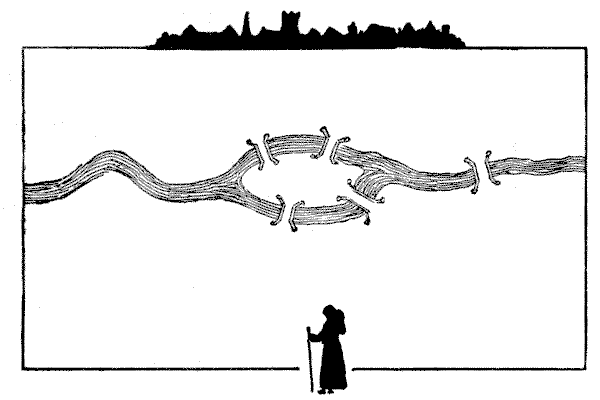 מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 261
-
מסע הצריח
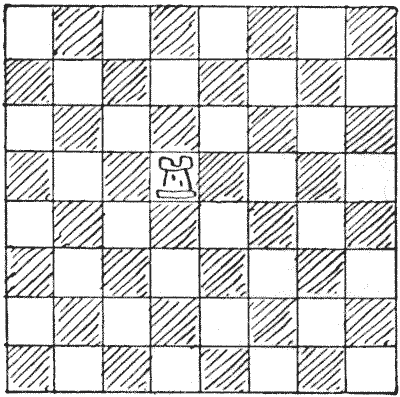 החידה היא להזיז את הצריח הבודד על פני כל הלוח, כך שהוא יבקר בכל משבצת בלוח פעם אחת בלבד, ויסיים את מסעו במשבצת ממנה הוא התחיל. עליכם לעשות זאת במספר המהלכים המינימלי האפשרי, ואם לא תהיו זהירים מאוד, תבצעו מהלך אחד יותר מדי. כמובן, משבצת נחשבת כ"מבוקרת" בין אם רק עוברים מעליה או הופכים אותה לתחנת עצירה, ולא נתווכח על הנקודה האם המשבצת המקורית מבוקרת פעמיים בפועל. נניח שהיא לא.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
החידה היא להזיז את הצריח הבודד על פני כל הלוח, כך שהוא יבקר בכל משבצת בלוח פעם אחת בלבד, ויסיים את מסעו במשבצת ממנה הוא התחיל. עליכם לעשות זאת במספר המהלכים המינימלי האפשרי, ואם לא תהיו זהירים מאוד, תבצעו מהלך אחד יותר מדי. כמובן, משבצת נחשבת כ"מבוקרת" בין אם רק עוברים מעליה או הופכים אותה לתחנת עצירה, ולא נתווכח על הנקודה האם המשבצת המקורית מבוקרת פעמיים בפועל. נניח שהיא לא.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 320