Amusements in Mathematics, Henry Ernest Dudeney
-
Question 181 - THE THREE RAILWAY STATIONS
As I sat in a railway carriage I noticed at the other end of the compartment a worthy squire, whom I knew by sight, engaged in conversation with another passenger, who was evidently a friend of his.
"How far have you to drive to your place from the railway station?" asked the stranger.
"Well," replied the squire, "if I get out at Appleford, it is just the same distance as if I go to Bridgefield, another fifteen miles farther on; and if I changed at Appleford and went thirteen miles from there to Carterton, it would still be the same distance. You see, I am equidistant from the three stations, so I get a good choice of trains."
Now I happened to know that Bridgefield is just fourteen miles from Carterton, so I amused myself in working out the exact distance that the squire had to drive home whichever station he got out at. What was the distance?
Topics:Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Algebra -> Word Problems -
Question 182 - THE GARDEN PUZZLE
Professor Rackbrain tells me that he was recently smoking a friendly pipe under a tree in the garden of a country acquaintance. The garden was enclosed by four straight walls, and his friend informed him that he had measured these and found the lengths to be `80, 45, 100`, and `63` yards respectively. "Then," said the professor, "we can calculate the exact area of the garden." "Impossible," his host replied, "because you can get an infinite number of different shapes with those four sides." "But you forget," Rackbrane said, with a twinkle in his eye, "that you told me once you had planted this tree equidistant from all the four corners of the garden." Can you work out the garden's area?Topics:Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Algebra -> Equations Algebra -> Word Problems -
Question 183 - DRAWING A SPIRAL
If you hold the page horizontally and give it a quick rotary motion while looking at the centre of the spiral, it will appear to revolve. Perhaps a good many readers are acquainted with this little optical illusion. But the puzzle is to show how I was able to draw this spiral with so much exactitude without using anything but a pair of compasses and the sheet of paper on which the diagram was made. How would you proceed in such circumstances?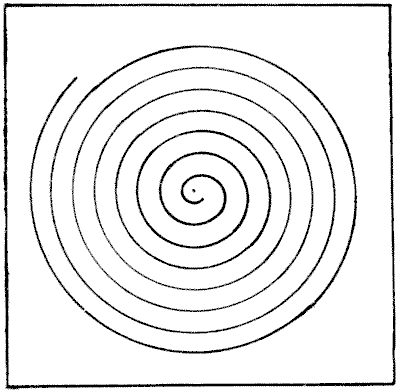 Topics:Geometry -> Plane Geometry -> Circles
Topics:Geometry -> Plane Geometry -> Circles -
Question 184 - HOW TO DRAW AN OVAL
Can you draw a perfect oval on a sheet of paper with one sweep of the compasses? It is one of the easiest things in the world when you know how.Topics:Geometry -
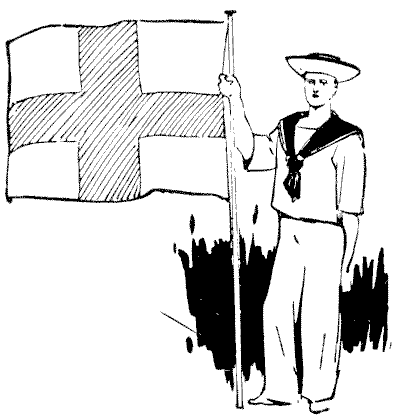
Question 185 - ST. GEORGE'S BANNER
At a celebration of the national festival of St. George's Day I was contemplating the familiar banner of the patron saint of our country. We all know the red cross on a white ground, shown in our illustration. This is the banner of St. George. The banner of St. Andrew (Scotland) is a white "St. Andrew's Cross" on a blue ground. That of St. Patrick (Ireland) is a similar cross in red on a white ground. These three are united in one to form our Union Jack.
Now on looking at St. George's banner it occurred to me that the following question would make a simple but pretty little puzzle. Supposing the flag measures four feet by three feet, how wide must the arm of the cross be if it is required that there shall be used just the same quantity of red and of white bunting?
-
Question 186 - THE CLOTHES LINE PUZZLE
A boy tied a clothes line from the top of each of two poles to the base of the other. He then proposed to his father the following question. As one pole was exactly seven feet above the ground and the other exactly five feet, what was the height from the ground where the two cords crossed one another? -
Question 187 - THE MILKMAID PUZZLE
Here is a little pastoral puzzle that the reader may, at first sight, be led into supposing is very profound, involving deep calculations. He may even say that it is quite impossible to give any answer unless we are told something definite as to the distances. And yet it is really quite "childlike and bland."

In the corner of a field is seen a milkmaid milking a cow, and on the other side of the field is the dairy where the extract has to be deposited. But it has been noticed that the young woman always goes down to the river with her pail before returning to the dairy. Here the suspicious reader will perhaps ask why she pays these visits to the river. I can only reply that it is no business of ours. The alleged milk is entirely for local consumption.
"Where are you going to, my pretty maid?"
"Down to the river, sir," she said.
"I'll not choose your dairy, my pretty maid."
"Nobody axed you, sir," she said.
If one had any curiosity in the matter, such an independent spirit would entirely disarm one. So we will pass from the point of commercial morality to the subject of the puzzle.Draw a line from the milking-stool down to the river and thence to the door of the dairy, which shall indicate the shortest possible route for the milkmaid. That is all. It is quite easy to indicate the exact spot on the bank of the river to which she should direct her steps if she wants as short a walk as possible. Can you find that spot?
-
Question 188 - THE BALL PROBLEM

A stonemason was engaged the other day in cutting out a round ball for the purpose of some architectural decoration, when a smart schoolboy came upon the scene.
"Look here," said the mason, "you seem to be a sharp youngster, can you tell me this? If I placed this ball on the level ground, how many other balls of the same size could I lay around it (also on the ground) so that every ball should touch this one?"
The boy at once gave the correct answer, and then put this little question to the mason:—
"If the surface of that ball contained just as many square feet as its volume contained cubic feet, what would be the length of its diameter?"
The stonemason could not give an answer. Could you have replied correctly to the mason's and the boy's questions?
-
Question 189 - THE YORKSHIRE ESTATES
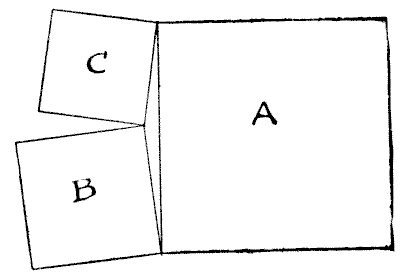
I was on a visit to one of the large towns of Yorkshire. While walking to the railway station on the day of my departure a man thrust a hand-bill upon me, and I took this into the railway carriage and read it at my leisure. It informed me that three Yorkshire neighbouring estates were to be offered for sale. Each estate was square in shape, and they joined one another at their corners, just as shown in the diagram. Estate A contains exactly `370` acres, B contains `116` acres, and C `74` acres.
Now, the little triangular bit of land enclosed by the three square estates was not offered for sale, and, for no reason in particular, I became curious as to the area of that piece. How many acres did it contain?
Topics:Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Pythagorean Theorem -
Question 190 - FARMER WURZEL'S ESTATE
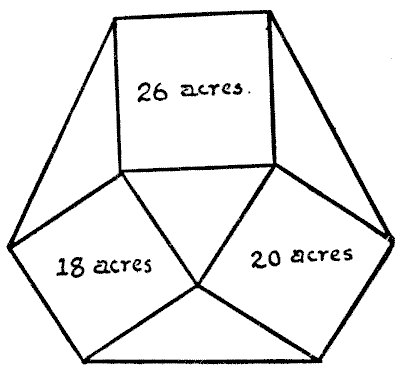
I will now present another land problem. The demonstration of the answer that I shall give will, I think, be found both interesting and easy of comprehension.
Farmer Wurzel owned the three square fields shown in the annexed plan, containing respectively `18, 20`, and `26` acres. In order to get a ring-fence round his property he bought the four intervening triangular fields. The puzzle is to discover what was then the whole area of his estate.
Topics:Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Pythagorean Theorem