Combinatorics

Combinatorics is the art of counting. It deals with selections, arrangements, and combinations of objects. Questions involve determining the number of ways to perform tasks, arrange items (permutations), or choose subsets (combinations), often using principles like the product rule and sum rule.

Pigeonhole Principle Double Counting Binomial Coefficients and Pascal's Triangle Product Rule / Rule of Product Graph Theory Matchings Induction (Mathematical Induction) Game Theory Combinatorial Geometry Invariants Case Analysis / Checking Cases Processes / Procedures Number Tables Colorings

• Question

  Cut the given shape into eight congruent parts:

  

  Topics:

  Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

• Question

  Divide the given shape into 16 congruent parts:

  

  Topics:

  Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

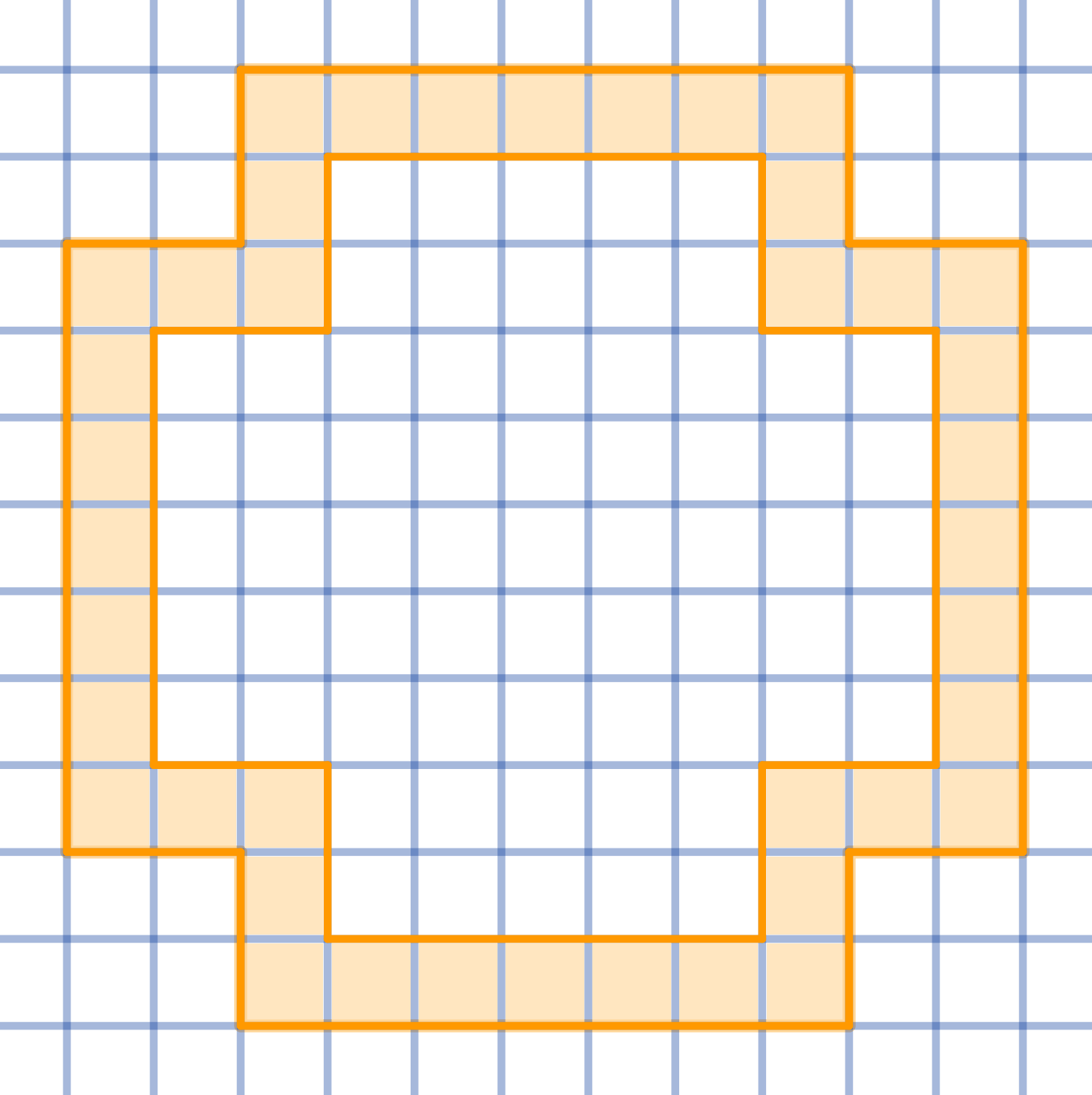
• Ants on a Stick

  On a stick that is one meter long, there are `10` ants, `5` from each side, at distances of one centimeter (see the picture). The ants on the left side of the stick move to the right, and the ants on the right side of the stick move to the left. The speed of each ant is constant and equal to one centimeter per second. When two ants meet, they both reverse direction and start moving away from each other. When any ant reaches the end of the stick, it falls off (ants are particularly stupid creatures).

  

  a. Will all the ants fall off the stick, and if so, in how much time?

  b. How many collisions will occur between the ants?

  Topics:

  Combinatorics -> Invariants Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures

• Milk and Coffee

  A. Hannah has two cups, one with milk and the other with coffee. The amounts of milk and coffee are the same. Hannah transfers two teaspoons of milk into the cup with coffee, mixes, and then transfers two teaspoons from the cup of coffee into the milk. Currently, she has two cups each containing a mixture of coffee and milk. What is greater – the amount of milk in the cup of coffee or the amount of coffee in the cup of milk?

  B. The same question, but this time Hannah adds milk to the coffee without mixing.

  Topics:

  Combinatorics -> Invariants Logic -> Reasoning / Logic

• The Clubs

  In the grade, there are `70` children. Of these, `27` go to theater club, `32` sing in the choir, and `22` do Judo. In the theater club, there are `10` children from the choir, in the choir there are `6` children from Judo, and in Judo there are `8` children who also study theater. Three children also go to theater club, Judo, and sing in the choir. How many children from the grade do not participate in any of these three clubs?

  Topics:

  Arithmetic Combinatorics Algebra -> Word Problems Set Theory

• Knights of the Round Table

  Around a round table sit 12 knights, each of whom is either an elf or a dwarf. It is known that the number of elves is greater than the number of dwarves. Prove that there are two elves who sit opposite each other.

  Will this continue to be true if the total number of knights is 120?

  Topics:

  Combinatorics -> Pigeonhole Principle Logic -> Reasoning / Logic Proof and Example -> Proof by Contradiction

• Question

  Prove that among five integers, it is possible to choose two whose difference is divisible by `4`.

  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic Combinatorics -> Pigeonhole Principle Number Theory -> Division -> Parity (Even/Odd) Arithmetic -> Division with Remainder

• Question

  a. Prove that among `11` natural numbers, it is always possible to choose two such that their units digit is the same.

  b. Prove that among `11` natural numbers, it is always possible to choose two such that their difference is divisible by `10`.

  Topics:

  Combinatorics -> Pigeonhole Principle Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 5 and 25

• Question

  A total of `21` children have `200` nuts. Prove that there exist two children who have the same number of nuts.

  Topics:

  Combinatorics -> Pigeonhole Principle Proof and Example -> Proof by Contradiction Minimum and Maximum Problems / Optimization Problems

• Question

  There are `30` students in a class. During a test, Pinchas made `13` mistakes, and the rest made fewer mistakes. Prove that there are three students who made the same number of mistakes.

  Topics:

  Combinatorics -> Pigeonhole Principle Logic -> Reasoning / Logic Proof and Example -> Proof by Contradiction Minimum and Maximum Problems / Optimization Problems