Combinatorics

Combinatorics is the art of counting. It deals with selections, arrangements, and combinations of objects. Questions involve determining the number of ways to perform tasks, arrange items (permutations), or choose subsets (combinations), often using principles like the product rule and sum rule.

Pigeonhole Principle Double Counting Binomial Coefficients and Pascal's Triangle Product Rule / Rule of Product Graph Theory Matchings Induction (Mathematical Induction) Game Theory Combinatorial Geometry Invariants Case Analysis / Checking Cases Processes / Procedures Number Tables Colorings

• Question

  A two-digit number is written on the board. Avi claims that the units digit of the number is twice the tens digit. Beni claims that the number is divisible by `9`. Gal claims that the number is divisible by `4`. Dani claims that the number is divisible by `27`. It is known that one of them is wrong, and the rest are correct. What number is written on the board?

  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 2, 4, and 8 Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 3 and 9 Algebra -> Word Problems Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures

• Question

  A square is divided into several convex polygons (more than `1`), each of which has a different number of sides. Prove that among these polygons there is a triangle.

  Topics:

  Combinatorics -> Pigeonhole Principle Combinatorics -> Combinatorial Geometry Combinatorics -> Graph Theory Geometry -> Plane Geometry -> Triangles Proof and Example -> Proof by Contradiction Geometry -> Solid Geometry / Geometry in Space -> Polyhedra Minimum and Maximum Problems / Optimization Problems

• Question

  Is it possible to cut a triangle into four convex shapes: a triangle, a quadrilateral, a pentagon, and a hexagon?

  Topics:

  Geometry -> Plane Geometry -> Triangles Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  In a magical land, there are `2017` cities, and each city is connected by direct roads to at least `1008` other cities. Prove that from any city in the magical land, it is possible to reach any other city (not necessarily by a direct route).

  Topics:

  Combinatorics -> Graph Theory Proof and Example -> Proof by Contradiction

• Question

  How many triangles are there in the image?

  

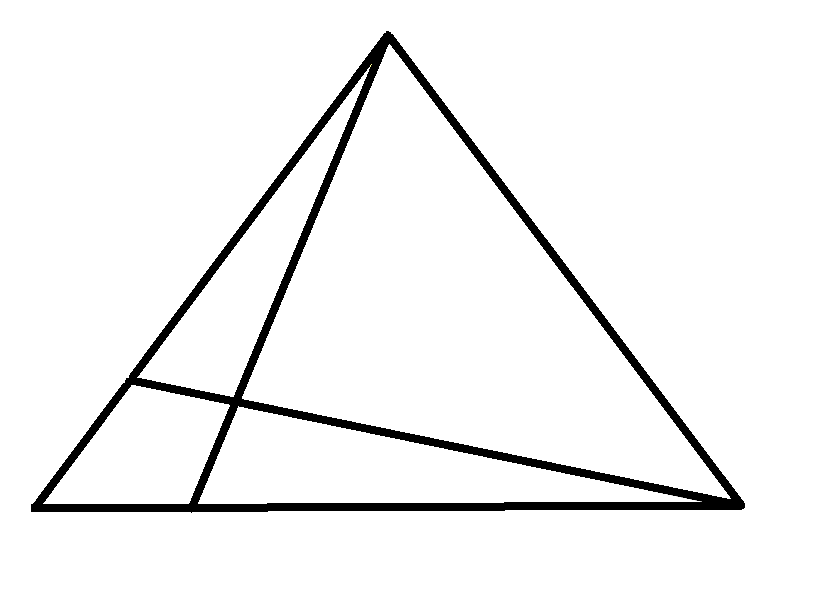  Topics:

  Geometry -> Plane Geometry -> Triangles Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures

• Quarter Yin-Yang

  The shape in the drawing is constructed as follows: Divide the diameter of a semicircle into two equal parts, and construct two additional semicircles on them as diameters: one inwards, and one outwards.

  

  Divide the shape into two congruent parts.

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Cut a square into three parts, and then assemble them into an acute triangle with all sides of different lengths.

  Topics:

  Geometry -> Plane Geometry -> Triangles -> Triangle Congruence Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Given a sheet of paper of size `10×10` cm. Can you cut out a number of circles from this sheet such that the sum of their diameters is greater than `5` meters?

  Topics:

  Arithmetic Geometry -> Area Calculation Proof and Example -> Constructing an Example / Counterexample Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  The following numbers are written on the board: `1, 2, 3, …, 2016, 2017`. In one move, it is allowed to choose a pair of numbers written on the board, erase them, and write their (positive) difference in their place. After several such operations, a single number remains on the board. Is it possible that this is zero?

  Topics:

  Arithmetic Combinatorics -> Invariants Combinatorics -> Induction (Mathematical Induction) Number Theory -> Division -> Parity (Even/Odd) Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Proof and Example -> Proof by Contradiction

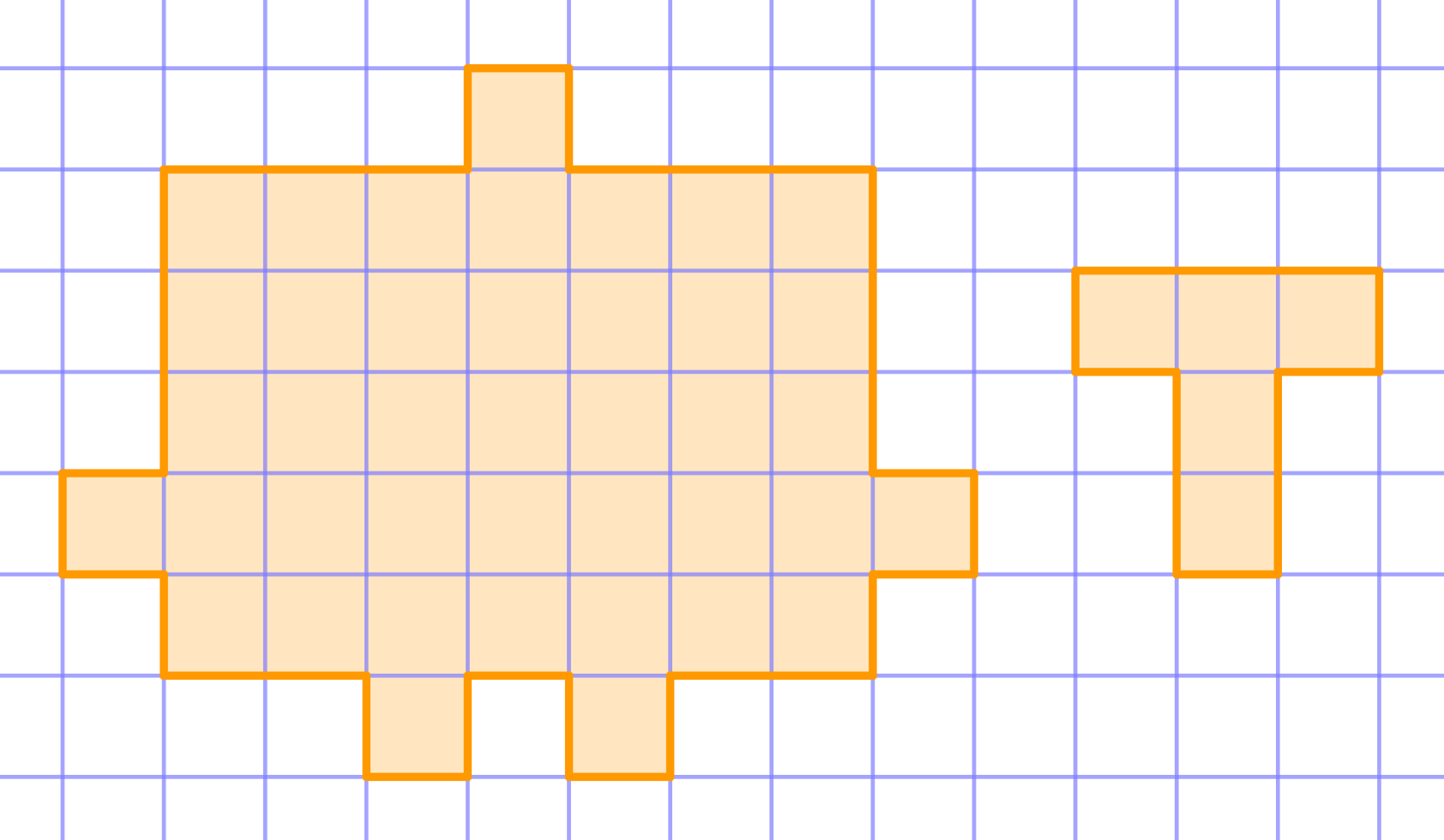
• Question

  Cut the given shape into "T" shapes as shown in the diagram:

  

  Topics:

  Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry