Geometry, Area Calculation

This topic focuses on methods for determining the size of a two-dimensional surface or region. Questions involve calculating the areas of various geometric shapes like triangles, quadrilaterals, circles, and more complex composite figures, often requiring application of specific formulas.

• Question

  In the figure, a semicircle is shown with three circles inscribed within it: the large circle, tangent to the diameter of the semicircle at its center, and two smaller circles on the sides, symmetrically arranged. Which area is larger: the shaded area or the unshaded area?

  

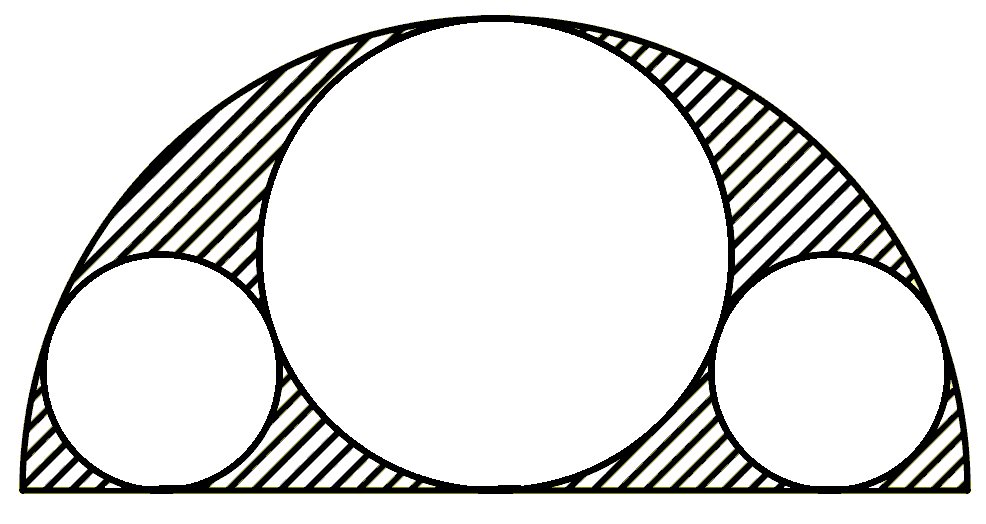  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Symmetry

• Quarter Yin-Yang

  The shape in the drawing is constructed as follows: Divide the diameter of a semicircle into two equal parts, and construct two additional semicircles on them as diameters: one inwards, and one outwards.

  

  Divide the shape into two congruent parts.

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Given a sheet of paper of size `10×10` cm. Can you cut out a number of circles from this sheet such that the sum of their diameters is greater than `5` meters?

  Topics:

  Arithmetic Geometry -> Area Calculation Proof and Example -> Constructing an Example / Counterexample Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  It is known that all the angles of the given shape are right angles. Cut the shape into two polygons of equal area. You are only allowed to use an unmarked ruler.

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Two congruent triangles form a Star of David as depicted in the drawing. Prove that the shaded area is equal to the hatched area.

  

  Show hint

  Log in here to receive the hint
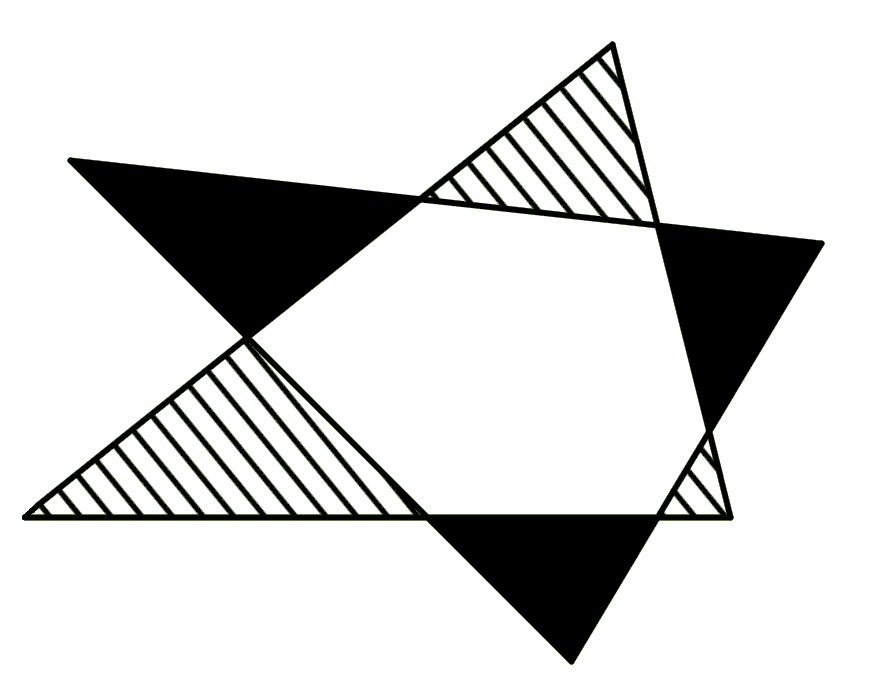  Topics:

  Geometry -> Area Calculation Proof and Example Set Theory Geometry -> Plane Geometry -> Triangles -> Triangle Congruence

• Question

  Can you fit a rectangle of size `5xx5` into a rectangle of size `4xx6`?

  Topics:

  Geometry -> Area Calculation

• Area of the Shape

  Given a grid paper where the area of each square is one unit area. Find the area of the shape (in unit areas)

   

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 3-4 Question 7

• Question

  Inside a square with side length 1, `n>=101` points are marked, such that no three are collinear. A triangle is called marked if its vertices are marked points. Prove that the area of one of the marked triangles is less than `1/100`

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Pigeonhole Principle Combinatorics -> Combinatorial Geometry Geometry -> Plane Geometry Geometry -> Area Calculation
  Sources:
  • Mink Exercises and Additional Competition Materials, 2018-2019, Exercise 4

• Hexagon

  In the diagram, there is a regular hexagon. By what factor is the area of the white region larger than the area of the shaded region?

  (A regular hexagon is a hexagon where all sides are equal and all angles are equal.)

  

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 5-6 Question 6

• Products of Areas

  In the figure, there is a rectangle and a point inside it. Two segments are drawn through the point, parallel to the sides of the rectangle, dividing the rectangle into 4 smaller rectangles.
  Prove that the product of the areas of the shaded rectangles inside the rectangle is equal to the product of the areas of the unshaded rectangles inside the rectangle.

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Algebra -> Equations
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Final, Grades 3-4 Question 4