Geometry, Area Calculation
This topic focuses on methods for determining the size of a two-dimensional surface or region. Questions involve calculating the areas of various geometric shapes like triangles, quadrilaterals, circles, and more complex composite figures, often requiring application of specific formulas.
-
Product of Areas
In the diagram, there is a quadrilateral with perpendicular diagonals. Prove that the product of the areas of the shaded regions within the quadrilateral is equal to the product of the areas of the unshaded regions within the quadrilateral.
Sources: -
Cutting
What is the largest number of rectangles of size `2 times 5` that can be cut from a `9 times 9` square?
Sources: -
Gray Area
In the figure is a rectangle composed of 5 squares of size `2 times 2 ` and a line that intersects it diagonally.
Find the area of the shaded region.
Sources: -
Puzzle
You have a puzzle where each piece looks like this:
The following shape is made up of 12 pieces. What is its perimeter?
Sources: -
Regular Polygons and Circles
A.
In the right-hand figure, there is a square containing 4 circles. The radii of the circles are equal to each other, and each circle is tangent to two other circles and also to two sides of the square. Find the ratio between the area of the blue part and the area of the white part of the square.
B.
In the left-hand figure, there is a hexagon containing 6 circles with the same radius. Each circle is tangent to two other circles and also to one side of the hexagon, at its midpoint. Find the ratio between the area of the blue part and the area of the white part of the hexagon.
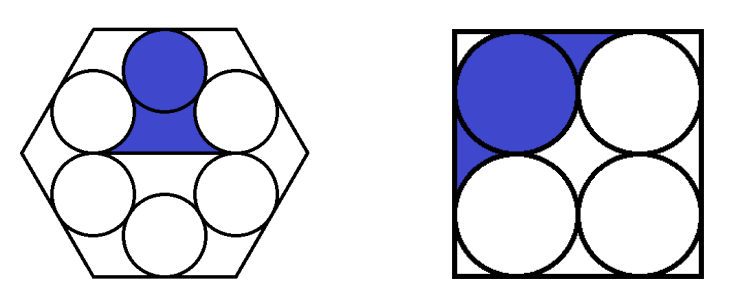
(Solution format: "x, y" for example "1/8, 7/100")
Sources:- Gillis Mathematical Olympiad, 2016-2017 Question 1
-
Right Triangles and a Square
Given a large number of congruent right triangles.
The side lengths of each triangle are 3, 4, and 5.
What is the maximum number of such triangles that can be placed inside a 20×20 square, such that they do not overlap?
Sources:Topics:Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Pythagorean Theorem- Gillis Mathematical Olympiad, 2016-2017 Question 3
-
Another Gray Area
In the figure, a rectangle of size `3 times 5` and a line that crosses it diagonally. Find the shaded area.
Sources: -
The Secret Area
Daniel drew four rectangles whose sides are parallel to each other. The rectangles created four intersection areas (see drawing).
Given the areas of three of the four. Find the area of the fourth intersection.
Sources: -
Hexagon and Triangle
A regular hexagon and an equilateral triangle have the same perimeter. The area of the triangle is known to be 60. Find the area of the hexagon.
Sources: -
Sum of Squares
Given a rectangle with an area of 13 and a perimeter of 20. On two adjacent sides of the rectangle, two squares are constructed, as shown in the figure. Find the sum of the areas of the squares.
Sources:







