Algebra

Algebra is a broad branch of mathematics that uses symbols (usually letters) to represent numbers and to state rules and relationships. It involves manipulating expressions, solving equations and inequalities, and studying functions and structures. Questions cover a wide range of these topics.

Algebraic Techniques Equations Inequalities Word Problems Sequences

• Question

  Is the following number prime? 

  `4^9 + 6^10 + 3^20`

  Topics:

  Number Theory -> Prime Numbers Algebra -> Algebraic Techniques -> Short Multiplication Formulas / Algebraic Identities

• Question

  The distinct real numbers `x` and `y` satisfy the equation:

  `x^2 – 2000x = y^2 – 2000y`

  Find the sum of `x` and `y`.

  Topics:

  Algebra -> Algebraic Techniques -> Short Multiplication Formulas / Algebraic Identities Algebra -> Equations

• Question

  Solve the equation:

  `(x + 2010)(x + 2011)(x + 2012) = (x + 2011)(x + 2012)(x + 2013) `

  Topics:

  Algebra -> Algebraic Techniques Algebra -> Equations Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
  Sources:
  • problems.ru web site

• Question

  Given a cone (with an axis of symmetry in its center, perpendicular to its base) with a height of 6 and a base that is a circle with radius `sqrt2`. A cube is inscribed within the cone – it rests on the cone's base and all its upper vertices touch the cone. Find the side length of the cube. Justify your answer.

  

  Show hint

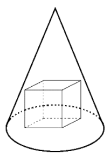  Log in here to receive the hint
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Algebra -> Equations Geometry -> Plane Geometry -> Pythagorean Theorem Geometry -> Plane Geometry -> Triangles -> Triangle Similarity
  Sources:
  • Gillis Mathematical Olympiad, 2015-2016 Question 2

• Question

  Given an `M times N` matrix, where each cell contains a real number. It is known that the sum of the numbers in each row and each column is equal to `1`.

  Prove that `M = N`.

  Topics:

  Combinatorics -> Double Counting Logic -> Reasoning / Logic Algebra -> Inequalities -> Averages / Means

• Question

  Given a positive integer N, consider the following process: Let `S(N)` denote the sum of the digits of N. Take the sum of the digits of `S(N)`. Repeat this operation until a single-digit number is obtained. We call the number of times we performed the above process until we obtained a single-digit number the "depth" of N. For example, the depth of 49 is `S(49)=13 -> S(13)=4`, the operation was performed twice (and the depth of 45 is 1).

  a) Prove that for every number N there is indeed a finite depth, that is, a single-digit number is always obtained at some stage of the process.

  b) Let `x(n)` denote the minimum number (with the smallest value) with depth N. Find the remainder of `x(5776)` when divided by 6. Justify your answer!

  c) Find the remainder of the number `x(5776) - x(5708)` when divided by 2016. Justify your answer!

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic Combinatorics -> Induction (Mathematical Induction) Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence
  Sources:
  • Gillis Mathematical Olympiad, 2015-2016 Question 3

• Question

  Prove that any real number can be written as the sum of 9 numbers, each of which is composed only of the digits 0 and 7.

  Topics:

  Number Theory Arithmetic Proof and Example Algebra -> Sequences
  Sources:
  • Tournament of Towns, 1980-1981, Spring, Main Version, Grades 11-12 Question 3

• Coins and Cakes

  Miriam has coins of two shekels and of five shekels.

  If she pays only with two-shekel coins, she will be 60 shekels short of buying 4 cakes.

  If she pays only with five-shekel coins, she will be 60 shekels short of buying 5 cakes.

  In total, she is 60 shekels short of buying 6 cakes. How much does a cake cost?

  Show hint

  Log in here to receive the hint
  Topics:

  Algebra -> Equations Algebra -> Word Problems
  Sources:
  • Beno Arbel Olympiad, 2013, Grade 7 Question 2

• Question

  How many solutions in natural numbers are there to the equation `(2013 - x)(2013-y)=2013^2`?

  Topics:

  Number Theory -> Prime Numbers -> Prime Factorization Algebra -> Equations -> Diophantine Equations
  Sources:
  • Beno Arbel Olympiad, 2013, Grade 7 Question 6

• Question

  A box contains pencils in three colors: red, green, and blue, totaling `20` pencils. There are `6` times more blue pencils than green pencils. There are fewer red pencils than green pencils. How many red pencils are in the box?

  Topics:

  Arithmetic Algebra -> Inequalities Algebra -> Word Problems Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures