Geometry, Plane Geometry
Plane Geometry concerns figures and shapes on a flat, two-dimensional surface. It covers properties of points, lines, angles, polygons (like triangles and quadrilaterals), and circles. Questions typically involve proofs, constructions, and calculations related to these elements.
Area Calculation Triangles Circles Symmetry Angle Calculation Pythagorean Theorem Triangle Inequality-
THE BETSY ROSS PUZZLE
A correspondent asked me to supply him with the solution to an old puzzle that is attributed to a certain Betsy Ross, of Philadelphia, who showed it to George Washington. It consists in so folding a piece of paper that with one clip of the scissors a five-pointed star of Freedom may be produced. Whether the story of the puzzle's origin is a true one or not I cannot say, but I have a print of the old house in Philadelphia where the lady is said to have lived, and I believe it still stands there. But my readers will doubtless be interested in the little poser.
Take a circular piece of paper and so fold it that with one cut of the scissors you can produce a perfect five-pointed star.
Sources:Topics:Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 161
-
THE PAPER BOX
It may be interesting to introduce here, though it is not strictly a puzzle, an ingenious method for making a paper box.
Take a square of stout paper and by successive foldings make all the creases indicated by the dotted lines in the illustration. Then cut away the eight little triangular pieces that are shaded, and cut through the paper along the dark lines. The second illustration shows the box half folded up, and the reader will have no difficulty in effecting its completion. Before folding up, the reader might cut out the circular piece indicated in the diagram, for a purpose I will now explain.
This box will be found to serve excellently for the production of vortex rings. These rings, which were discussed by Von Helmholtz in `1858`, are most interesting, and the box (with the hole cut out) will produce them to perfection. Fill the box with tobacco smoke by blowing it gently through the hole. Now, if you hold it horizontally, and softly tap the side that is opposite to the hole, an immense number of perfect rings can be produced from one mouthful of smoke. It is best that there should be no currents of air in the room. People often do not realise that these rings are formed in the air when no smoke is used. The smoke only makes them visible. Now, one of these rings, if properly directed on its course, will travel across the room and put out the flame of a candle, and this feat is much more striking if you can manage to do it without the smoke. Of course, with a little practice, the rings may be blown from the mouth, but the box produces them in much greater perfection, and no skill whatever is required. Lord Kelvin propounded the theory that matter may consist of vortex rings in a fluid that fills all space, and by a development of the hypothesis he was able to explain chemical combination.
Sources: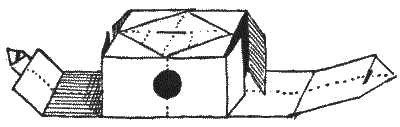
- Amusements in Mathematics, Henry Ernest Dudeney Question 163
-
THE POTATO PUZZLE
Take a circular slice of potato, place it on the table, and see into how large a number of pieces you can divide it with six cuts of a knife. Of course you must not readjust the pieces or pile them after a cut. What is the greatest number of pieces you can make? The illustration shows how to make sixteen pieces. This can, of course, be easily beaten.
Sources:Topics:Geometry -> Plane Geometry Algebra -> Sequences Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
The illustration shows how to make sixteen pieces. This can, of course, be easily beaten.
Sources:Topics:Geometry -> Plane Geometry Algebra -> Sequences Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 164
-
THE SEVEN PIGS

Here is a little puzzle that was put to one of the sons of Erin the other day and perplexed him unduly, for it is really quite easy. It will be seen from the illustration that he was shown a sketch of a square pen containing seven pigs. He was asked how he would intersect the pen with three straight fences so as to enclose every pig in a separate sty. In other words, all you have to do is to take your pencil and, with three straight strokes across the square, enclose each pig separately. Nothing could be simpler.
The Irishman complained that the pigs would not keep still while he was putting up the fences. He said that they would all flock together, or one obstinate beast would go into a corner and flock all by himself. It was pointed out to him that for the purposes of the puzzle the pigs were stationary. He answered that Irish pigs are not stationery—they are pork. Being persuaded to make the attempt, he drew three lines, one of which cut through a pig. When it was explained that this is not allowed, he protested that a pig was no use until you cut its throat. "Begorra, if it's bacon ye want without cutting your pig, it will be all gammon." We will not do the Irishman the injustice of suggesting that the miserable pun was intentional. However, he failed to solve the puzzle. Can you do it?
Sources:Topics:Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 165
-
THE LANDOWNER'S FENCES
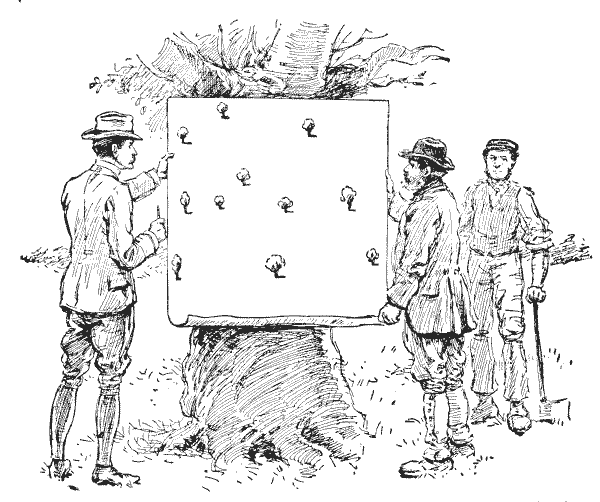 The landowner in the illustration is consulting with his bailiff over a rather puzzling little question. He has a large plan of one of his fields, in which there are eleven trees. Now, he wants to divide the field into just eleven enclosures by means of straight fences, so that every enclosure shall contain one tree as a shelter for his cattle. How is he to do it with as few fences as possible? Take your pencil and draw straight lines across the field until you have marked off the eleven enclosures (and no more), and then see how many fences you require. Of course the fences may cross one another.
Sources:Topics:Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
The landowner in the illustration is consulting with his bailiff over a rather puzzling little question. He has a large plan of one of his fields, in which there are eleven trees. Now, he wants to divide the field into just eleven enclosures by means of straight fences, so that every enclosure shall contain one tree as a shelter for his cattle. How is he to do it with as few fences as possible? Take your pencil and draw straight lines across the field until you have marked off the eleven enclosures (and no more), and then see how many fences you require. Of course the fences may cross one another.
Sources:Topics:Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 166
-
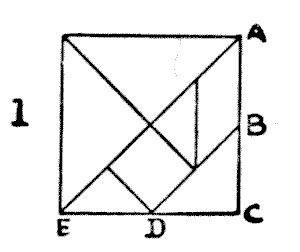
A TANGRAM PARADOX
Many pastimes of great antiquity, such as chess, have so developed and changed down the centuries that their original inventors would scarcely recognize them. This is not the case with Tangrams, a recreation that appears to be at least four thousand years old, that has apparently never been dormant, and that has not been altered or "improved upon" since the legendary Chinaman Tan first cut out the seven pieces shown in Diagram I. If you mark the point B, midway between A and C, on one side of a square of any size, and D, midway between C and E, on an adjoining side, the direction of the cuts is too obvious to need further explanation. Every design in this article is built up from the seven pieces of blackened cardboard. It will at once be understood that the possible combinations are infinite.
The late Mr. Sam Loyd, of New York, who published a small book of very ingenious designs, possessed the manuscripts of the late Mr. Challenor, who made a long and close study of Tangrams. This gentleman, it is said, records that there were originally seven books of Tangrams, compiled in China two thousand years before the Christian era. These books are so rare that, after forty years' residence in the country, he only succeeded in seeing perfect copies of the first and seventh volumes with fragments of the second. Portions of one of the books, printed in gold leaf upon parchment, were found in Peking by an English soldier and sold for three hundred pounds.
A few years ago a little book came into my possession, from the library of the late Lewis Carroll, entitled The Fashionable Chinese Puzzle. It contains three hundred and twenty-three Tangram designs, mostly nondescript geometrical figures, to be constructed from the seven pieces. It was "Published by J. and E. Wallis, `42` Skinner Street, and J. Wallis, Jun., Marine Library, Sidmouth" (South Devon). There is no date, but the following note fixes the time of publication pretty closely: "This ingenious contrivance has for some time past been the favourite amusement of the ex-Emperor Napoleon, who, being now in a debilitated state and living very retired, passes many hours a day in thus exercising his patience and ingenuity." The reader will find, as did the great exile, that much amusement, not wholly uninstructive, may be derived from forming the designs of others. He will find many of the illustrations to this article quite easy to build up, and some rather difficult. Every picture may thus be regarded as a puzzle.
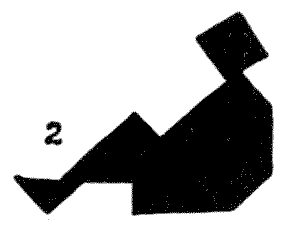
But it is another pastime altogether to create new and original designs of a pictorial character, and it is surprising what extraordinary scope the Tangrams afford for producing pictures of real life—angular and often grotesque, it is true, but full of character. I give an example of a recumbent figure (`2`) that is particularly graceful, and only needs some slight reduction of its angularities to produce an entirely satisfactory outline.
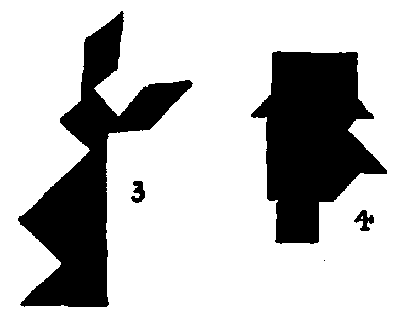
As I have referred to the author of Alice in Wonderland, I give also my designs of the March Hare (`3`) and the Hatter (`4`). I also give an attempt at Napoleon (`5`), and a very excellent Red Indian with his Squaw by Mr. Loyd (`6` and `7`). A large number of other designs will be found in an article by me in The Strand Magazine for November, `1908`.

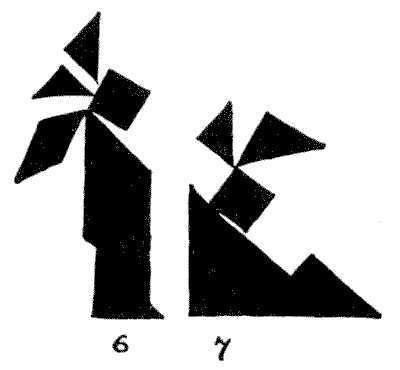
On the appearance of this magazine article, the late Sir James Murray, the eminent philologist, tried, with that amazing industry that characterized all his work, to trace the word "tangram" to its source. At length he wrote as follows:—"One of my sons is a professor in the Anglo-Chinese college at Tientsin. Through him, his colleagues, and his students, I was able to make inquiries as to the alleged Tan among Chinese scholars. Our Chinese professor here (Oxford) also took an interest in the matter and obtained information from the secretary of the Chinese Legation in London, who is a very eminent representative of the Chinese literati."
"The result has been to show that the man Tan, the god Tan, and the 'Book of Tan' are entirely unknown to Chinese literature, history, or tradition. By most of the learned men the name, or allegation of the existence, of these had never been heard of. The puzzle is, of course, well known. It is called in Chinese ch'i ch'iao t'u; literally, 'seven-ingenious-plan' or 'ingenious-puzzle figure of seven pieces.' No name approaching 'tangram,' or even 'tan,' occurs in Chinese, and the only suggestions for the latter were the Chinese t'an, 'to extend'; or t'ang, Cantonese dialect for 'Chinese.' It was suggested that probably some American or Englishman who knew a little Chinese or Cantonese, wanting a name for the puzzle, might concoct one out of one of these words and the European ending 'gram.' I should say the name 'tangram' was probably invented by an American some little time before `1864` and after `1847`, but I cannot find it in print before the `1864` edition of Webster. I have therefore had to deal very shortly with the word in the dictionary, telling what it is applied to and what conjectures or guesses have been made at the name, and giving a few quotations, one from your own article, which has enabled me to make more of the subject than I could otherwise have done."
Several correspondents have informed me that they possess, or had possessed, specimens of the old Chinese books. An American gentleman writes to me as follows:—"I have in my possession a book made of tissue paper, printed in black (with a Chinese inscription on the front page), containing over three hundred designs, which belongs to the box of 'tangrams,' which I also own. The blocks are seven in number, made of mother-of-pearl, highly polished and finely engraved on either side. These are contained in a rosewood box `2` `1/8` in. square. My great uncle, ——, was one of the first missionaries to visit China. This box and book, along with quite a collection of other relics, were sent to my grandfather and descended to myself."

My correspondent kindly supplied me with rubbings of the Tangrams, from which it is clear that they are cut in the exact proportions that I have indicated. I reproduce the Chinese inscription (`8`) for this reason. The owner of the book informs me that he has submitted it to a number of Chinamen in the United States and offered as much as a dollar for a translation. But they all steadfastly refused to read the words, offering the lame excuse that the inscription is Japanese. Natives of Japan, however, insist that it is Chinese. Is there something occult and esoteric about Tangrams, that it is so difficult to lift the veil? Perhaps this page will come under the eye of some reader acquainted with the Chinese language, who will supply the required translation, which may, or may not, throw a little light on this curious question.

By using several sets of Tangrams at the same time we may construct more ambitious pictures. I was advised by a friend not to send my picture, "A Game of Billiards" (`9`), to the Academy. He assured me that it would not be accepted because the "judges are so hide-bound by convention." Perhaps he was right, and it will be more appreciated by Post-impressionists and Cubists. The players are considering a very delicate stroke at the top of the table. Of course, the two men, the table, and the clock are formed from four sets of Tangrams. My second picture is named "The Orchestra" (`10`), and it was designed for the decoration of a large hall of music. Here we have the conductor, the pianist, the fat little cornet-player, the left-handed player of the double-bass, whose attitude is life-like, though he does stand at an unusual distance from his instrument, and the drummer-boy, with his imposing music-stand. The dog at the back of the pianoforte is not howling: he is an appreciative listener.


One remarkable thing about these Tangram pictures is that they suggest to the imagination such a lot that is not really there. Who, for example, can look for a few minutes at Lady Belinda (`11`) and the Dutch girl (`12`) without soon feeling the haughty expression in the one case and the arch look in the other? Then look again at the stork (`13`), and see how it is suggested to the mind that the leg is actually much more slender than any one of the pieces employed. It is really an optical illusion. Again, notice in the case of the yacht (`14`) how, by leaving that little angular point at the top, a complete mast is suggested. If you place your Tangrams together on white paper so that they do not quite touch one another, in some cases the effect is improved by the white lines; in other cases it is almost destroyed.
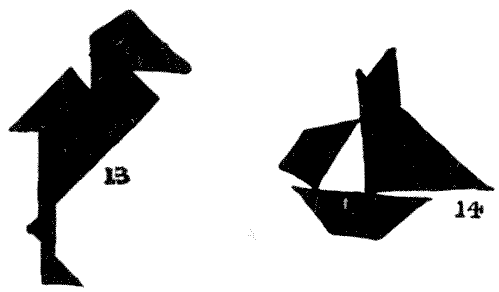
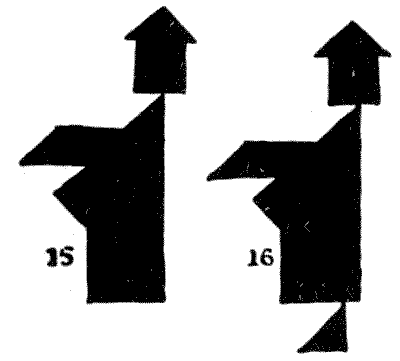
Finally, I give an example from the many curious paradoxes that one happens upon in manipulating Tangrams. I show designs of two dignified individuals (`15` and `16`) who appear to be exactly alike, except for the fact that one has a foot and the other has not. Now, both of these figures are made from the same seven Tangrams. Where does the second man get his foot from?
 Sources:Topics:Geometry -> Plane Geometry Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
Sources:Topics:Geometry -> Plane Geometry Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 169
-
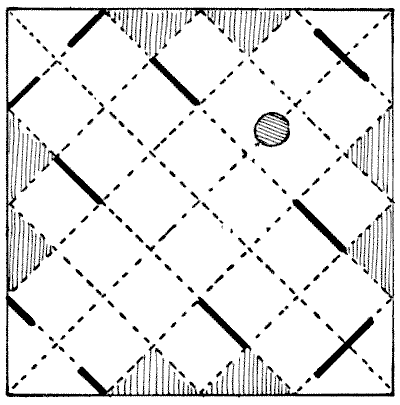
THE CUSHION COVERS
The above represents a square of brocade. A lady wishes to cut it in four pieces so that two pieces will form one perfectly square cushion top, and the remaining two pieces another square cushion top. How is she to do it? Of course, she can only cut along the lines that divide the twenty-five squares, and the pattern must "match" properly without any irregularity whatever in the design of the material. There is only one way of doing it. Can you find it?
Sources:Topics:Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 170
-
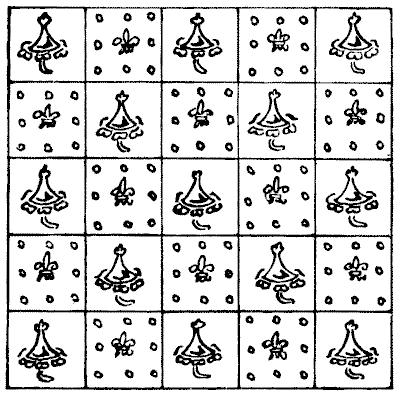
MRS. PERKINS'S QUILT
 It will be seen that in this case the square patchwork quilt is built up of `169` pieces. The puzzle is to find the smallest possible number of square portions of which the quilt could be composed and show how they might be joined together. Or, to put it the reverse way, divide the quilt into as few square portions as possible by merely cutting the stitches.
Sources:Topics:Geometry -> Plane Geometry Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
It will be seen that in this case the square patchwork quilt is built up of `169` pieces. The puzzle is to find the smallest possible number of square portions of which the quilt could be composed and show how they might be joined together. Or, to put it the reverse way, divide the quilt into as few square portions as possible by merely cutting the stitches.
Sources:Topics:Geometry -> Plane Geometry Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 173
-
ANOTHER PATCHWORK PUZZLE
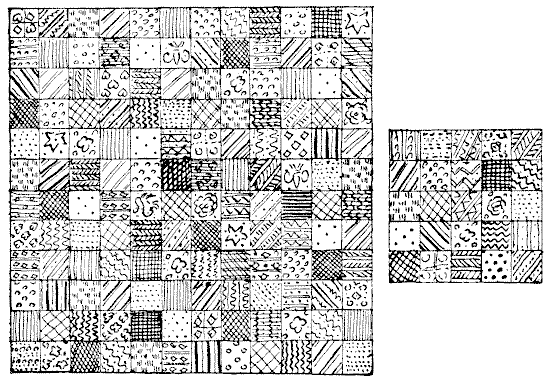 A lady was presented, by two of her girl friends, with the pretty pieces of silk patchwork shown in our illustration. It will be seen that both pieces are made up of squares all of the same size—one 12x12 and the other 5x5. She proposes to join them together and make one square patchwork quilt, 13x13, but, of course, she will not cut any of the material—merely cut the stitches where necessary and join together again. What perplexes her is this. A friend assures her that there need be no more than four pieces in all to join up for the new quilt. Could you show her how this little needlework puzzle is to be solved in so few pieces?
Sources:Topics:Geometry -> Plane Geometry Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
A lady was presented, by two of her girl friends, with the pretty pieces of silk patchwork shown in our illustration. It will be seen that both pieces are made up of squares all of the same size—one 12x12 and the other 5x5. She proposes to join them together and make one square patchwork quilt, 13x13, but, of course, she will not cut any of the material—merely cut the stitches where necessary and join together again. What perplexes her is this. A friend assures her that there need be no more than four pieces in all to join up for the new quilt. Could you show her how this little needlework puzzle is to be solved in so few pieces?
Sources:Topics:Geometry -> Plane Geometry Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 175
-
ANOTHER LINOLEUM PUZZLE
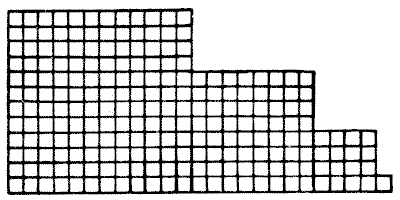
Can you cut this piece of linoleum into four pieces that will fit together and form a perfect square? Of course the cuts may only be made along the lines.
Sources:Topics:Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 177