Geometry, Plane Geometry
Plane Geometry concerns figures and shapes on a flat, two-dimensional surface. It covers properties of points, lines, angles, polygons (like triangles and quadrilaterals), and circles. Questions typically involve proofs, constructions, and calculations related to these elements.
Area Calculation Triangles Circles Symmetry Angle Calculation Pythagorean Theorem Triangle Inequality-
Question
In the figure, a semicircle is shown with three circles inscribed within it: the large circle, tangent to the diameter of the semicircle at its center, and two smaller circles on the sides, symmetrically arranged. Which area is larger: the shaded area or the unshaded area?
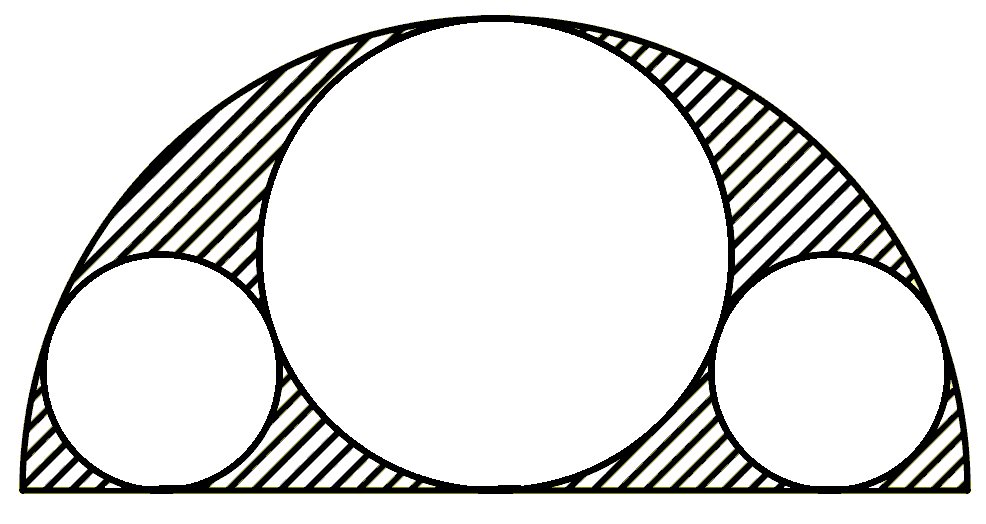Topics:Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Symmetry -
Quarter Yin-Yang
The shape in the drawing is constructed as follows: Divide the diameter of a semicircle into two equal parts, and construct two additional semicircles on them as diameters: one inwards, and one outwards.
Divide the shape into two congruent parts.
Topics:Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems -
Question
In a quadrilateral, the lengths of all diagonals and all sides are less than 1. Prove that the quadrilateral can be covered by a circle with a radius of 0.9.
Sources: -
Regular Polygons and Circles
A.
In the right-hand figure, there is a square containing 4 circles. The radii of the circles are equal to each other, and each circle is tangent to two other circles and also to two sides of the square. Find the ratio between the area of the blue part and the area of the white part of the square.
B.
In the left-hand figure, there is a hexagon containing 6 circles with the same radius. Each circle is tangent to two other circles and also to one side of the hexagon, at its midpoint. Find the ratio between the area of the blue part and the area of the white part of the hexagon.
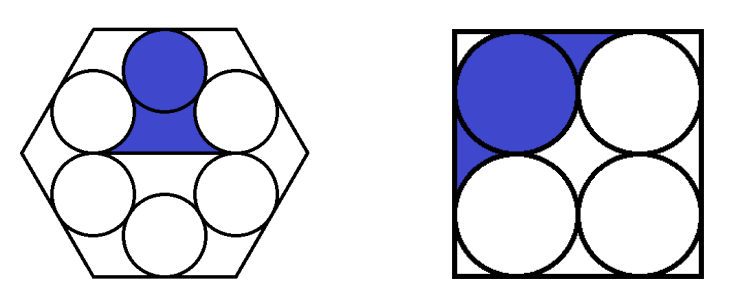
(Solution format: "x, y" for example "1/8, 7/100")
Sources:- Gillis Mathematical Olympiad, 2016-2017 Question 1
-
Area of the Shape
In the image, the area of the semicircle is equal to 1. Find the area of the larger shape, given that all the curved lines in the image are quarter circles.
Sources:
-
Cyclic Quadrilaterals
Given two triangles ACE, BDF
intersecting at 6 points: G,H,I,J,K,L
as shown in the figure. It is given that in each of the quadrilaterals
EFGI, DELH, CDKG, BCJL, ABIK a circle can be inscribed.
Is it possible that a circle can also be inscribed in quadrilateral FAHJ?
Sources:Topics:Geometry -> Solid Geometry / Geometry in Space Geometry -> Plane Geometry -> Circles Algebra -> Equations Algebra -> Inequalities Proof and Example -> Proof by Contradiction Geometry -> Plane Geometry -> Angle Calculation- Gillis Mathematical Olympiad, 2019-2020 Question 5
-
Sets in the Plane
A. Does there exist a set A in the plane such that its intersection with every circle contains exactly two points?
B. Does there exist a set B in the plane such that its intersection with every circle of radius 1 contains exactly two points?
Sources:Topics:Geometry -> Plane Geometry -> Circles Proof and Example -> Constructing an Example / Counterexample Set Theory Proof and Example -> Proof by Contradiction Minimum and Maximum Problems / Optimization Problems- Grossman Math Olympiad, 2006 Question 3
-
How a Wheel Turns
All 6 wheels in the diagram rotate as they touch each other without slipping. The diameter of the leftmost wheel is 15.7 cm and it makes 12 revolutions per minute.
It is known that the smallest wheel makes one revolution per second.
What is the diameter of the smallest wheel?
Sources:
-
DEFECTIVE OBSERVATION
Our observation of little things is frequently defective, and our memories very liable to lapse. A certain judge recently remarked in a case that he had no recollection whatever of putting the wedding-ring on his wife's finger. Can you correctly answer these questions without having the coins in sight? On which side of a penny is the date given? Some people are so unobservant that, although they are handling the coin nearly every day of their lives, they are at a loss to answer this simple question. If I lay a penny flat on the table, how many other pennies can I place around it, every one also lying flat on the table, so that they all touch the first one? The geometrician will, of course, give the answer at once, and not need to make any experiment. He will also know that, since all circles are similar, the same answer will necessarily apply to any coin. The next question is a most interesting one to ask a company, each person writing down his answer on a slip of paper, so that no one shall be helped by the answers of others. What is the greatest number of three-penny-pieces that may be laid flat on the surface of a half-crown, so that no piece lies on another or overlaps the surface of the half-crown? It is amazing what a variety of different answers one gets to this question. Very few people will be found to give the correct number. Of course the answer must be given without looking at the coins. Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 28
-
THE SPOT ON THE TABLE
A boy, recently home from school, wished to give his father an exhibition of his precocity. He pushed a large circular table into the corner of the room, as shown in the illustration, so that it touched both walls, and he then pointed to a spot of ink on the extreme edge.
"Here is a little puzzle for you, pater," said the youth. "That spot is exactly eight inches from one wall and nine inches from the other. Can you tell me the diameter of the table without measuring it?"
The boy was overheard to tell a friend, "It fairly beat the guv'nor;" but his father is known to have remarked to a City acquaintance that he solved the thing in his head in a minute. I often wonder which spoke the truth.
Sources:Topics:Geometry -> Plane Geometry -> Circles Algebra -> Equations Algebra -> Word Problems Geometry -> Plane Geometry -> Pythagorean Theorem- Amusements in Mathematics, Henry Ernest Dudeney Question 97