Geometry, Plane Geometry

Plane Geometry concerns figures and shapes on a flat, two-dimensional surface. It covers properties of points, lines, angles, polygons (like triangles and quadrilaterals), and circles. Questions typically involve proofs, constructions, and calculations related to these elements.

Area Calculation Triangles Circles Symmetry Angle Calculation Pythagorean Theorem Triangle Inequality

• Hexagonal Tiling

  Given two types of tiles. The shape of each tile of the first type is a regular hexagon with a side of length 1. The shape of each tile of the second type is a regular hexagon with a side of length 2. An unlimited supply of tiles of each type is given. Is it possible to tile the entire plane using these tiles, using both types of tiles?

  Topics:

  Logic -> Reasoning / Logic Proof and Example -> Proof by Contradiction Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Grossman Math Olympiad, 2006 Question 4

• THE RAILWAY STATION CLOCK

  A clock hangs on the wall of a railway station, `71` ft. `9` in. long and `10` ft. `4` in. high. Those are the dimensions of the wall, not of the clock! While waiting for a train we noticed that the hands of the clock were pointing in opposite directions, and were parallel to one of the diagonals of the wall. What was the exact time?
  Topics:

  Algebra -> Word Problems Arithmetic -> Fractions Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 65

• THE YACHT RACE

  Now then, ye land-lubbers, hoist your baby-jib-topsails, break out your spinnakers, ease off your balloon sheets, and get your head-sails set!

  Our race consists in starting from the point at which the yacht is lying in the illustration and touching every one of the sixty-four buoys in fourteen straight courses, returning in the final tack to the buoy from which we start. The seventh course must finish at the buoy from which a flag is flying.

  This puzzle will call for a lot of skilful seamanship on account of the sharp angles at which it will occasionally be necessary to tack. The point of a lead pencil and a good nautical eye are all the outfit that we require.  

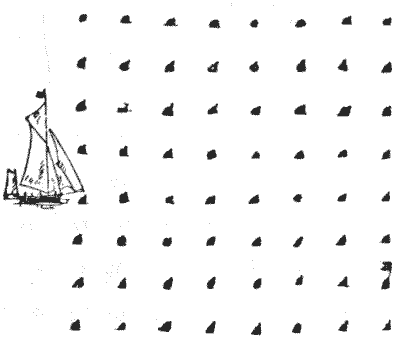
  This is difficult, because of the condition as to the flag-buoy, and because it is a re-entrant tour. But again we are allowed those oblique lines.

  Topics:

  Geometry -> Plane Geometry -> Angle Calculation Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 330

• Question

  Cut a square into three parts, and then assemble them into an acute triangle with all sides of different lengths.

  Topics:

  Geometry -> Plane Geometry -> Triangles -> Triangle Congruence Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Two congruent triangles form a Star of David as depicted in the drawing. Prove that the shaded area is equal to the hatched area.

  

  Show hint

  Log in here to receive the hint
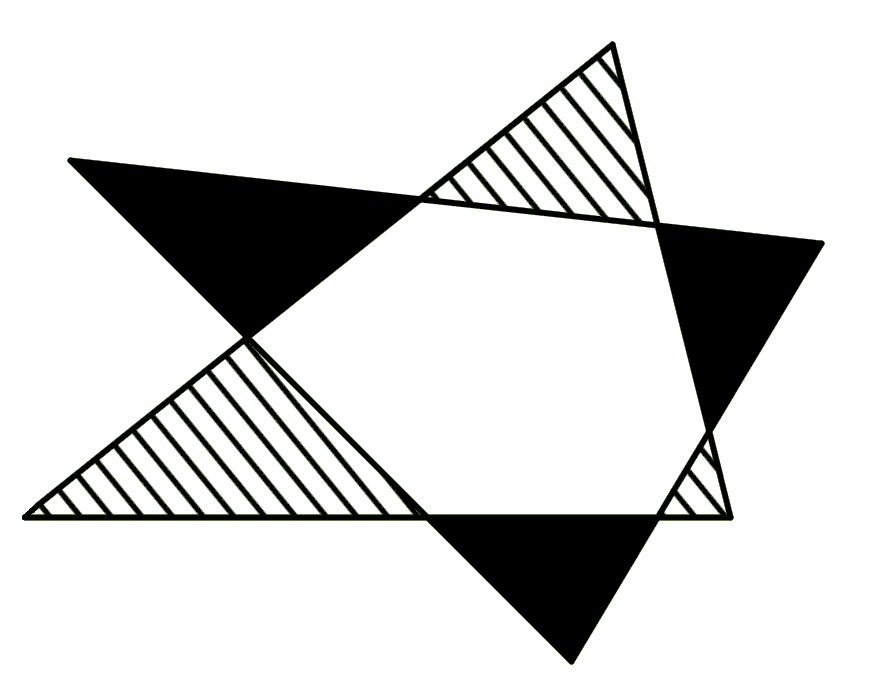  Topics:

  Geometry -> Area Calculation Proof and Example Set Theory Geometry -> Plane Geometry -> Triangles -> Triangle Congruence

• Question

  Consider an arbitrary triangle. Draw tangents to the inscribed circle parallel to the sides of the triangle. These tangents cut off three smaller triangles from the original triangle. Prove that the sum of the radii of the inscribed circles of these smaller triangles is equal to the radius of the inscribed circle of the original triangle.

  Topics:

  Geometry -> Plane Geometry -> Circles -> Tangent to a Circle Geometry -> Plane Geometry -> Triangles -> Triangle Similarity

• A Walk in the Plane

  Given a Cartesian coordinate system x-y in the plane. You need to get from the point (1,0) to the point (2006,2005), where in each step you are allowed to move one unit up (in the positive direction of y) or one unit to the right (in the positive direction of the x-axis).

  a. In how many different paths can the task be performed?

  b. In how many different paths can the task be performed if it is forbidden at any stage to pass through a point on the line x=y?

  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Binomial Coefficients and Pascal's Triangle Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Reflection
  Sources:
  • Grossman Math Olympiad, 2006 Question 7

• THE MILKMAID PUZZLE

  Here is a little pastoral puzzle that the reader may, at first sight, be led into supposing is very profound, involving deep calculations. He may even say that it is quite impossible to give any answer unless we are told something definite as to the distances. And yet it is really quite "childlike and bland."

   

  In the corner of a field is seen a milkmaid milking a cow, and on the other side of the field is the dairy where the extract has to be deposited. But it has been noticed that the young woman always goes down to the river with her pail before returning to the dairy. Here the suspicious reader will perhaps ask why she pays these visits to the river. I can only reply that it is no business of ours. The alleged milk is entirely for local consumption.

  "Where are you going to, my pretty maid?"
  "Down to the river, sir," she said.
  "I'll not choose your dairy, my pretty maid."
  "Nobody axed you, sir," she said.

  
  If one had any curiosity in the matter, such an independent spirit would entirely disarm one. So we will pass from the point of commercial morality to the subject of the puzzle.

  Draw a line from the milking-stool down to the river and thence to the door of the dairy, which shall indicate the shortest possible route for the milkmaid. That is all. It is quite easy to indicate the exact spot on the bank of the river to which she should direct her steps if she wants as short a walk as possible. Can you find that spot?

  Topics:

  Minimum and Maximum Problems / Optimization Problems Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Reflection
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 187