Combinatorics, Case Analysis / Checking Cases, Processes / Procedures

This category covers problems involving sequences of operations or steps that evolve over time or iterations. Questions might ask about the outcome of a process, whether it terminates, or properties of its state after a certain number of steps. Often related to algorithms or invariants.

• Question

  How many triangles are there in the image?

  

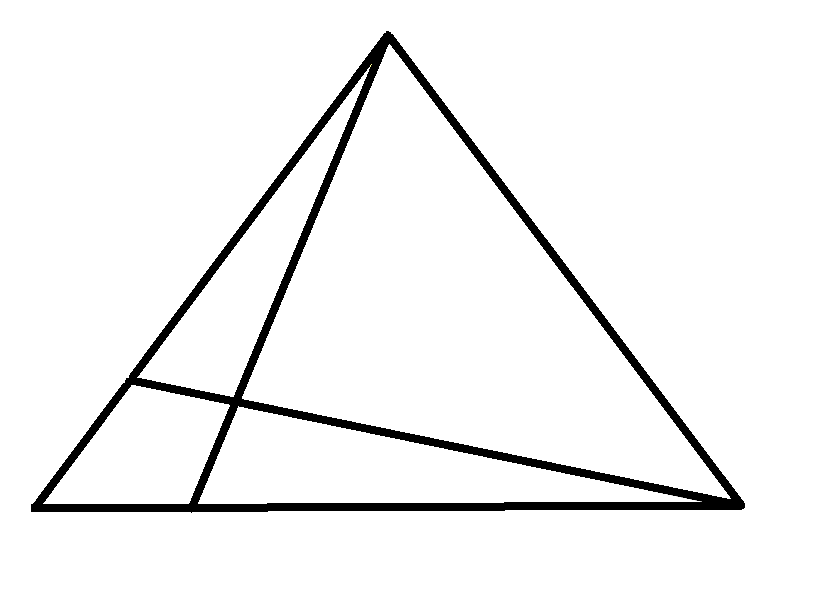  Topics:

  Geometry -> Plane Geometry -> Triangles Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures

• Question

  The following numbers are written on the board: `1, 2, 3, …, 2016, 2017`. In one move, it is allowed to choose a pair of numbers written on the board, erase them, and write their (positive) difference in their place. After several such operations, a single number remains on the board. Is it possible that this is zero?

  Topics:

  Arithmetic Combinatorics -> Invariants Combinatorics -> Induction (Mathematical Induction) Number Theory -> Division -> Parity (Even/Odd) Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Proof and Example -> Proof by Contradiction

• 26 Coins

  Given `26` coins that look identical. One of the coins is counterfeit, and it weighs less than a regular coin. How can you find the counterfeit coin using three weighings on a balance scale without weights?

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Induction (Mathematical Induction) Logic -> Reasoning / Logic Algorithm Theory -> Weighing Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Minimum and Maximum Problems / Optimization Problems

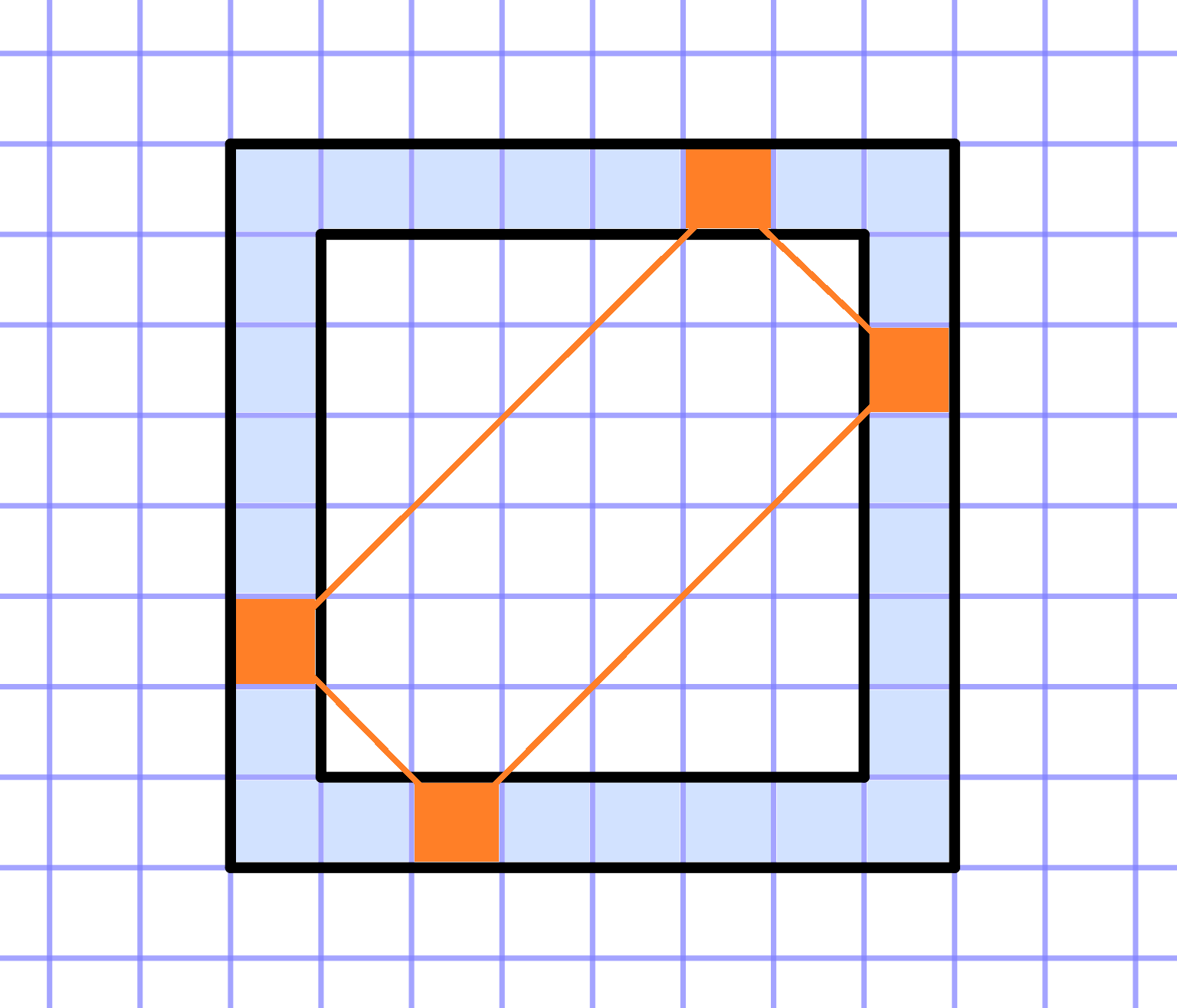
• Frame

  On a grid paper, a square of size `NxxN` is given. Consider its frame with a width of one square. It consists of `4*(N-1)` squares.

  Can you write `4*(N-1)` consecutive integers (not necessarily positive) in the squares of the frame, such that the following condition holds:

  For every rectangle whose vertices are on the frame and whose sides are parallel to the diagonals of the original square, the sum of the numbers at the vertices is equal to a constant value. This also includes the "degenerate" rectangles of zero width that coincide with the diagonals of the square - in this case, simply sum the two numbers at the opposite vertices of the square.

  For:

  a. `N=3`

  b. `N=4`

  c. `N=5`

  

  Topics:

  Arithmetic Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Constructing an Example / Counterexample Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
  Sources:
  • Tournament of Towns, 1983-1984, Fall, Practice Version, Grades 9-10 Question 3 Points 2+3+4

• Question

  A. You have a large jug of 12 liters of olive oil and two empty smaller vessels, one of 5 liters and one of 8 liters. Can you divide the oil you have into two equal parts, if you only have these vessels and no additional measuring tools?

  B. The same question, but instead of the 5-liter vessel, you have a 4-liter vessel.

  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules Combinatorics -> Invariants Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Constructing an Example / Counterexample Number Theory -> Greatest Common Divisor (GCD) and Least Common Multiple (LCM) -> Euclidean Algorithm Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Proof and Example -> Proof by Contradiction

• Question

  A bouquet is composed of `7` roses, white and red (both colors are present). It is known that out of every two roses, one is necessarily white. How many white roses and how many red roses are in the bouquet?

  Topics:

  Combinatorics -> Pigeonhole Principle Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures

• Question

  Does there exist a perfect square that ends with the digits `...2017`?

  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic Number Theory -> Division -> Parity (Even/Odd) Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Proof and Example -> Proof by Contradiction

• Question

  What is the maximum number of chess kings that can be placed on an `8xx8` board such that they do not threaten each other?

  Topics:

  Combinatorics -> Pigeonhole Principle Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

• Question

  In the following arithmetic puzzle, different digits have been replaced by different letters, and identical digits – by identical letters. Reconstruct the puzzle:

  `BAOxxBAxxB=2002`

  Topics:

  Arithmetic Algebra -> Equations Algebra -> Inequalities Logic -> Reasoning / Logic Number Theory -> Prime Numbers -> Prime Factorization Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic

• Question

  Given `50` distinct natural numbers between `1` and `100`. It is known that no two of these numbers sum to `100`. Is it necessarily true that one of these numbers must be a perfect square?

  Topics:

  Number Theory -> Prime Numbers Arithmetic Combinatorics -> Pigeonhole Principle Combinatorics -> Matchings Logic -> Reasoning / Logic Proof and Example -> Constructing an Example / Counterexample Set Theory Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Proof and Example -> Proof by Contradiction