גאומטריה, גאומטריה במישור, מעגלים
נושא זה מכסה את תכונות המעגלים, כולל רדיוס, קוטר, היקף, שטח, מיתרים, משיקים, חותכים, קשתות וגזרות. שאלות כוללות חישובים הקשורים לאלמנטים אלו והבנת משפטים על זוויות וקטעים במעגלים.
משיק למעגל-
שני פרסות הסוס
מדוע יש להתייחס לפרסות סוס כאל "מזל" הוא אחד מאותם דברים שאף אדם לא יכול להבין. זוהי אמונה טפלה עתיקה מאוד, וג'ון אוברי (`1626-1700`) אומר, "לרוב הבתים בווסט אנד של לונדון יש פרסת סוס על סף הדלת." ברחוב מונמות' היו שבע עשרה בשנת `1813` ושבע עד לשנת `1855`. אפילו לורד נלסון מסמר אחת לתורן של הספינה ויקטורי. כיום אנו מוצאים שזה יותר מועיל ל"מזל טוב" לוודא שהם ממוסמרים היטב על רגלי הסוס שאנו עומדים לנסוע בו.
אף על פי כן, עד כמה שהפרסה, כמו הצלב קרס וסמלים אחרים שיצא לי לעסוק בהם מדי פעם, שימשה לסמל בריאות, שגשוג ורצון טוב כלפי בני אדם, אנו יכולים להתייחס אליה בכבוד מסוים. האם ייתכן שיש איזשהו מסתורין מתמטי איזוטרי או אבוד החבוי בצורת פרסת סוס? בחנתי את הנושא הזה, ואני רוצה להסב את תשומת לבם של הקוראים שלי לעובדה המדהימה ביותר שזוג פרסות הסוס המוצגות באיור שלי קשורות בצורה בולטת ויפה לעיגול, שהוא הסמל של הנצח. אני מציג את העובדה הזו בצורה של בעיה פשוטה, כדי שניתן יהיה לראות עד כמה הקשר הזה הוסתר בצורה מתוחכמת במשך עידנים רבים. הקוראים שלי ישמחו, אני יודע, כשהם ימצאו את המפתח למסתורין.
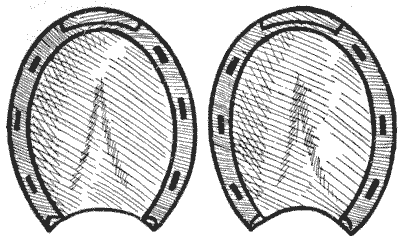
גזרו בזהירות את שתי פרסות הסוס מסביב לקו המתאר ואז חתכו אותן לארבעה חלקים, שכולם שונים בצורתם, שיתאימו זה לזה וייצרו מעגל מושלם. כל נעל חייבת להיחתך לשני חלקים וכל החלק בטלף הסוס הכלול בתוך קו המתאר ישמש וייחשב כחלק מהשטח.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 160
-
החתולים של הקוסם
 קוסם הניח עשרה חתולים בתוך מעגל קסם כפי שמוצג באיור שלנו, והפנט אותם כך שיישארו נייחים במהלך רצונו. לאחר מכן הוא הציע לצייר שלושה מעגלים בתוך המעגל הגדול, כך שאף חתול לא יוכל להתקרב לחתול אחר מבלי לחצות מעגל קסם. נסו לצייר את שלושת המעגלים כך שלכל חתול תהיה מתחם משלו ולא יוכל להגיע לחתול אחר מבלי לחצות קו.
מקורות:
קוסם הניח עשרה חתולים בתוך מעגל קסם כפי שמוצג באיור שלנו, והפנט אותם כך שיישארו נייחים במהלך רצונו. לאחר מכן הוא הציע לצייר שלושה מעגלים בתוך המעגל הגדול, כך שאף חתול לא יוכל להתקרב לחתול אחר מבלי לחצות מעגל קסם. נסו לצייר את שלושת המעגלים כך שלכל חתול תהיה מתחם משלו ולא יוכל להגיע לחתול אחר מבלי לחצות קו.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 167
-
חידת הגינה
פרופסור רַאקְבְּרֵיין סיפר לי שעישן לאחרונה מקטרת ידידותית מתחת לעץ בגינה של מכר כפרי. הגינה הייתה מוקפת בארבעה קירות ישרים, וידידו הודיע לו שהוא מדד אותם ומצא שאורכם הוא `80, 45, 100`, ו-`63` יארד בהתאמה. "אם כך," אמר הפרופסור, "נוכל לחשב את השטח המדויק של הגינה." "זה בלתי אפשרי," השיב המארח שלו, "כי אתה יכול לקבל מספר אינסופי של צורות שונות עם ארבעת הצדדים האלה." "אבל אתה שוכח," אמר רַאקְבְּרֵיין, עם ניצוץ בעיניו, "שאמרת לי פעם ששתלת את העץ הזה במרחק שווה מכל ארבע פינות הגינה." האם תוכלו לחשב את שטח הגינה?מקורות:נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים אלגברה -> משוואות אלגברה -> בעיות מילוליות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 182
-
ציור ספירלה
אם תחזיקו את הדף אופקית ותסובבו אותו במהירות תוך כדי התבוננות במרכז הספירלה, היא תיראה כאילו היא מסתובבת. ייתכן שקוראים רבים מכירים את האשליה האופטית הקטנה הזו. אבל החידה היא להראות כיצד הצלחתי לצייר את הספירלה הזו בדיוק כה רב מבלי להשתמש בדבר מלבד זוג מחוגות ודף הנייר שעליו נעשה הדיאגרמה. איך הייתם פועלים בנסיבות כאלה?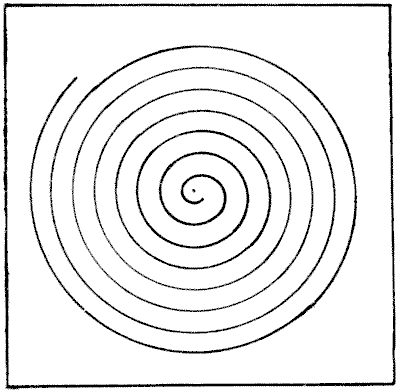 מקורות:נושאים:גאומטריה -> גאומטריה במישור -> מעגלים
מקורות:נושאים:גאומטריה -> גאומטריה במישור -> מעגלים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 183
-
חידת הירח
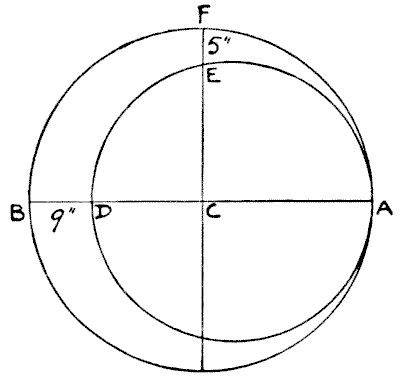 הנה חידה גיאומטרית קלה. הירח נוצר על ידי שני מעגלים, ו-C הוא מרכז המעגל הגדול יותר. רוחב הירח בין B ל-D הוא `9` אינץ', ובין E ל-F הוא `5` אינץ'. מהם הקטרים של שני המעגלים?
מקורות:
הנה חידה גיאומטרית קלה. הירח נוצר על ידי שני מעגלים, ו-C הוא מרכז המעגל הגדול יותר. רוחב הירח בין B ל-D הוא `9` אינץ', ובין E ל-F הוא `5` אינץ'. מהם הקטרים של שני המעגלים?
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 191
-
חומות הגן
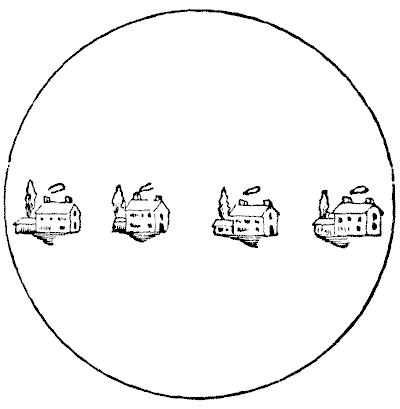
יזם נדל"ן ספקולטיבי מחזיק בשדה עגול, עליו הקים ארבעה קוטג'ים, כפי שמוצג באיור. השדה מוקף בחומה מלבנים, והבעלים התחייב להקים עוד שלושה קירות לבנים, כך שהשכנים לא יוכלו להציץ אחד לשני, אך ארבעת הדיירים מתעקשים שלא תהיה אפליה, ושלכל אחד יהיה בדיוק אותו אורך שטח קיר לעצי הפרי שלו. החידה היא להראות כיצד ניתן לבנות את שלושת הקירות כך שלכל דייר יהיה אותו שטח אדמה, ובדיוק אותו אורך של קיר.
כמובן, כל גן חייב להיות סגור לחלוטין על ידי קירותיו, וחייב להיות אפשרי להוכיח שלכל גן יש בדיוק אותו אורך של קיר. אם החידה נפתרת כראוי, אין צורך במספרים.
מקורות:נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 194
-
חידת המַחְגֵּלִים
זה משונה איך תנאי או מגבלה נוספים יכולים לפעמים להפוך חידה קלה באופן אבסורדי לחידה מעניינת ואולי קשה. אני זוכר שקניתי ברחוב לפני שנים רבות חידה מכנית קטנה שנמכרה בצורה אדירה באותה תקופה. היא כללה מדליה עם חורים, והחידה הייתה להעביר טבעת עם רווח מחור לחור עד שהיא ניתקה סופית. כשהלכתי ברחוב, מהר מאוד רכשתי את הטריק להסיר את הטבעת ביד אחת תוך כדי החזקת החידה בכיס. חבר שהראיתי לו את הפעלול הקטן ניגש להשיג זאת בעצמו, וכשפגשתי אותו כמה ימים לאחר מכן הוא הציג את מומחיותו באומנות. אבל הוא הופתע קצת כשלקחתי ממנו את החידה ואז, תוך כדי החזקת המדליה בין האצבע לאגודל של יד אחת, בסדרה של טלטלות ונענועים קטנים גרמתי לטבעת, בלי שאגע בה אפילו, ליפול על הרצפה. הבוחן הקטן הבא כנראה יתברר כאגוז קשה לפיצוח עבור קוראים רבים, פשוט בגלל התנאים המוגבלים:—
הראו כיצד למצוא בדיוק את אמצעו של כל קו ישר באמצעות מַחְגֵּלִים בלבד. אסור להשתמש בשום סרגל, עיפרון או חפץ אחר—רק במַחְגֵּלִים; ולא יתאפשר שום טריק או התחמקות, כמו קיפול הנייר. אתם חייבים פשוט להשתמש במַחְגֵּלִים בצורה רגילה ולגיטימית.
מקורות:נושאים:גאומטריה -> גאומטריה במישור -> מעגלים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 197
-
בעניין גלגלים
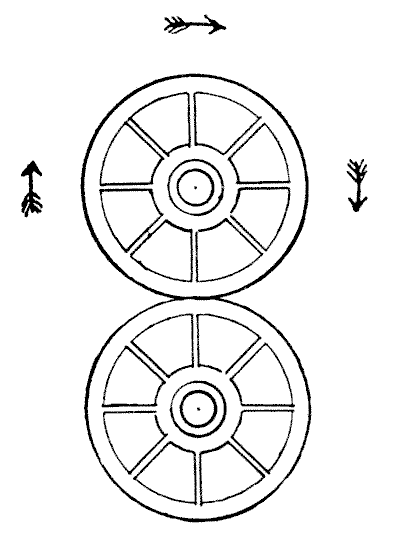
ישנן מספר עובדות מוזרות הנוגעות לתנועת גלגלים אשר עשויות לבלבל את המתחילים. לדוגמה: כאשר רכבת נוסעת מלונדון לקרו, חלקים מסוימים ברכבת, בכל רגע נתון, נעים למעשה מקרו לכיוון לונדון. האם תוכלו לציין את החלקים האלה? זה נראה אבסורדי שחלקים מאותה רכבת יכולים בכל זמן נתון לנוע בכיוונים מנוגדים, אך כך הם פני הדברים.
באיור המצורף יש לנו שני גלגלים. הגלגל התחתון אמור להיות קבוע והגלגל העליון מסתובב סביבו בכיוון החצים. עכשיו, כמה פעמים הגלגל העליון מסתובב סביב צירו שלו במהלך סיבוב שלם סביב הגלגל השני? אל תמהרו עם התשובה, אחרת כמעט בטוח שתטעו. נסו זאת עם שני מטבעות על השולחן והתשובה הנכונה תפתיע אתכם, כשתצליחו לראות אותה.
מקורות:נושאים:גאומטריה -> גאומטריה במישור -> מעגלים גאומטריה -> גאומטריה במישור -> העתקות של מישור -> העתקות חפיפה (איזומטריות) -> סיבוב- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 203
-
הנחת מטבעות חצי פני
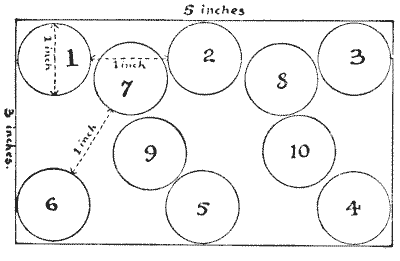 הנה חידה קטנה ומעניינת שהוצעה לי על ידי מר וו. טי. וויט. סמנו על דף נייר שטח מלבני של `5` אינץ' על `3` אינץ', ואז מצאו את המספר הגדול ביותר של מטבעות חצי פני שניתן להניח בתוך המתחם בתנאים הבאים. קוטר של מטבע חצי פני הוא בדיוק אינץ' אחד. הניחו את מטבע חצי הפני הראשון שלכם היכן שתרצו, ואז הניחו את המטבע השני בדיוק במרחק של אינץ' אחד מהראשון, את השלישי במרחק של אינץ' אחד מהשני, וכן הלאה. אסור לאף מטבע חצי פני לגעת במטבע אחר או לחצות את הגבול. האיור שלנו יבהיר את העניין בצורה מושלמת. מטבע מספר `2` נמצא במרחק אינץ' אחד ממספר `1`; מספר `3` במרחק אינץ' אחד ממספר `2`; מספר `4` במרחק אינץ' אחד ממספר `3`; אבל אחרי שמניחים את מספר `10`, איננו יכולים להתקדם בניסיון זה. עם זאת, אפשר היה להכניס עוד כמה מטבעות חצי פני. כמה יכול הקורא להניח?
מקורות:
הנה חידה קטנה ומעניינת שהוצעה לי על ידי מר וו. טי. וויט. סמנו על דף נייר שטח מלבני של `5` אינץ' על `3` אינץ', ואז מצאו את המספר הגדול ביותר של מטבעות חצי פני שניתן להניח בתוך המתחם בתנאים הבאים. קוטר של מטבע חצי פני הוא בדיוק אינץ' אחד. הניחו את מטבע חצי הפני הראשון שלכם היכן שתרצו, ואז הניחו את המטבע השני בדיוק במרחק של אינץ' אחד מהראשון, את השלישי במרחק של אינץ' אחד מהשני, וכן הלאה. אסור לאף מטבע חצי פני לגעת במטבע אחר או לחצות את הגבול. האיור שלנו יבהיר את העניין בצורה מושלמת. מטבע מספר `2` נמצא במרחק אינץ' אחד ממספר `1`; מספר `3` במרחק אינץ' אחד ממספר `2`; מספר `4` במרחק אינץ' אחד ממספר `3`; אבל אחרי שמניחים את מספר `10`, איננו יכולים להתקדם בניסיון זה. עם זאת, אפשר היה להכניס עוד כמה מטבעות חצי פני. כמה יכול הקורא להניח?
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 429
-
שאלה
משולש שרירותי מעבירים משיקים למעגל החסום, במקביל לצלעות המשולש. המשיקים האלה חותכים מהמשולש המקורי שלושה משולשים קטנים. הוכיחו כי סכום הרדיוסים של המעגלים החסומים במשולשים האלה שווה לרדיוס המעגל החסום במשולש המקורי.
נושאים:גאומטריה -> גאומטריה במישור -> מעגלים -> משיק למעגל גאומטריה -> גאומטריה במישור -> משולשים -> דמיון משולשים