Geometry

Geometry is the branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogues. Expected questions involve calculating lengths, angles, areas, and volumes of various shapes, understanding geometric theorems, and solving problems related to spatial reasoning.

Solid Geometry / Geometry in Space Trigonometry Spherical Geometry Plane Geometry Vectors

• THE TWELVE MINCE-PIES

  It will be seen in our illustration how twelve mince-pies may be placed on the table so as to form six straight rows with four pies in every row. The puzzle is to remove only four of them to new positions so that there shall be seven straight rows with four in every row. Which four would you remove, and where would you replace them?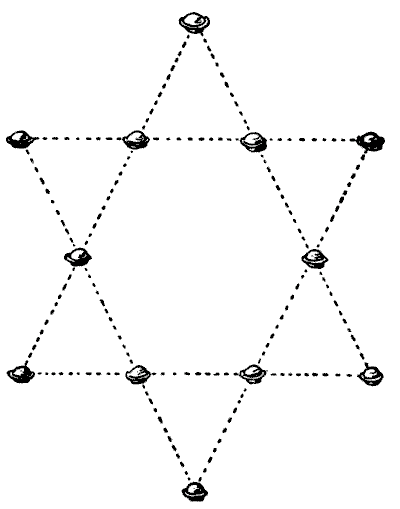
  Topics:

  Combinatorics -> Combinatorial Geometry Geometry -> Plane Geometry
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 211

• A CHESSBOARD FALLACY

   

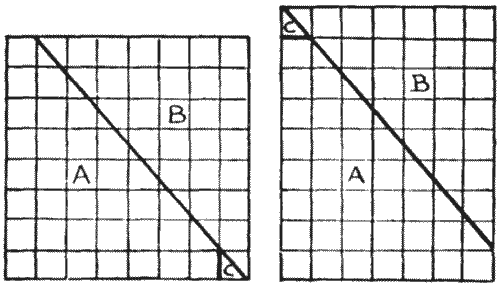
  "Here is a diagram of a chessboard," he said. "You see there are sixty-four squares—eight by eight. Now I draw a straight line from the top left-hand corner, where the first and second squares meet, to the bottom right-hand corner. I cut along this line with the scissors, slide up the piece that I have marked B, and then clip off the little corner C by a cut along the first upright line. This little piece will exactly fit into its place at the top, and we now have an oblong with seven squares on one side and nine squares on the other. There are, therefore, now only sixty-three squares, because seven multiplied by nine makes sixty-three. Where on earth does that lost square go to? I have tried over and over again to catch the little beggar, but he always eludes me. For the life of me I cannot discover where he hides himself."

  "It seems to be like the other old chessboard fallacy, and perhaps the explanation is the same," said Reginald—"that the pieces do not exactly fit."

  "But they do fit," said Uncle John. "Try it, and you will see."

  Later in the evening Reginald and George, were seen in a corner with their heads together, trying to catch that elusive little square, and it is only fair to record that before they retired for the night they succeeded in securing their prey, though some others of the company failed to see it when captured. Can the reader solve the little mystery?

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 413

• Question

  Samuel wants to tile a room measuring `3` by `4` meters using square tiles with a side length of `25` centimeters. How many tiles does Samuel need?

  Topics:

  Arithmetic Geometry -> Area Calculation Algebra -> Word Problems Units of Measurement

• Question

  Let ABCD be a convex quadrilateral inscribed in a circle such that its diagonals are perpendicular to each other. Let O be the center of the circle. Prove that the broken line AOC divides the quadrilateral into two parts of equal area. 
  V. Varvarkin 

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Tournament of Towns, 1980-1981, Spring, Main Version, Grades 9-10 Question 3 Points 5

• Area and Perimeter

  By what percentage will the area of a square increase if its perimeter increases by `10%`?

  Topics:

  Geometry -> Area Calculation Arithmetic -> Percentages

• Stack of Papers

  Several identical rectangular sheets of paper lie on a table. It is known that the top sheet covers more than half the area of every other sheet. Is it necessarily possible to stick a pin into the table that will go through all these sheets?

  Topics:

  Combinatorics -> Pigeonhole Principle Combinatorics -> Combinatorial Geometry Geometry -> Area Calculation Geometry -> Plane Geometry -> Symmetry

• Question

  Semicircles are constructed on the legs and hypotenuse of a right-angled triangle, as shown in the figure. Which area is larger—the hatched area or the shaded area?

  

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Pythagorean Theorem

• Question

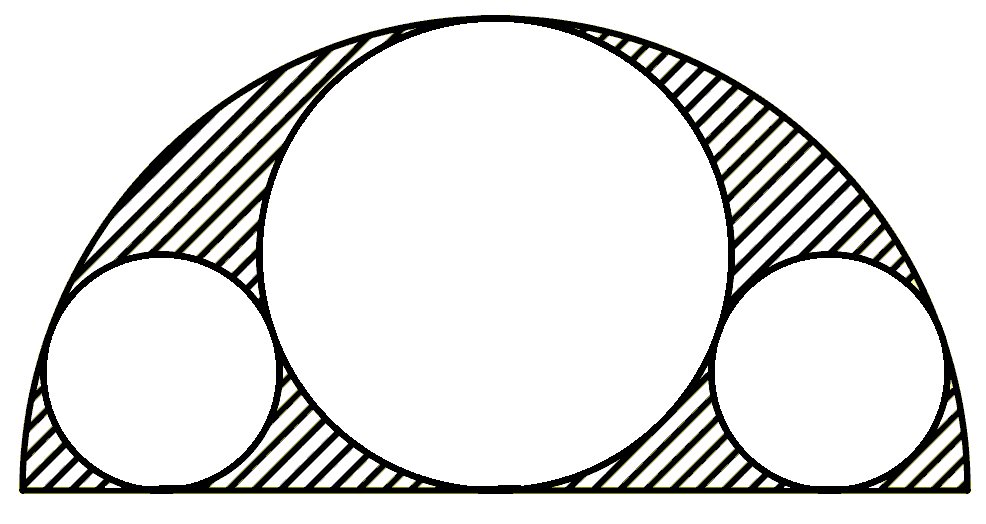
  In the figure, a semicircle is shown with three circles inscribed within it: the large circle, tangent to the diameter of the semicircle at its center, and two smaller circles on the sides, symmetrically arranged. Which area is larger: the shaded area or the unshaded area?

  

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Symmetry

• Quarter Yin-Yang

  The shape in the drawing is constructed as follows: Divide the diameter of a semicircle into two equal parts, and construct two additional semicircles on them as diameters: one inwards, and one outwards.

  

  Divide the shape into two congruent parts.

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Given a sheet of paper of size `10×10` cm. Can you cut out a number of circles from this sheet such that the sum of their diameters is greater than `5` meters?

  Topics:

  Arithmetic Geometry -> Area Calculation Proof and Example -> Constructing an Example / Counterexample Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems