Geometry

Geometry is the branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogues. Expected questions involve calculating lengths, angles, areas, and volumes of various shapes, understanding geometric theorems, and solving problems related to spatial reasoning.

Solid Geometry / Geometry in Space Trigonometry Spherical Geometry Plane Geometry Vectors

• Question

  Given a regular polygon with n vertices. Calculate the number of distinct (non-congruent) triangles whose vertices coincide with the vertices of the polygon.

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules Geometry -> Plane Geometry -> Angle Calculation Geometry -> Plane Geometry -> Triangles -> Triangle Congruence
  Sources:
  • Mink Exercises and Additional Competition Materials, 2018-2019, Exercise 4 Question 3

• Question

  Given an infinite grid whose vertices are colored with two colors, blue and red. Prove that there exist two horizontal lines and two vertical lines such that their four intersection points are colored with the same color.

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Pigeonhole Principle Combinatorics -> Combinatorial Geometry Geometry -> Plane Geometry Combinatorics -> Colorings
  Sources:
  • Zebra Exercises, 2018-2019, Exercise 1 Question 1

• Hexagon

  In the diagram, there is a regular hexagon. By what factor is the area of the white region larger than the area of the shaded region?

  (A regular hexagon is a hexagon where all sides are equal and all angles are equal.)

  

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 5-6 Question 6

• Products of Areas

  In the figure, there is a rectangle and a point inside it. Two segments are drawn through the point, parallel to the sides of the rectangle, dividing the rectangle into 4 smaller rectangles.
  Prove that the product of the areas of the shaded rectangles inside the rectangle is equal to the product of the areas of the unshaded rectangles inside the rectangle.

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Algebra -> Equations
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Final, Grades 3-4 Question 4

• Product of Areas

  In the diagram, there is a quadrilateral with perpendicular diagonals. Prove that the product of the areas of the shaded regions within the quadrilateral is equal to the product of the areas of the unshaded regions within the quadrilateral.

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Final, Grades 5-6 Question 3

• Cutting

  What is the largest number of rectangles of size `2 times 5`  that can be cut from a `9 times 9` square?

  Topics:

  Geometry -> Area Calculation Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Stage A, Grades 3-4 Question 1
  • Young Mathematician Olympiad, 2018-2019, Stage A, Grades 5-6 Question 1

• Gray Area

  In the figure is a rectangle composed of 5 squares of size `2 times 2 ` and a line that intersects it diagonally.
  Find the area of the shaded region.

  

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Symmetry
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Stage A, Grades 3-4 Question 3

• Puzzle

  You have a puzzle where each piece looks like this:

  

  
  The following shape is made up of 12 pieces. What is its perimeter?

  

  Topics:

  Arithmetic Geometry -> Plane Geometry Geometry -> Area Calculation Algebra -> Word Problems
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Stage A, Grades 3-4 Question 6

• Regular Polygons and Circles

  A.

  In the right-hand figure, there is a square containing 4 circles. The radii of the circles are equal to each other, and each circle is tangent to two other circles and also to two sides of the square. Find the ratio between the area of the blue part and the area of the white part of the square.

  B.

  In the left-hand figure, there is a hexagon containing 6 circles with the same radius. Each circle is tangent to two other circles and also to one side of the hexagon, at its midpoint. Find the ratio between the area of the blue part and the area of the white part of the hexagon.

   

  

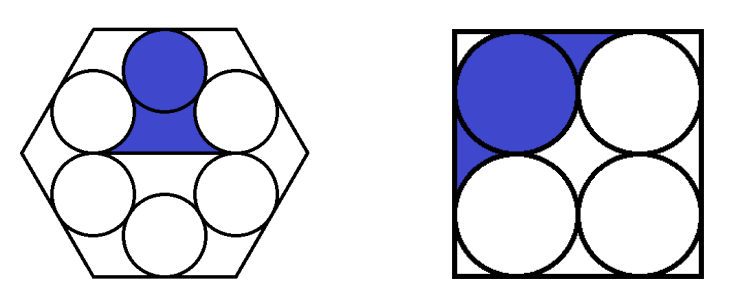
  (Solution format: "x, y" for example "1/8, 7/100")

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles
  Sources:
  • Gillis Mathematical Olympiad, 2016-2017 Question 1

• Right Triangles and a Square

  Given a large number of congruent right triangles.

  The side lengths of each triangle are 3, 4, and 5.

  What is the maximum number of such triangles that can be placed inside a 20×20 square, such that they do not overlap?

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Pythagorean Theorem
  Sources:
  • Gillis Mathematical Olympiad, 2016-2017 Question 3