Geometry

Geometry is the branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogues. Expected questions involve calculating lengths, angles, areas, and volumes of various shapes, understanding geometric theorems, and solving problems related to spatial reasoning.

• Question

  Someone made `15` point-like holes in a carpet that is `4xx4` meters in size. Is it always possible to cut out a rug of size `1xx1` meter from the original carpet such that it has no holes?

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry Combinatorics -> Pigeonhole Principle Combinatorics -> Combinatorial Geometry
  Sources:
  • problems.ru web site

• Question

  On a circle, `2016` blue points and one red point are marked. Consider all possible polygons whose vertices are at these points. Which polygons are more numerous – those that contain the red point or those whose vertices are all blue?

  Topics:

  Combinatorics -> Matchings Geometry -> Plane Geometry -> Circles
  Sources:
  • problems.ru web site

• Area and Perimeter

  By what percentage will the area of a square increase if its perimeter increases by `10%`?

  Topics:

  Geometry -> Area Calculation Arithmetic -> Percentages

• Question

  Suppose two pyramids are tangent to each other if they have no common interior points and they intersect in a non-degenerate planar polygon. Is it possible for 8 pyramids in space to all be tangent to each other? 
  A. Angeles 

  Topics:

  Combinatorics -> Combinatorial Geometry Proof and Example -> Constructing an Example / Counterexample Geometry -> Solid Geometry / Geometry in Space -> Polyhedra
  Sources:
  • Tournament of Towns, 1980-1981, Spring, Main Version, Grades 11-12 Question 1 Points 7

• Question

  Given a cone (with an axis of symmetry in its center, perpendicular to its base) with a height of 6 and a base that is a circle with radius `sqrt2`. A cube is inscribed within the cone – it rests on the cone's base and all its upper vertices touch the cone. Find the side length of the cube. Justify your answer.

  

  Show hint

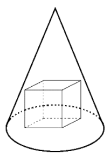  Log in here to receive the hint
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Algebra -> Equations Geometry -> Plane Geometry -> Pythagorean Theorem Geometry -> Plane Geometry -> Triangles -> Triangle Similarity
  Sources:
  • Gillis Mathematical Olympiad, 2015-2016 Question 2

• Question

  The numbers `1`, `2`, `3`, ..., `8` are written on the vertices of a cube. Prove that there exists an edge of the cube such that the difference between the numbers at its endpoints is at least `3`.

  Topics:

  Geometry -> Solid Geometry / Geometry in Space Combinatorics -> Pigeonhole Principle Combinatorics -> Graph Theory Logic -> Reasoning / Logic Proof and Example -> Proof by Contradiction

• Question

  The game takes place on an infinite plane. One player moves the wolf, and another player moves K sheep. After the wolf's move, one of the sheep makes a move, then the wolf again, and so on. In one move, the wolf or a sheep cannot move more than one meter in any direction. Can the wolf always catch at least one sheep, regardless of the initial positions?

  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Invariants Geometry -> Plane Geometry Logic -> Reasoning / Logic Proof and Example -> Constructing an Example / Counterexample Minimum and Maximum Problems / Optimization Problems
  Sources:
  • Tournament of Towns, 1980-1981, Spring, Main Version, Grades 11-12 Question 2

• Question

  Given a line `l` and two points `A, B` at different distances from the line. Find the point `C` on the line such that the difference between the lengths of the segments `AC`, `AB` is maximal.

  Topics:

  Geometry -> Plane Geometry -> Triangle Inequality Minimum and Maximum Problems / Optimization Problems
  Sources:
  • Beno Arbel Olympiad, 2013, Grade 7 Question 3

• 5 Degrees on a Clock

  At what time is there a 5-degree angle between the clock hands?

  Topics:

  Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Beno Arbel Olympiad, 2013, Grade 7 Question 5

• Question

  Does there exist a convex quadrilateral such that each of its diagonals divides it into two acute triangles?

  Topics:

  Proof and Example -> Proof by Contradiction Geometry -> Plane Geometry -> Angle Calculation