Combinatorics, Combinatorial Geometry
Combinatorial Geometry explores the connections between combinatorics and geometry. It deals with problems about arrangements, configurations, and properties of discrete geometric objects (points, lines, polygons). Questions often involve counting, existence proofs, and geometric inequalities.
Cut a Shape / Dissection Problems Grid Paper Geometry / Lattice Geometry-
A Walk in the Plane
Given a Cartesian coordinate system x-y in the plane. You need to get from the point (1,0) to the point (2006,2005), where in each step you are allowed to move one unit up (in the positive direction of y) or one unit to the right (in the positive direction of the x-axis).
a. In how many different paths can the task be performed?
b. In how many different paths can the task be performed if it is forbidden at any stage to pass through a point on the line x=y?
Sources:Topics:Combinatorics -> Combinatorial Geometry Combinatorics -> Binomial Coefficients and Pascal's Triangle Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Reflection- Grossman Math Olympiad, 2006 Question 7
-
Question
There are 5778 extinguished lamps arranged at equal distances on a circle. Below each lamp is a button. Pressing a button changes the state of 4 lamps: the lamp next to the button, the next two lamps in the circle clockwise, and the lamp opposite the button (an extinguished lamp lights up when its state is changed, and a lit lamp is extinguished). What is the maximum number of lamps that can be lit simultaneously?
 Sources:Topics:Combinatorics -> Combinatorial Geometry Combinatorics -> Invariants Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Colorings
Sources:Topics:Combinatorics -> Combinatorial Geometry Combinatorics -> Invariants Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Colorings- Beno Arbel Olympiad, 2017, Grade 8 Question 8
-
THE WIZARD'S CATS
 A wizard placed ten cats inside a magic circle as shown in our illustration, and hypnotized them so that they should remain stationary during his pleasure. He then proposed to draw three circles inside the large one, so that no cat could approach another cat without crossing a magic circle. Try to draw the three circles so that every cat has its own enclosure and cannot reach another cat without crossing a line.
Sources:
A wizard placed ten cats inside a magic circle as shown in our illustration, and hypnotized them so that they should remain stationary during his pleasure. He then proposed to draw three circles inside the large one, so that no cat could approach another cat without crossing a magic circle. Try to draw the three circles so that every cat has its own enclosure and cannot reach another cat without crossing a line.
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 167
-
THE KING AND THE CASTLES
There was once, in ancient times, a powerful king, who had eccentric ideas on the subject of military architecture. He held that there was great strength and economy in symmetrical forms, and always cited the example of the bees, who construct their combs in perfect hexagonal cells, to prove that he had nature to support him. He resolved to build ten new castles in his country all to be connected by fortified walls, which should form five lines with four castles in every line. The royal architect presented his preliminary plan in the form I have shown. But the monarch pointed out that every castle could be approached from the outside, and commanded that the plan should be so modified that as many castles as possible should be free from attack from the outside, and could only be reached by crossing the fortified walls. The architect replied that he thought it impossible so to arrange them that even one castle, which the king proposed to use as a royal residence, could be so protected, but his majesty soon enlightened him by pointing out how it might be done. How would you have built the ten castles and fortifications so as best to fulfil the king's requirements? Remember that they must form five straight lines with four castles in every line.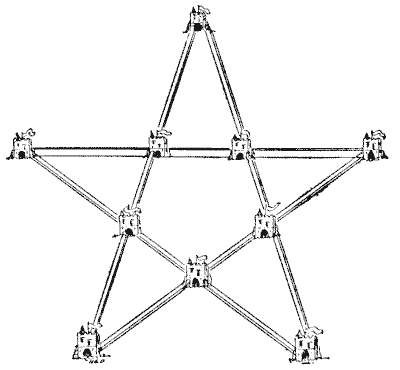 Sources:
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 206
-
CHERRIES AND PLUMS
 The illustration is a plan of a cottage as it stands surrounded by an orchard of fifty-five trees. Ten of these trees are cherries, ten are plums, and the remainder apples. The cherries are so planted as to form five straight lines, with four cherry trees in every line. The plum trees are also planted so as to form five straight lines with four plum trees in every line. The puzzle is to show which are the ten cherry trees and which are the ten plums. In order that the cherries and plums should have the most favourable aspect, as few as possible (under the conditions) are planted on the north and east sides of the orchard. Of course in picking out a group of ten trees (cherry or plum, as the case may be) you ignore all intervening trees. That is to say, four trees may be in a straight line irrespective of other trees (or the house) being in between. After the last puzzle this will be quite easy.
Sources:
The illustration is a plan of a cottage as it stands surrounded by an orchard of fifty-five trees. Ten of these trees are cherries, ten are plums, and the remainder apples. The cherries are so planted as to form five straight lines, with four cherry trees in every line. The plum trees are also planted so as to form five straight lines with four plum trees in every line. The puzzle is to show which are the ten cherry trees and which are the ten plums. In order that the cherries and plums should have the most favourable aspect, as few as possible (under the conditions) are planted on the north and east sides of the orchard. Of course in picking out a group of ten trees (cherry or plum, as the case may be) you ignore all intervening trees. That is to say, four trees may be in a straight line irrespective of other trees (or the house) being in between. After the last puzzle this will be quite easy.
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 207
-
THE TWENTY-ONE TREES
A gentleman wished to plant twenty-one trees in his park so that they should form twelve straight rows with five trees in every row. Could you have supplied him with a pretty symmetrical arrangement that would satisfy these conditions? Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 209
-
THE TWELVE MINCE-PIES
It will be seen in our illustration how twelve mince-pies may be placed on the table so as to form six straight rows with four pies in every row. The puzzle is to remove only four of them to new positions so that there shall be seven straight rows with four in every row. Which four would you remove, and where would you replace them?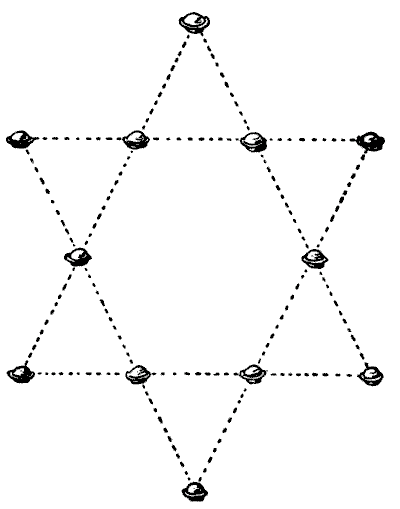 Sources:
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 211
-
TURKS AND RUSSI
This puzzle is on the lines of the Afridi problem published by me in Tit-Bits some years ago.
On an open level tract of country a party of Russian infantry, no two of whom were stationed at the same spot, were suddenly surprised by thirty-two Turks, who opened fire on the Russians from all directions. Each of the Turks simultaneously fired a bullet, and each bullet passed immediately over the heads of three Russian soldiers. As each of these bullets when fired killed a different man, the puzzle is to discover what is the smallest possible number of soldiers of which the Russian party could have consisted and what were the casualties on each side.
Sources:Topics:Combinatorics -> Combinatorial Geometry- Amusements in Mathematics, Henry Ernest Dudeney Question 213
-
THE NINE ALMONDS
"Here is a little puzzle," said a Parson, "that I have found peculiarly fascinating. It is so simple, and yet it keeps you interested indefinitely."
The reverend gentleman took a sheet of paper and divided it off into twenty-five squares, like a square portion of a chessboard. Then he placed nine almonds on the central squares, as shown in the illustration, where we have represented numbered counters for convenience in giving the solution.
"Now, the puzzle is," continued the Parson, "to remove eight of the almonds and leave the ninth in the central square. You make the removals by jumping one almond over another to the vacant square beyond and taking off the one jumped over—just as in draughts, only here you can jump in any direction, and not diagonally only. The point is to do the thing in the fewest possible moves."
The following specimen attempt will make everything clear. Jump `4` over `1, 5` over `9, 3` over `6, 5` over `3, 7` over `5` and `2, 4` over `7, 8` over `4`. But `8` is not left in the central square, as it should be. Remember to remove those you jump over. Any number of jumps in succession with the same almond count as one move.
Sources: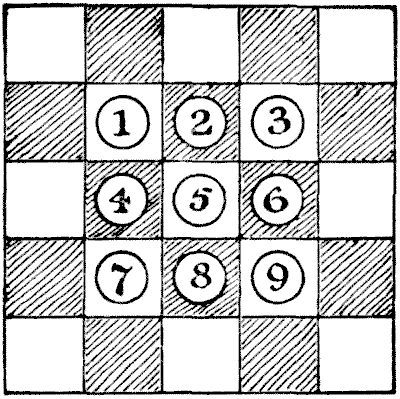
- Amusements in Mathematics, Henry Ernest Dudeney Question 229
-
THE FLY ON THE OCTAHEDRON
"Look here," said the professor to his colleague, "I have been watching that fly on the octahedron, and it confines its walks entirely to the edges. What can be its reason for avoiding the sides?"
"Perhaps it is trying to solve some route problem," suggested the other. "Supposing it to start from the top point, how many different routes are there by which it may walk over all the edges, without ever going twice along the same edge in any route?"
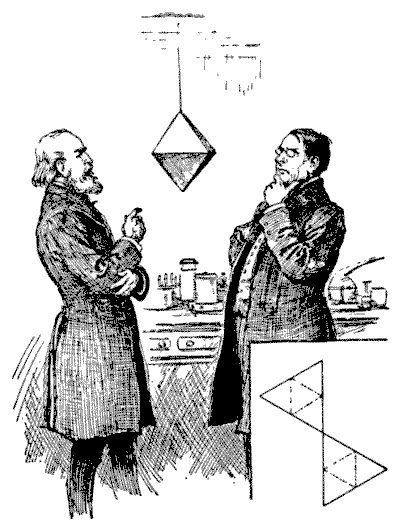
The problem was a harder one than they expected, and after working at it during leisure moments for several days their results did not agree—in fact, they were both wrong. If the reader is surprised at their failure, let him attempt the little puzzle himself. I will just explain that the octahedron is one of the five regular, or Platonic, bodies, and is contained under eight equal and equilateral triangles. If you cut out the two pieces of cardboard of the shape shown in the margin of the illustration, cut half through along the dotted lines and then bend them and put them together, you will have a perfect octahedron. In any route over all the edges it will be found that the fly must end at the point of departure at the top.
Sources:Topics:Combinatorics -> Combinatorial Geometry Combinatorics -> Graph Theory Geometry -> Solid Geometry / Geometry in Space -> Polyhedra -> Regular Polyhedra- Amusements in Mathematics, Henry Ernest Dudeney Question 245