Algebra, Word Problems
Word problems present mathematical challenges in a narrative or real-world context. Solving them requires translating the text into mathematical equations or expressions and then applying appropriate mathematical techniques. These can span arithmetic, algebra, geometry, etc.
Motion Problems Solving Word Problems "From the End" / Working Backwards-
THE THREE VILLAGES
I set out the other day to ride in a motor-car from Acrefield to Butterford, but by mistake I took the road going via Cheesebury, which is nearer Acrefield than Butterford, and is twelve miles to the left of the direct road I should have travelled. After arriving at Butterford I found that I had gone thirty-five miles. What are the three distances between these villages, each being a whole number of miles? I may mention that the three roads are quite straight.Sources:Topics:Geometry -> Plane Geometry -> Triangles Algebra -> Word Problems Geometry -> Plane Geometry -> Pythagorean Theorem- Amusements in Mathematics, Henry Ernest Dudeney Question 69
-
THE BASKET OF POTATOES
A man had a basket containing fifty potatoes. He proposed to his son, as a little recreation, that he should place these potatoes on the ground in a straight line. The distance between the first and second potatoes was to be one yard, between the second and third three yards, between the third and fourth five yards, between the fourth and fifth seven yards, and so on—an increase of two yards for every successive potato laid down. Then the boy was to pick them up and put them in the basket one at a time, the basket being placed beside the first potato. How far would the boy have to travel to accomplish the feat of picking them all up? We will not consider the journey involved in placing the potatoes, so that he starts from the basket with them all laid out.Sources:Topics:Algebra -> Word Problems Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence- Amusements in Mathematics, Henry Ernest Dudeney Question 74
-
THE PASSENGER'S FARE
At first sight you would hardly think there was matter for dispute in the question involved in the following little incident, yet it took the two persons concerned some little time to come to an agreement. Mr. Smithers hired a motor-car to take him from Addleford to Clinkerville and back again for £`3`. At Bakenham, just midway, he picked up an acquaintance, Mr. Tompkins, and agreed to take him on to Clinkerville and bring him back to Bakenham on the return journey. How much should he have charged the passenger? That is the question. What was a reasonable fare for Mr. Tompkins?
Sources:Topics:Algebra -> Word Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 75
-
THE BARREL OF BEER
A man bought an odd lot of wine in barrels and one barrel containing beer. These are shown in the illustration, marked with the number of gallons that each barrel contained. He sold a quantity of the wine to one man and twice the quantity to another, but kept the beer to himself. The puzzle is to point out which barrel contains beer. Can you say which one it is? Of course, the man sold the barrels just as he bought them, without manipulating in any way the contents.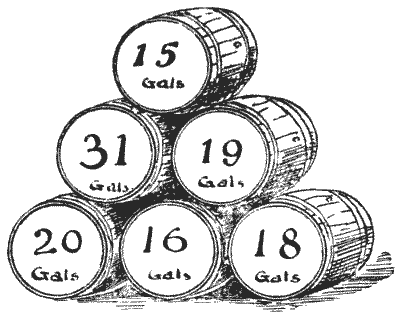 Sources:Topics:Arithmetic Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 3 and 9 Algebra -> Word Problems Logic -> Reasoning / Logic
Sources:Topics:Arithmetic Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 3 and 9 Algebra -> Word Problems Logic -> Reasoning / Logic- Amusements in Mathematics, Henry Ernest Dudeney Question 76
-
ADDING THE DIGITS
If I write the sum of money, £`987, 5`s. `4`½d.., and add up the digits, they sum to `36`. No digit has thus been used a second time in the amount or addition. This is the largest amount possible under the conditions. Now find the smallest possible amount, pounds, shillings, pence, and farthings being all represented. You need not use more of the nine digits than you choose, but no digit may be repeated throughout. The nought is not allowed. Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 89
-
THE SPOT ON THE TABLE
A boy, recently home from school, wished to give his father an exhibition of his precocity. He pushed a large circular table into the corner of the room, as shown in the illustration, so that it touched both walls, and he then pointed to a spot of ink on the extreme edge.

"Here is a little puzzle for you, pater," said the youth. "That spot is exactly eight inches from one wall and nine inches from the other. Can you tell me the diameter of the table without measuring it?"
The boy was overheard to tell a friend, "It fairly beat the guv'nor;" but his father is known to have remarked to a City acquaintance that he solved the thing in his head in a minute. I often wonder which spoke the truth.
Sources:Topics:Geometry -> Plane Geometry -> Circles Algebra -> Equations Algebra -> Word Problems Geometry -> Plane Geometry -> Pythagorean Theorem- Amusements in Mathematics, Henry Ernest Dudeney Question 97
-
ACADEMIC COURTESIES
In a certain mixed school, where a special feature was made of the inculcation of good manners, they had a curious rule on assembling every morning. There were twice as many girls as boys. Every girl made a bow to every other girl, to every boy, and to the teacher. Every boy made a bow to every other boy, to every girl, and to the teacher. In all there were nine hundred bows made in that model academy every morning. Now, can you say exactly how many boys there were in the school? If you are not very careful, you are likely to get a good deal out in your calculation. Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 98
-
THE THIRTY-THREE PEARLS
"A man I know," said Teddy Nicholson at a certain family party, "possesses a string of thirty-three pearls. The middle pearl is the largest and best of all, and the others are so selected and arranged that, starting from one end, each successive pearl is worth £`100` more than the preceding one, right up to the big pearl. From the other end the pearls increase in value by £`150` up to the large pearl. The whole string is worth £`65,000`. What is the value of that large pearl?"
"Pearls and other articles of clothing," said Uncle Walter, when the price of the precious gem had been discovered, "remind me of Adam and Eve. Authorities, you may not know, differ as to the number of apples that were eaten by Adam and Eve. It is the opinion of some that Eve `8` (ate) and Adam `2` (too), a total of `10` only. But certain mathematicians have figured it out differently, and hold that Eve `8` and Adam a total of `16`. Yet the most recent investigators think the above figures entirely wrong, for if Eve `8` and Adam `82`, the total must be `90`."
"Well," said Harry, "it seems to me that if there were giants in those days, probably Eve `81` and Adam `82`, which would give a total of `163`."
"I am not at all satisfied," said Maud. "It seems to me that if Eve `81` and Adam `812`, they together consumed `893`."
"I am sure you are all wrong," insisted Mr. Wilson, "for I consider that Eve `814` Adam, and Adam `8124` Eve, so we get a total of `8,938`."
"But, look here," broke in Herbert. "If Eve `814` Adam and Adam `81242` oblige Eve, surely the total must have been `82,056`!"
At this point Uncle Walter suggested that they might let the matter rest. He declared it to be clearly what mathematicians call an indeterminate problem.
Sources:Topics:Arithmetic Algebra -> Equations Algebra -> Word Problems Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence- Amusements in Mathematics, Henry Ernest Dudeney Question 99
-
THE LABOURER'S PUZZLE
Professor Rackbrane, during one of his rambles, chanced to come upon a man digging a deep hole.
"Good morning," he said. "How deep is that hole?"
"Guess," replied the labourer. "My height is exactly five feet ten inches."
"How much deeper are you going?" said the professor.
"I am going twice as deep," was the answer, "and then my head will be twice as far below ground as it is now above ground."
Rackbrane now asks if you could tell how deep that hole would be when finished.
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 100
-
THE TRUSSES OF HAY
Farmer Tompkins had five trusses of hay, which he told his man Hodge to weigh before delivering them to a customer. The stupid fellow weighed them two at a time in all possible ways, and informed his master that the weights in pounds were `110, 112, 113, 114, 115, 116, 117, 118, 120`, and `121`. Now, how was Farmer Tompkins to find out from these figures how much every one of the five trusses weighed singly? The reader may at first think that he ought to be told "which pair is which pair," or something of that sort, but it is quite unnecessary. Can you give the five correct weights? Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 101