בעיות מינימום ומקסימום

בעיות אלו, הידועות גם כבעיות אופטימיזציה, כוללות מציאת הערך הקטן ביותר (מינימום) או הגדול ביותר (מקסימום) של כמות או פונקציה תחת אילוצים נתונים. טכניקות יכולות לנוע מאי-שוויונים אלגבריים, חשיבה גאומטרית, ועד לחשבון דיפרנציאלי (אם רלוונטי).

  • גְּנֵבַת אוֹצַר הַטִּירָה

    הַדֶּרֶךְ הַמְּתוּחְכֶּמֶת בָּהּ נִגְנְבָה תֵּבַת אוֹצָר, הַמְּכִילָה בְּעִיקָרָהּ תַּכְשִׁיטִים וַאֲבָנִים יְקָרוֹת, מִטִּירַת גְּלוּמְהֶרְסְט, עָבְרָה כְּמָסֹרֶת בְּמִשְׁפַּחַת דֶּה גּוּרְנֵי. הַגַּנָּבִים הִתְכַּלְּלוּ מֵאִישׁ, נַעַר וְיֶלֶד קָטָן, שֶׁדֶּרֶךְ הַמִּלּוּט הַיְּחִידָה שֶׁלָּהֶם עִם תֵּבַת הָאוֹצָר הָיְתָה דֶּרֶךְ חַלּוֹן גָּבוֹהַּ. מִחוּץ לַחַלּוֹן הוּצַּב גַּלְגֶּלֶת, שֶׁעָלֶיהָ עָבַר חֶבֶל עִם סַל בְּכָל קָצֶה. כְּשֶׁסַּל אֶחָד הָיָה עַל הַקַּרְקַע, הַשֵּׁנִי הָיָה בַּחַלּוֹן. הַחֶבֶל סֻדַּר כָּךְ שֶׁהָאֲנָשִׁים בַּסַּל לֹא יָכְלוּ לַעֲזֹר לְעַצְמָם בְּאֶמְצָעוּתוֹ וְלֹא לְקַבֵּל עֶזְרָה מֵאֲחֵרִים. בְּקִצּוּר, הַדֶּרֶךְ הַיְּחִידָה לְשִׁמּוּשׁ בַּסַּלִּים הָיְתָה עַל יְדֵי הַצָּבַת מִשְׁקָל כָּבֵד יוֹתֵר בְּאֶחָד מֵהַשֵּׁנִי.

    עַכְשָׁו, מִשְׁקַל הָאִישׁ הָיָה `195` לִיבְּרוֹת, הַנַּעַר `105` לִיבְּרוֹת, הַיֶּלֶד `90` לִיבְּרוֹת וְתֵּבַת הָאוֹצָר `75` לִיבְּרוֹת. הַמִּשְׁקָל בַּסַּל הַיּוֹרֵד לֹא יָכֹל לַחְרֹג מִזֶּה שֶׁבַּשֵּׁנִי בְּיוֹתֵר מִ `15` לִיבְּרוֹת בְּלִי לִגְרֹם לִירִידָה כֹּה מְהִירָה שֶׁתִּהְיֶה מְסֻכֶּנֶת בְּיוֹתֵר לְבֶן אָדָם, אַף עַל פִּי שֶׁלֹּא תִּגְרֹם נֶזֶק לָרְכוּשׁ הַגָּנוּב. רַק שְׁנֵי אֲנָשִׁים, אוֹ אָדָם אֶחָד וְהָאוֹצָר, יָכְלוּ לְהָנִיחַ בְּאוֹתוֹ סַל בְּבַת אַחַת. אֵיךְ הֵם הִצְלִיחוּ לִבְרֹחַ וְלָקַחַת אִתָּם אֶת תֵּבַת הָאוֹצָר?

    הַחִידָה הִיא לִמְצֹא אֶת הַדֶּרֶךְ הַקְּצָרָה בְּיוֹתֵר לְבִצּוּעַ הַמַּעֲשֶׂה, שֶׁכְּשֶׁעַצְמוֹ אֵינוֹ קָשֶׁה. זִכְרוּ, אָדָם לֹא יָכוֹל לַעֲזֹר לְעַצְמוֹ עַל יְדֵי תְּלִיָּה עַל הַחֶבֶל, הַדֶּרֶךְ הַיְּחִידָה הִיא לָרֶדֶת "עִם מַהֲלוּמָה," כְּשֶׁהַמִּשְׁקָל בַּסַּל הַשֵּׁנִי כְּמִשְׁקָל נֶגְדִּי.

    מקורות:

  • שחקני הכדורגל

    "זהו משחק נפלא!" נשמע חובב נלהב קורא. "בסיום העונה שעברה, מבין שחקני הכדורגל שאני מכיר, לארבעה נשברה זרוע שמאל, לחמישה נשברה זרוע ימין, לשניים זרוע ימין הייתה בריאה, ולשלושה זרוע שמאל הייתה בריאה." האם תוכלו לגלות מההצהרה הזו מהו המספר הקטן ביותר של שחקנים שהדובר יכול היה להכיר?

    כלל לא נובע מכך שהיו ארבעה עשר אנשים, מכיוון שלדוגמה, שניים מהאנשים ששברו את זרוע שמאל יכולים להיות גם שניים מאלה שהייתה להם זרוע ימין בריאה.

    מקורות:

  • חידת שרשרת

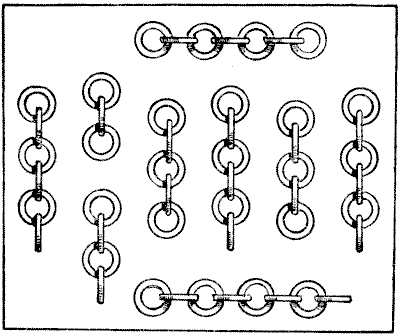    זוהי חידה המבוססת על רעיון נחמד שבו עסק לראשונה מר סם לויד המנוח. לאיש היו תשעה חלקי שרשרת, כפי שמוצג באיור. הוא רצה לחבר את חמישים החוליות האלה לשרשרת אינסופית אחת. יעלה פרוטה לפתוח כל חוליה ושתי פרוטות לרתך חוליה בחזרה, אבל הוא יכול לקנות שרשרת אינסופית חדשה באותו אופי ואיכות עבור `2`s. `2`d. מה היה המהלך הזול ביותר עבורו? אלא אם כן הקורא ערמומי הוא עלול למצוא את עצמו רחוק מהתשובה. מקורות:

  • הנחת מטבעות חצי פני

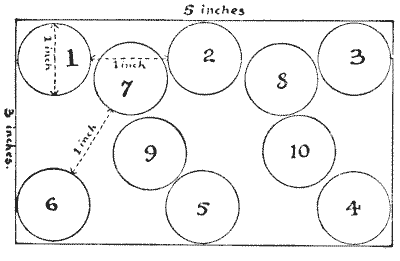    הנה חידה קטנה ומעניינת שהוצעה לי על ידי מר וו. טי. וויט. סמנו על דף נייר שטח מלבני של `5` אינץ' על `3` אינץ', ואז מצאו את המספר הגדול ביותר של מטבעות חצי פני שניתן להניח בתוך המתחם בתנאים הבאים. קוטר של מטבע חצי פני הוא בדיוק אינץ' אחד. הניחו את מטבע חצי הפני הראשון שלכם היכן שתרצו, ואז הניחו את המטבע השני בדיוק במרחק של אינץ' אחד מהראשון, את השלישי במרחק של אינץ' אחד מהשני, וכן הלאה. אסור לאף מטבע חצי פני לגעת במטבע אחר או לחצות את הגבול. האיור שלנו יבהיר את העניין בצורה מושלמת. מטבע מספר `2` נמצא במרחק אינץ' אחד ממספר `1`; מספר `3` במרחק אינץ' אחד ממספר `2`; מספר `4` במרחק אינץ' אחד ממספר `3`; אבל אחרי שמניחים את מספר `10`, איננו יכולים להתקדם בניסיון זה. עם זאת, אפשר היה להכניס עוד כמה מטבעות חצי פני. כמה יכול הקורא להניח? מקורות: