בעיות מינימום ומקסימום

בעיות אלו, הידועות גם כבעיות אופטימיזציה, כוללות מציאת הערך הקטן ביותר (מינימום) או הגדול ביותר (מקסימום) של כמות או פונקציה תחת אילוצים נתונים. טכניקות יכולות לנוע מאי-שוויונים אלגבריים, חשיבה גאומטרית, ועד לחשבון דיפרנציאלי (אם רלוונטי).

• נשות השוק

  מספר נשות שוק מכרו את מוצריהן השונים במחיר מסוים לליברה (שונה בכל מקרה), וכל אחת קיבלה את אותו הסכום - `2`s. `2`½d. מהו המספר הגדול ביותר של נשים שיכלו להיות שם? המחיר לליברה בכל מקרה חייב להיות כזה שניתן לשלם אותו בכסף מקובל.
  נושאים:

  אריתמטיקה אלגברה -> בעיות מילוליות תורת המספרים -> המחלק המשותף המקסימלי והכפולה המשותפת המינימלית בעיות מינימום ומקסימום
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 18

• תַּעֲלוּמַת קְנִיּוֹת

  שתי נשים נכנסו לחנות שבה, מתוך מוזרות משונה, לא ניתן עודף, וביצעו רכישות בסכום כולל של פחות מחמישה שילינג. "את יודעת," אמרה אחת הנשים, "אני מגלה שאצטרך לא פחות משישה מטבעות מקובלים של הממלכה כדי לשלם עבור מה שקניתי." האישה השנייה התבוננה לרגע, ואז קראה: "בצירוף מקרים מוזר, אני בדיוק באותה דילמה." "אז נשלם את שני החשבונות יחד." אבל, לתדהמתן, הן עדיין נזקקו לשישה מטבעות. מהו הסכום הקטן ביותר האפשרי של הקניות שלהן - שניהם שונים?
  נושאים:

  אריתמטיקה אלגברה -> בעיות מילוליות בעיות מינימום ומקסימום
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 24

• השמיכה של גברת פרקינס

  ניתן לראות שבמקרה זה שמיכת הטלאים המרובעת בנויה מ-`169` חלקים. החידה היא למצוא את המספר הקטן ביותר האפשרי של חלקים מרובעים שמהם יכולה להיות מורכבת השמיכה ולהראות כיצד ניתן לחבר אותם יחד. או, כדי להציג זאת הפוך, חלקו את השמיכה למספר הקטן ביותר האפשרי של חלקים מרובעים רק על ידי חיתוך התפרים.
  נושאים:

  גאומטריה -> גאומטריה במישור בעיות מינימום ומקסימום קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 173

• חידת חולבת הפרות

  הנה חידה כפרית קטנה, אשר במבט ראשון עשויה להוביל את הקורא להניח שהיא מעמיקה מאוד, וכוללת חישובים מורכבים. הוא אף עשוי לטעון שאי אפשר לתת תשובה כלשהי אלא אם כן נאמר לנו משהו מוגדר לגבי המרחקים. ובכל זאת היא ממש "ילדותית ותמימה."

   

  בפינת שדה נראית חולבת חולבת פרה, ובצד השני של השדה נמצאת המחלבה, לשם יש להעביר את החלב. אבל שמו לב שהאישה הצעירה תמיד יורדת לנהר עם הדלי שלה לפני שהיא חוזרת למחלבה. כאן הקורא החשדן אולי ישאל מדוע היא מבקרת בנהר. אני יכול רק לענות שזה לא ענייננו. החלב לכאורה מיועד כולו לצריכה מקומית.

  "לאן את הולכת, עלמה יפה שלי?"
  "לנהר, אדוני," היא אמרה.
  "אני לא אבחר את המחלבה שלך, עלמה יפה שלי."
  "אף אחד לא שאל אותך, אדוני," היא אמרה.

  
  

  אם למישהו הייתה סקרנות בעניין, רוח עצמאית כזו תנטרל אותו לחלוטין. אז נעבור מנקודת המבט של מוסר מסחרי לנושא החידה.

  מתחו קו משרפרף החליבה אל הנהר ומשם אל דלת המחלבה, אשר יציין את המסלול הקצר ביותר האפשרי עבור החולבת. זה הכל. קל מאוד לציין את הנקודה המדויקת על גדת הנהר שאליה עליה לכוון את צעדיה אם היא רוצה את ההליכה הקצרה ביותר האפשרית. האם אתה יכול למצוא את הנקודה הזו?

  נושאים:

  בעיות מינימום ומקסימום גאומטריה -> גאומטריה במישור -> העתקות של מישור -> העתקות חפיפה (איזומטריות) -> שיקוף
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 187

• קיר החידה

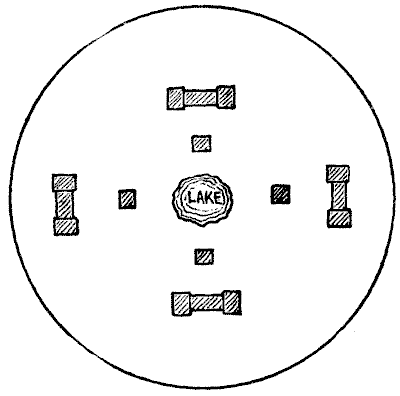  היה אגם קטן, סביבו בנו ארבעה אנשים עניים את בקתותיהם. ארבעה אנשים עשירים בנו לאחר מכן את אחוזותיהם, כפי שמוצג באיור, והם רצו שהאגם יהיה רק לרשותם, ולכן הורו לבנאי להקים את החומה הקצרה ביותר האפשרית שתמנע מהבעלים של הבקתות גישה לאגם, אך תעניק להם גישה חופשית לאגם. איך היה צריך לבנות את החומה?
  נושאים:

  גאומטריה בעיות מינימום ומקסימום
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 192

• איך ליצור בורות מים

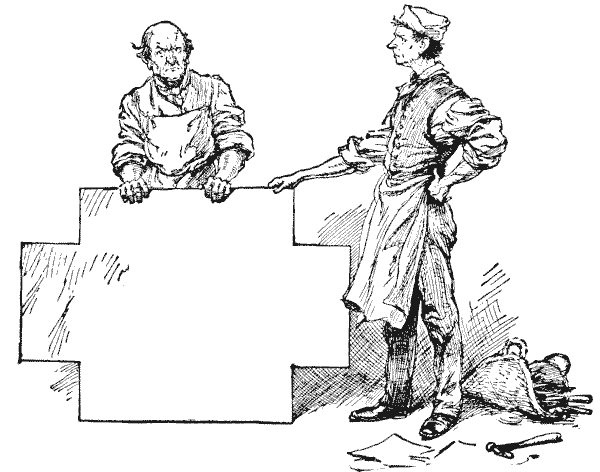  לידידנו באיור יש יריעת אבץ גדולה, שממדיה (לפני החיתוך) שמונה רגל על שלוש רגל, והוא חתך פיסות מרובעות (כולן באותו גודל) מארבע הפינות וכעת הוא מציע לקפל את הצדדים, להלחים את הקצוות, ולהכין בור מים. אבל הנקודה שמבלבלת אותו היא זו: האם הוא חתך את פיסות הריבוע בגודל הנכון, כך שהבור יכיל את הכמות הגדולה ביותר האפשרית של מים? אתם רואים, אם חותכים אותם קטנים מאוד, מקבלים בור רדוד מאוד; אם חותכים אותם גדולים, מקבלים בור גבוה וצר. הכל עניין של למצוא דרך לחתוך את ארבע פיסות הריבוע האלה בדיוק בגודל הנכון. איך נוכל להימנע מלחתוך אותם קטנים מדי או גדולים מדי?
  נושאים:

  אלגברה -> בעיות מילוליות בעיות מינימום ומקסימום
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 201

• חידת החרוט

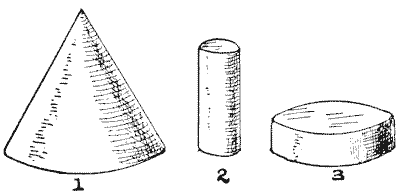  יש לי חרוט עץ, כפי שמוצג באיור `1`. איך עליי לחתוך ממנו את הגליל הגדול ביותר האפשרי? ניתן לראות שאני יכול לחתוך אחד שהוא ארוך ודק, כמו באיור `2`, או קצר ועבה, כמו באיור `3`. אבל אף אחד מהם אינו הגדול ביותר האפשרי. ילד יכול לומר לכם היכן לחתוך, אם הוא היה מכיר את הכלל. האם תוכלו למצוא את הכלל הפשוט הזה?
  נושאים:

  גאומטריה -> גאומטריה במרחב בעיות מינימום ומקסימום
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 202

• רצים - לא מוגנים

  הנח מספר מינימלי ככל האפשר של רצים על לוח שחמט רגיל, כך שכל משבצת בלוח תהיה מאוישת או מותקפת. ניתן לראות שלצריח יש טווח גדול יותר מלרץ: משום שבכל מקום שתציב את הראשון, הוא תמיד יתקוף ארבע עשרה משבצות אחרות; ואילו האחרון יתקוף שבע, תשע, אחת עשרה או שלוש עשרה משבצות, בהתאם למיקום האלכסון עליו הוא מונח. וכדאי כאן לציין שכאשר אנו מדברים על "אלכסונים" בהקשר ללוח השחמט, איננו מגבילים את עצמנו לשני האלכסונים הארוכים מפינה לפינה, אלא כוללים את כל הקווים הקצרים יותר המקבילים לקווים אלה. כדי למנוע אי הבנות בהמשך, כדאי שהקורא ישים לב לעובדה זו בקפידה.
  נושאים:

  בעיות מינימום ומקסימום קומבינטוריקה -> צביעות -> צביעת שחמט
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 297

• רצים - שמורים

  כמה רצים נחוצים כדי שכל משבצת תהיה מאויישת או מותקפת, וכל רץ יהיה שמור על ידי רץ אחר? ואיך ניתן למקם אותם?
  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית בעיות מינימום ומקסימום קומבינטוריקה -> צביעות -> צביעת שחמט
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 298

• פאזל אריזה

  כפי שכולנו יודעים מניסיון, לעתים קרובות נדרשת תושייה רבה באריזת חפצים לקופסה, אם לא רוצים לבזבז מקום שלא לצורך. אדם סיפר לי פעם שהיו לו מספר רב של כדורי ברזל, שקוטרם בדיוק שני אינץ' כל אחד, והוא רצה לארוז כמה שיותר מהם לתוך קופסה מלבנית באורך `24` `9/10` אינץ', ברוחב `22` `4/5` אינץ' ובעומק `14` אינץ'. מהו המספר הגדול ביותר של כדורים שהוא יכול לארוז בקופסה הזו?
  נושאים:

  גאומטריה -> גאומטריה במרחב אריתמטיקה בעיות מינימום ומקסימום
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 370