Geometry

Geometry is the branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogues. Expected questions involve calculating lengths, angles, areas, and volumes of various shapes, understanding geometric theorems, and solving problems related to spatial reasoning.

• Question

  Find the area marked by the question mark:

  

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation

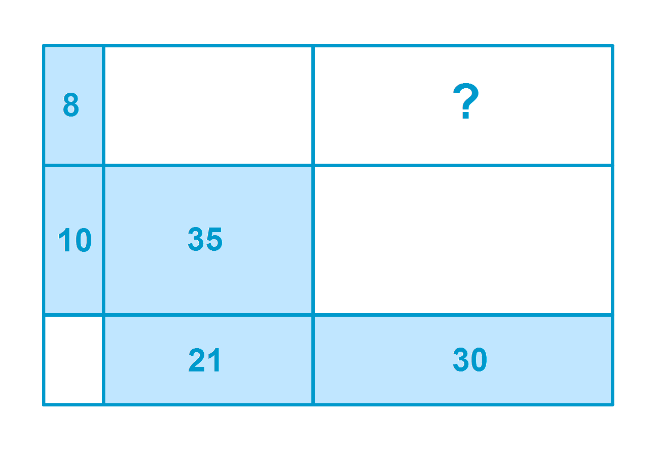
• Question

  Consider an arbitrary triangle. Draw tangents to the inscribed circle parallel to the sides of the triangle. These tangents cut off three smaller triangles from the original triangle. Prove that the sum of the radii of the inscribed circles of these smaller triangles is equal to the radius of the inscribed circle of the original triangle.

  Topics:

  Geometry -> Plane Geometry -> Circles -> Tangent to a Circle Geometry -> Plane Geometry -> Triangles -> Triangle Similarity

• Question

  `101` points are located on a circle. Which polygons with vertices at these points are more numerous – polygons with `51` sides or polygons with `50` sides?

  Topics:

  Combinatorics -> Binomial Coefficients and Pascal's Triangle Combinatorics -> Matchings Geometry -> Plane Geometry -> Circles

• Question

  A square is divided into several convex polygons (more than `1`), each of which has a different number of sides. Prove that among these polygons there is a triangle.

  Topics:

  Combinatorics -> Pigeonhole Principle Combinatorics -> Combinatorial Geometry Combinatorics -> Graph Theory Geometry -> Plane Geometry -> Triangles Proof and Example -> Proof by Contradiction Geometry -> Solid Geometry / Geometry in Space -> Polyhedra Minimum and Maximum Problems / Optimization Problems

• Question

  Is it possible to cut a triangle into four convex shapes: a triangle, a quadrilateral, a pentagon, and a hexagon?

  Topics:

  Geometry -> Plane Geometry -> Triangles Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Consider an arbitrary hexagon and denote the midpoints of its sides by `M_1,M_2,M_3,M_4,M_5,M_6`. Prove that the segments `M_1M_2`, `M_3M_4` and `M_5M_6` can form a triangle, even without rotating these segments.

  Topics:

  Geometry -> Vectors

• Question

  Given two parallelograms: `ABCD` and `A^'B^'C^'D^'`. Let `A^″ ` be the midpoint of the segment `A\A^'`, `B^″ ` be the midpoint of the segment `B\B^'`, and so on. Prove that `A^″B^″ C^″ D^″ ` is a parallelogram.

  Topics:

  Geometry -> Plane Geometry Geometry -> Vectors

• Question

  How many triangles are there in the image?

  

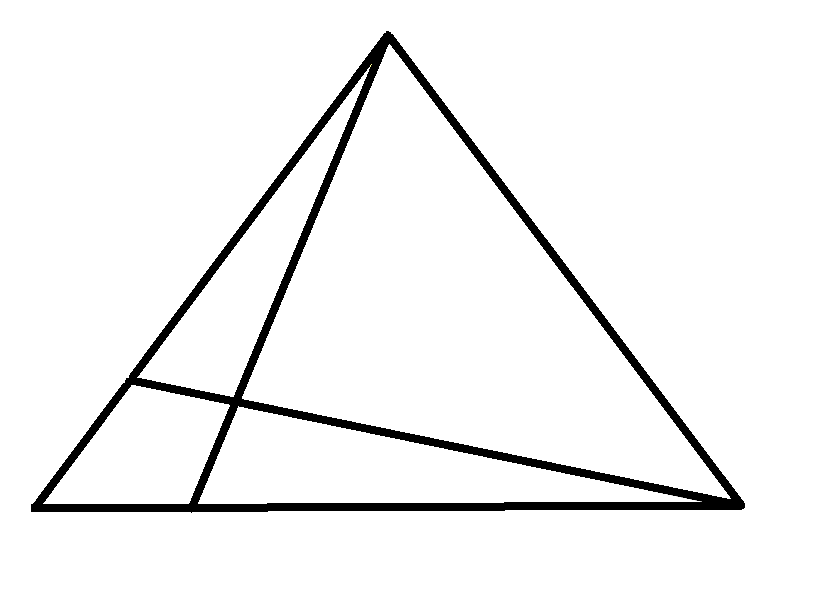  Topics:

  Geometry -> Plane Geometry -> Triangles Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures

• Question

  In the figure, a semicircle is shown with three circles inscribed within it: the large circle, tangent to the diameter of the semicircle at its center, and two smaller circles on the sides, symmetrically arranged. Which area is larger: the shaded area or the unshaded area?

  

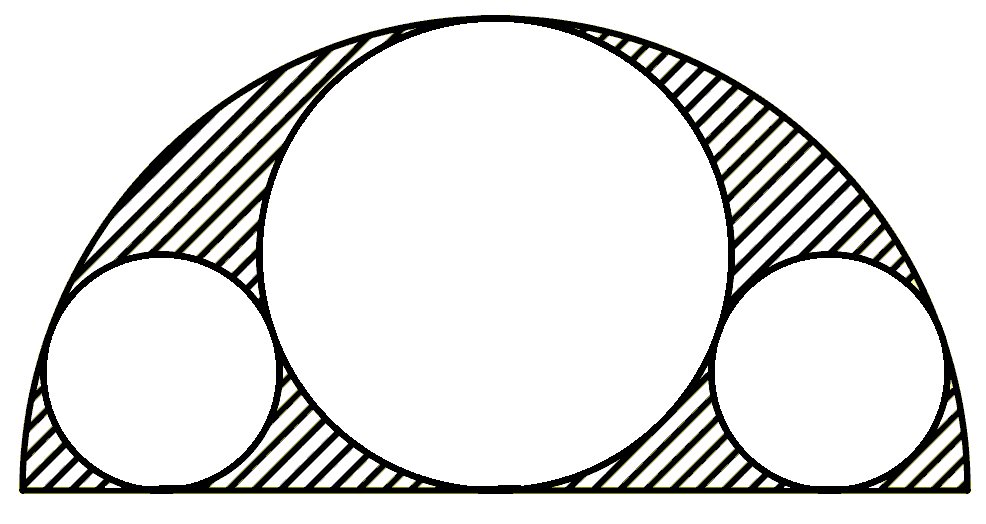  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Symmetry

• Quarter Yin-Yang

  The shape in the drawing is constructed as follows: Divide the diameter of a semicircle into two equal parts, and construct two additional semicircles on them as diameters: one inwards, and one outwards.

  

  Divide the shape into two congruent parts.

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems