Geometry

Geometry is the branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogues. Expected questions involve calculating lengths, angles, areas, and volumes of various shapes, understanding geometric theorems, and solving problems related to spatial reasoning.

Solid Geometry / Geometry in Space Trigonometry Spherical Geometry Plane Geometry Vectors

• Perpendicular Hands

  How many times a day do the hour and minute hands lie on the same line, forming an angle of `180^@`? Are any of these lines perpendicular to each other?

  Topics:

  Logic Proof and Example -> Proof by Contradiction Geometry -> Plane Geometry -> Angle Calculation

• Question

  In the plane, a square and a point `P` are given. Prove that it is impossible for the distances from `P` to the vertices of the square to be `1`, `1`, `2`, and `3` centimeters?

  Topics:

  Geometry -> Plane Geometry -> Triangles Proof and Example -> Proof by Contradiction Geometry -> Plane Geometry -> Triangle Inequality

• Stack of Papers

  Several identical rectangular sheets of paper lie on a table. It is known that the top sheet covers more than half the area of every other sheet. Is it necessarily possible to stick a pin into the table that will go through all these sheets?

  Topics:

  Combinatorics -> Pigeonhole Principle Combinatorics -> Combinatorial Geometry Geometry -> Area Calculation Geometry -> Plane Geometry -> Symmetry

• Question

  Semicircles are constructed on the legs and hypotenuse of a right-angled triangle, as shown in the figure. Which area is larger—the hatched area or the shaded area?

  

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Pythagorean Theorem

• Question

  Prove that there is no polyhedron with `7` edges.

  Topics:

  Combinatorics -> Graph Theory Proof and Example -> Proof by Contradiction Geometry -> Solid Geometry / Geometry in Space -> Polyhedra

• Question

  A number of lines and circles are drawn in the plane. Prove that it is possible to color the regions into which the plane is divided using two colors such that neighboring regions (those sharing a line segment or arc) are colored with different colors.

  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Induction (Mathematical Induction) Geometry -> Plane Geometry Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Colorings

• Question

  Prove that every polyhedron has at least two faces with the same number of edges.

  Topics:

  Combinatorics -> Pigeonhole Principle Combinatorics -> Graph Theory Geometry -> Solid Geometry / Geometry in Space -> Polyhedra

• Question

  Cut the given shape into two congruent parts:

  

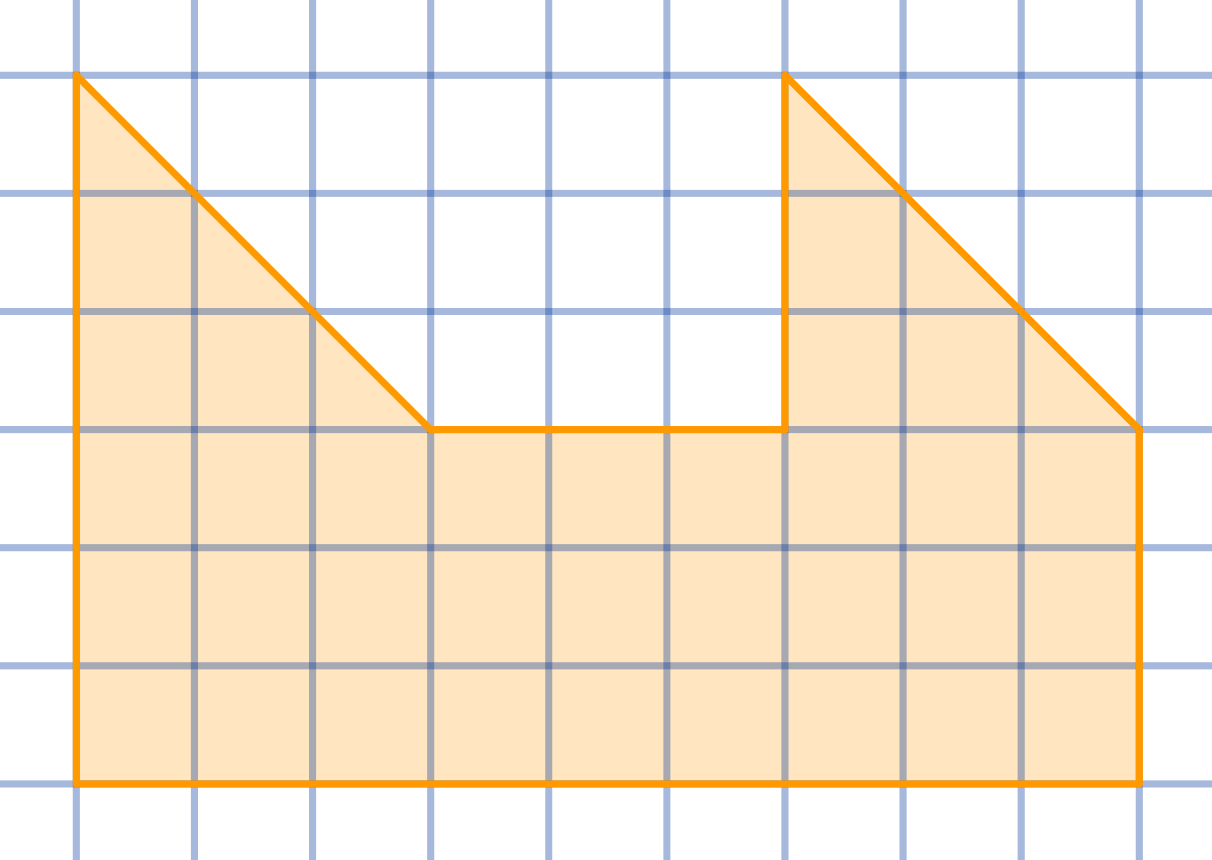  Topics:

  Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries)

• Question

  Cut the given shape into two congruent parts:

  

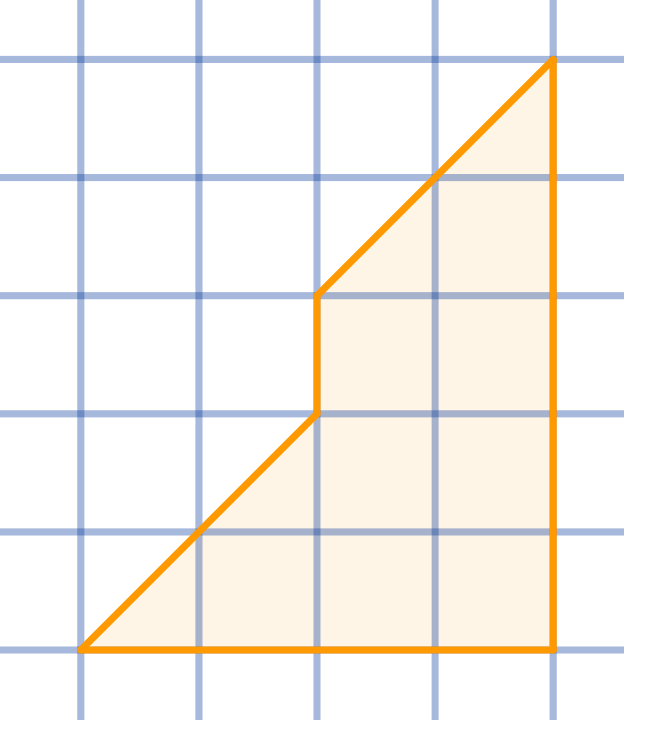  Topics:

  Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries)

• Question

  Cut the given shape into three congruent parts:

  

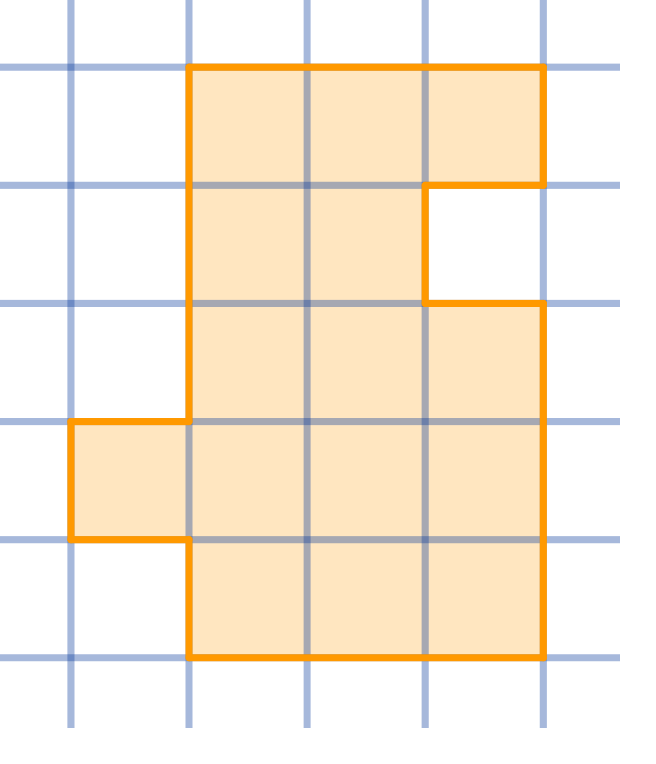  Topics:

  Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries)