几何学, 平面几何学, 三角形, 三角形全等
三角形全等涉及确定两个三角形是否具有完全相同的大小和形状。问题涉及应用全等公设(如SSS、SAS、ASA、AAS)来证明三角形全等,并推断对应边和角的相等性。
-
问题
将一个正方形切成三块,然后用它们组成一个各边都不相等的锐角三角形。
-
问题
两个全等的三角形形成一个如图像所示的六芒星。证明阴影区域的面积等于条纹区域的面积。
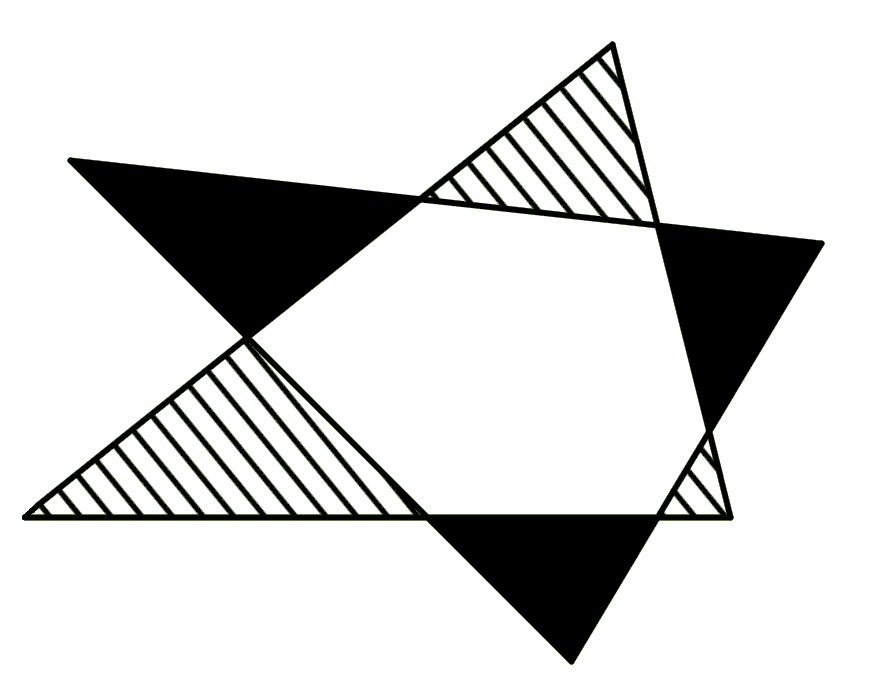
-
五边形
在凸五边形 `ABCDE` 中,已知: `AE=AD`, `AB=AC` 且 `angle CAD=angle ABE + angle AEB`。
在三角形 `ABE` 中,作中线 `AM`。 证明: `AM` 的长度是线段 `CD` 长度的一半。
来源: -
问题
给定一个具有 n 个顶点的正多边形。计算顶点与多边形顶点重合的不同三角形(非全等三角形)的数量
来源: -
点在哪里?
在凸六边形 ABCDEF 中,三角形
ACE 和 BDF 是等边且全等的。证明
连接六边形对边中点的三条线段
交于一点。来源: -
在线条上的三角形
六个全等的等腰三角形如图所示放置在一起。
证明点 C、F 和 M 在一条直线上。 来源:
来源: