שעשועונים במתמטיקה, הנרי ארנסט דודני

  • שאלה 231 - צלחות ומטבעות

    הנח שתים עשרה צלחות, כפי שמוצג, על שולחן עגול, עם מטבע או תפוז בכל צלחת. התחל מכל צלחת שתרצה, ותמיד בכיוון אחד סביב השולחן, קח מטבע אחד, העבר אותו מעל שני מטבעות אחרים והנח אותו בצלחת הבאה. המשך שוב; קח מטבע נוסף, ולאחר שהעברת אותו מעל שני מטבעות, הנח אותו בצלחת; וכך המשך במסעך. יש להסיר שישה מטבעות בלבד, וכאשר אלה הונחו, צריכים להיות שני מטבעות בכל אחת משש צלחות ושש צלחות ריקות. נקודה חשובה בחידה היא להקיף את השולחן כמה שפחות פעמים. לא משנה אם שני המטבעות שעליהם עוברים נמצאים בצלחת אחת או בשתי צלחות, וגם לא כמה צלחות ריקות מעבירים מטבע מעליהן. אבל אתה חייב תמיד ללכת בכיוון אחד סביב השולחן ולסיים בנקודה ממנה יצאת. היד שלך, כלומר, מתקדמת בהתמדה בכיוון אחד, מבלי לזוז אחורה.

  • שאלה 232 - לתפוס את העכברים

     

    "שחקו честно!" אמרו העכברים. "אתם מכירים את חוקי המשחק."

    "כן, אני מכיר את החוקים," אמר החתול. "אני צריך להסתובב במעגל, בכיוון שבו אתם מסתכלים, ולאכול כל עכבר שלושה-עשר, אבל אני חייב לשמור את העכבר הלבן לפינוק בסוף. שלושה עשר הוא מספר חסר מזל, אבל אעשה כמיטב יכולתי להיענות לבקשתכם."

    "תזדרז אם כן!" צעקו העכברים.

    "תנו לבחור זמן לחשוב," אמר החתול. "אני לא יודע באיזה מכם להתחיל. אני חייב להבין את זה.

    "בזמן שהחתול פתר את החידה הוא נרדם, וכך הכישוף נשבר, והעכברים חזרו הביתה בשלום. באיזה עכבר היה צריך החתול להתחיל לספור כדי שהעכבר הלבן יהיה האחרון שנאכל?

    כאשר הקורא פתר את החידה הקטנה הזו, הנה חידה שנייה בשבילו. מהו המספר הקטן ביותר שהחתול יכול לספור סביב המעגל, אם הוא חייב להתחיל בעכבר הלבן (לקרוא לזה "אחד" בספירה) ועדיין לאכול את העכבר הלבן אחרון מכולם?

    וכחידה שלישית נסו לגלות מהו המספר הקטן ביותר שהחתול יכול לספור סביב אם הוא חייב להתחיל בעכבר הלבן (לקרוא לזה "אחד") ולהפוך את העכבר הלבן לשלישי שנאכל.

  • שאלה 233 - המוכר גבינות האקסצנטרי

    מוכר הגבינות המתואר באיור הוא חובב חידות מושבע. אחת החידות האהובות עליו היא ערימת גבינות במחסן שלו, שעשוע שהוא מוצא בו פעילות גופנית טובה כמו גם תרגול מחשבתי. הוא מניח שש עשרה גבינות על הרצפה בשורה ישרה ואז הופך אותן לארבע ערימות, עם ארבע גבינות בכל ערימה, על ידי העברת גבינה מעל ארבע אחרות. אם תשתמשו בשש עשרה אסימונים ותמספרו אותם בסדר מ-`1` עד `16`, תוכלו להניח את `1` על `6, 11` את `7` על `4`, וכן הלאה, עד שיהיו ארבעה בכל ערימה. ניתן לראות שזה לא משנה אם ארבעת אלה שמעבירים מעליהם עומדים לבד או בערימה; הם נספרים בדיוק אותו הדבר, ותמיד אפשר לשאת גבינה לכל כיוון. ישנן דרכים רבות ושונות לעשות זאת בשנים עשר מהלכים, כך שזה הופך למשחק טוב של "סבלנות" לנסות לפתור אותו כך שארבע הערימות יישארו במקומות מותנים שונים. לדוגמה, נסו להשאיר את הערימות בקצוות הקיצוניים של השורה, במספרים `1, 2, 15` ו-`16`; זה די קל. אחר כך נסו להשאיר שלוש ערימות יחד, במספרים `13, 14`, ו-`15`. שוב, שחקו כך שהן יישארו במספרים `3, 5, 12`, ו-`14`.

  • שאלה 234 - חידת ההחלפה

    הנה חידה קטנה ומשעשעת עם העברת חיילים. אתה צריך רק שנים עשר חיילים—שישה מצבע אחד, המסומנים A, C, E, G, I ו-K, והשישה האחרים מסומנים B, D, F, H, J ו-L. אתה מניח אותם תחילה על הדיאגרמה, כפי שמוצג באיור, והחידה היא להביא אותם לסדר אלפביתי רגיל, כדלקמן:—

    A B C D
    E F G H
    I J K L

    המהלכים מתבצעים על ידי החלפות של צבעים מנוגדים העומדים על אותו קו. כך, G ו-J יכולים להחליף מקומות, או F ו-A, אבל אינך יכול להחליף את G ו-C, או F ו-D, מכיוון שבמקרה אחד שניהם לבנים ובמקרה השני שניהם שחורים. האם אתה יכול להביא את הסידור הנדרש בשבע עשרה החלפות?

     

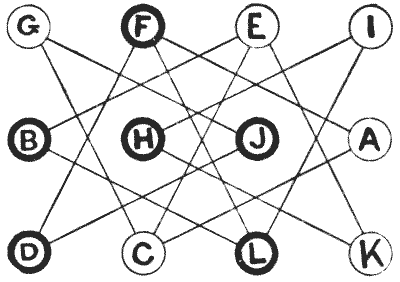
    אי אפשר לעשות זאת בפחות מהלכים. החידה באמת הרבה יותר קלה ממה שהיא נראית, אם תוקפים אותה כראוי.

  • שאלה 235 - אימון טורפדו

    אם צי של שישה עשר ספינות מלחמה עוגן ומוקף על ידי האויב, כמה ספינות עשויות לטבוע אם כל טורפדו, המשוגר בקו ישר, יעבור מתחת לשלוש ספינות ויטביע את הרביעית? בתרשים סידרנו את הצי במבנה ריבועי, שם ניתן לראות שאפשר להטביע עד שבע ספינות (אלו בשורה העליונה ובעמודה הראשונה) על ידי ירי הטורפדות המסומנים על ידי החצים. בעגינת הצי כרצוננו, עד כמה נוכל להגדיל את המספר הזה? זכרו שכל ספינה עוקבת טובעת לפני שיגור טורפדו נוסף, וכל טורפדו נע בכיוון אחר; אחרת, על ידי הצבת הספינות בקו ישר, אנו עשויים להטביע עד שלושה עשר! זהו מחקר קטן ומעניין בלוחמה ימית, ומעשי במיוחד - בתנאי שהאויב יאפשר לך לסדר את הצי שלו לנוחיותך ויבטיח לשכב בשקט ולא לעשות דבר!

  • שאלה 236 - חידת הכובעים

    עשרה כובעים נתלו על יתדות כפי שמוצג באיור—חמישה כובעי משי וחמישה כובעי לבד, "בולרים," לסירוגין משי ולבד. שתי היתדות בקצה השורה היו ריקות. 

     

    החידה היא להסיר שני כובעים סמוכים אל היתדות הפנויות, לאחר מכן שני כובעים סמוכים אחרים אל היתדות שאינן מאוכלסות כעת, וכן הלאה עד שחמישה זוגות הועברו והכובעים שוב תלויים בשורה רציפה, אך עם כל כובעי המשי יחד וכל כובעי הלבד יחד.

    זכרו, שני הכובעים המוסרים חייבים להיות תמיד סמוכים זה לזה, ועליכם לקחת אחד בכל יד ולהניח אותם על היתדות החדשות שלהם מבלי להפוך את מיקומם היחסי. אסור לכם לחצות את הידיים, וגם לא לתלות אחד בכל פעם.

    האם תוכלו לפתור את החידה הישנה הזו, שאני נותן כמבוא לזו הבאה? נסו זאת עם אסימונים משני צבעים או עם מטבעות, וזכרו ששתי היתדות הריקות חייבות להישאר בקצה אחד של השורה.

  • שאלה 237 - בנים ובנות

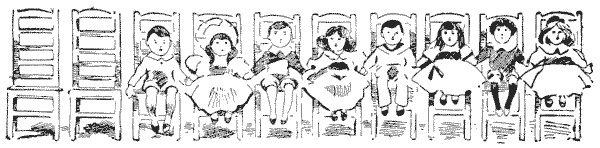
    אם תסמנו עשרה חלוקות על דף נייר כדי לייצג את הכיסאות, ותשתמשו בשמונה אסימונים ממוספרים עבור הילדים, יהיה לכם בילוי מרתק. תנו למספרים האי-זוגיים לייצג בנים ולמספרים הזוגיים בנות, או שתוכלו להשתמש באסימונים משני צבעים, או במטבעות.

    החידה היא להסיר שני ילדים היושבים בכיסאות סמוכים ולהניח אותם בשני כיסאות ריקים, כאשר הם מחליפים צדדים תחילה; לאחר מכן הסירו זוג ילדים שני מכיסאות סמוכים והניחו אותם בשני הכיסאות הפנויים כעת, כשהם מחליפים צדדים; וכן הלאה, עד שכל הבנים יהיו ביחד וכל הבנות ביחד, כאשר שני הכיסאות הריקים בקצה אחד כמו עכשיו. כדי לפתור את החידה, עליכם לעשות זאת בחמישה מהלכים. שני הילדים חייבים תמיד להילקח מכיסאות הצמודים זה לזה; וזכרו את הנקודה החשובה של החלפת הצדדים בין שני הילדים, שכן זהו המאפיין הייחודי של החידה. על ידי "החלפת צדדים" אני פשוט מתכוון שאם, לדוגמה, תזיזו תחילה את `1` ו-`2` לכיסאות הריקים, אז הכיסא הראשון (החיצוני) יאוכלס על ידי `2` והשני על ידי `1`. 

  • שאלה 238 - סידור קופסאות הריבה

    קרה שראיתי ילדה קטנה ממיינת ריבות בארון עבור אמה. היא הניחה כל סוג ריבה בנפרד על המדפים. שמתי לב שהיא לקחה צנצנת שזיפים ביד אחת וצנצנת דומדמניות ביד השנייה והחליפה ביניהן; אחר כך היא החליפה תות שדה עם פטל, וכן הלאה. היה מעניין לראות כמה טרחה מיותרת היא נתנה לעצמה על ידי ביצוע יותר החלפות ממה שהיה צורך, וחשבתי שזה יכול להפוך לחידה טובה.

     

    כפי שניתן לראות באיור, דורותי הקטנה צריכה לתפעל עשרים וארבע קופסאות ריבה גדולות במספר תאים תואם. היא רוצה לסדר אותן בסדר מספרי נכון—כלומר, `1, 2, 3, 4, 5, 6` על המדף העליון, `7, 8, 9, 10, 11, 12` על המדף הבא, וכן הלאה. עכשיו, אם היא תמיד לוקחת קופסה אחת ביד ימין ואחת ביד שמאל ומחליפה ביניהן, כמה מההחלפות האלה יהיו נחוצות כדי לסדר את כל קופסאות הריבה בסדר הנכון? באופן טבעי היא תחליף קודם את `1` ואת `3`, אחר כך את `2` ואת `3`, ואז יהיו לה שלוש הקופסאות הראשונות במקומן. איך היית מייעץ לה להמשיך מכאן? הניחו כמה אסימונים ממוספרים על דף נייר המחולק למשבצות עבור התאים, ותגלו שזו חידה משעשעת.

  • שאלה 239 - חידה לנוער

    במשך שנים התייעצו איתי חבריי הצעירים ללא הרף לגבי החידה הקטנה הזו. נראה שרוב הילדים מכירים אותה, ובכל זאת, באופן מוזר למדי, הם תמיד לא מכירים את התשובה. השאלה שהם תמיד שואלים היא, "בבקשה, תגיד לי אם זה באמת אפשרי." אני מאמין שהודיני הקוסם נהג לחבב מאוד לתת אותה לחבריו הילדים, אבל אני לא יכול לומר אם הוא המציא את החידה הקטנה או לא. אין ספק שמספר גדול של קוראיי ישמחו לקבל את פתרון המסתורין, אז אני לא מתנצל על הצגת ה"טיזר" הישן הזה.

    החידה היא לצייר בשלוש משיכות עיפרון את הדיאגרמה שהילדה הקטנה מציגה באיור. כמובן, אסור להרים את העיפרון מהנייר במהלך משיכה או לעבור על אותו קו פעם שנייה. תגלו שאתם יכולים להכניס חלק גדול מהדמות במשיכה רציפה אחת, אבל זה תמיד ייראה כאילו ארבע משיכות נחוצות. 

     

    צורה נוספת של החידה היא לצייר את הדיאגרמה על לוח ואז למחוק אותה בשלוש מחיקות.

  • שאלה 240 - דגל היוניון ג'ק

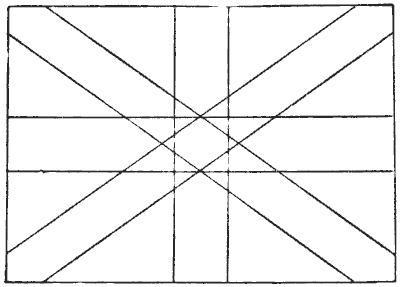    האיור הוא סקיצה גסה הדומה במידת מה לדגל הבריטי, היוניון ג'ק. לא ניתן לצייר את כולו מבלי להרים את העיפרון מהנייר או לעבור על אותו קו פעמיים. החידה היא לגלות בדיוק כמה מהציור אפשר לעשות מבלי להרים את העיפרון או לעבור פעמיים על אותו קו. קחו את העיפרון שלכם ובדקו מה הכי טוב שאתם יכולים לעשות.