שעשועונים במתמטיקה, הנרי ארנסט דודני

  • שאלה 421 - חידת שרשרת

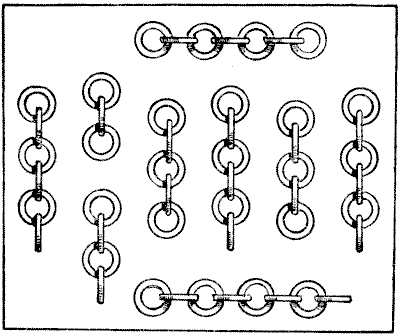    זוהי חידה המבוססת על רעיון נחמד שבו עסק לראשונה מר סם לויד המנוח. לאיש היו תשעה חלקי שרשרת, כפי שמוצג באיור. הוא רצה לחבר את חמישים החוליות האלה לשרשרת אינסופית אחת. יעלה פרוטה לפתוח כל חוליה ושתי פרוטות לרתך חוליה בחזרה, אבל הוא יכול לקנות שרשרת אינסופית חדשה באותו אופי ואיכות עבור `2`s. `2`d. מה היה המהלך הזול ביותר עבורו? אלא אם כן הקורא ערמומי הוא עלול למצוא את עצמו רחוק מהתשובה.

  • שאלה 422 - חידת השבת

    נתקלתי בחידה קטנה זו בספר ישן. אני תוהה כמה קוראים יראו את הפתרון שהמחבר התכוון אליו. 

    הנוצרים את היום הראשון בשבוע כשבת יחזיקו;
    היהודים את השביעי, כפי שעשו מקדמת דנא;
    הטורקים את השישי, כפי שנאמר לנו לעתים קרובות.
    כיצד יכולים שלושתם, באותו מקום ויום,
    שלכל אחד תהיה השבת האמיתית שלו? אמור, אני מתפלל.

  • שאלה 423 - סיכת הָאֹדֶם

    בְּתוֹךְ דַּפֵּי יַעֲקוֹב סְקוֹטְלַנְד יַארְד נִמְצָאִים מִקְרֵי שׁוֹד תַּכְשִׁיטִים מְרַשְּׁמִים, אַךְ אֶחָד הַמְּסֻבָּכִים בְּיוֹתֵר הָיָה גְּנֵבַת הָאֲדָמִים שֶׁל לֵיְדִי לִיטֶלְוּוּד. הָיוּ, כַּמּוּבָן, גְּנֵבוֹת גְּדוֹלוֹת יוֹתֵר בְּמֻנָּחִים שֶׁל עֵרֶךְ, אַךְ מְעַטּוֹת הָיוּ מְפֻתָּלוֹת כָּל כָּךְ. לֵיְדִי לִיטֶלְוּוּד, מֵאֲחֻזַּת רוֹמְלִי, הָיְתָה יְרוּשָׁה יָפָה אַךְ קִיקְיוֹנִית מְעַט בְּצוּרַת סִיכַּת אֹדֶם. בְּעֵת שֶׁשָּׁהֲתָה בְּבֵיתָהּ שֶׁבָּעִיר בִּתְחִלַּת שְׁנוֹת הַשְּׁמוֹנִים הִיא לָקְחָה אֶת הַתַּכְשִׁיט לְחָנוּת בְּבְּרוֹמְפְּטוֹן לְתִקּוּנִים קַלִּים מְעַטִּים.

    "אֹסֶף מְעֻלֶּה שֶׁל אֲדָמִים, גְּבֶרֶת," אָמַר בַּעַל הַחֲנוּת, שֶׁלִּגְבִרְתָּהּ הָיָה זָר.

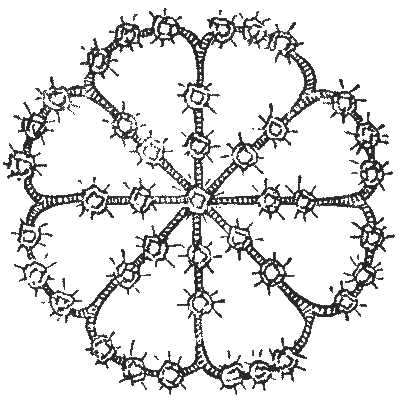
    "כֵּן," הֵשִׁיבָה; "אֲבָל דַּי לִפְלִיאָה כִּי לֹא סָפַרְתִּי אוֹתָם מַמָּשׁ אַף פַּעַם. אִמִּי הִצְבִּיעָה לְפָנַי פַּעַם שֶׁאִם מַתְחִילִים מֵהַמֶּרְכָּז וְסוֹפְרִים קַו אֶחָד לְמַעְלָה, לְאֹרֶךְ הַקָּצֶה וּלְמַטָּה בַּקַּו הַבָּא, תָּמִיד יֵשׁ שְׁמוֹנָה אֲדָמִים. כָּךְ תָּמִיד אֵדַע אִם חֲסֵרָה אֶבֶן.

     

    שִׁשָּׁה חֳדָשִׁים לְאַחַר מִכֵּן אָח שֶׁל לֵיְדִי לִיטֶלְוּוּד, שֶׁחָזַר מֵהָרֶגִימֶנְט שֶׁלּוֹ בְּהוֹדּוּ, שָׂם לֵב שֶׁאֲחוֹתוֹ עוֹנֶדֶת אֶת סִיכַּת הָאֹדֶם בְּאֶחָד הַלֵּילוֹת בְּנֶשֶׁף מְחוֹזִי, וּבַחֲזָרָתָם הַבַּיְתָה בִּקֵּשׁ לְהִסְתַּכֵּל בָּהּ מִקָּרוֹב יוֹתֵר. מִיָּד גִּלָּה אֶת הָעֻבְדָּה שֶׁאַרְבַּע מֵהָאֲבָנִים נֶעֶלְמוּ.

    "אֵיךְ זֶה אֶפְשָׁר?" אָמְרָה לֵיְדִי לִיטֶלְוּוּד. "אִם סוֹפְרִים קַו אֶחָד מֵהַמֶּרְכָּז, לְאֹרֶךְ הַקָּצֶה, וּלְמַטָּה בַּקַּו הַבָּא, בְּכָל כִּוּוּן, תָּמִיד יֵשׁ שְׁמוֹנֶה אֲבָנִים. זֶה תָּמִיד הָיָה כָּךְ וְכָךְ זֶה עַכְשָׁו. אֵיךְ אֵפוֹא אֶפְשָׁר לְהָסִיר אֶבֶן בְּלִי שֶׁאֲגַלֶּה אוֹתָהּ?"

    "שׁוּם דָּבָר לֹא יָכוֹל לִהְיוֹת פָּשׁוּט יוֹתֵר," הֵשִׁיב הָאָח. "אֲנִי מַכִּיר אֶת הַסִּיכָּה הֵיטֵב. בְּמָקוֹר הִיא הִכִּילָה אַרְבָּעִים וְחָמֵשׁ אֲבָנִים, וְעַכְשָׁו יֵשׁ רַק אַרְבָּעִים וְאַחַת. מִישֶׁהוּ גָּנַב אַרְבָּעָה אֲדָמִים, וְאָז הִתְקִין מֵחָדָשׁ מִסְפָּר קָטָן כְּכָל הָאֶפְשָׁר שֶׁל הָאֲחֵרוֹת בְּצוּרָה שֶׁתָּמִיד יִהְיוּ שְׁמוֹנֶה בְּכָל אֶחָד מֵהַכִּוּוּנִים שֶׁצִּיַּנְתְּ."

    לֹא הָיָה סָפֵק קַל שֶׁצּוֹרֵף בְּרוֹמְפְּטוֹן הָיָה הַגַּנָּב, וְהָעִנְיָן הֻנַּח בִּידֵי הַמִּשְׁטָרָה. אֲבָל הָאִישׁ הָיָה דָּרוּשׁ לְגְנֵבוֹת אֲחֵרוֹת, וְעָזַב אֶת הַשְּׁכוּנָה כְּבָר לִפְנֵי זְמַן מָה. עַד הַיּוֹם הַזֶּה הוּא מֵעוֹלָם לֹא נִמְצָא.

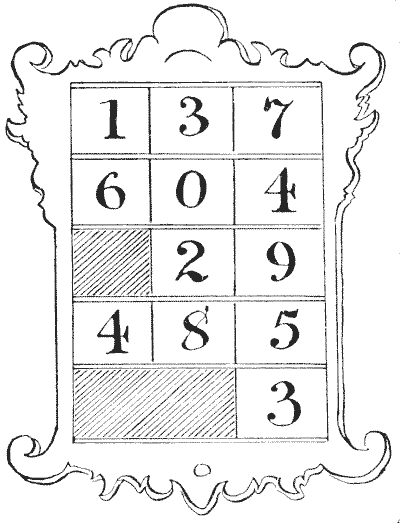
    הַנְּקֻדָּה הַקְּטַנָּה הַמְּעַנְיֶנֶת שֶׁתְּחִלָּה תִּסְכְּלָה אֶת הַמִּשְׁטָרָה, וְשֶׁמְּעַצֶּבֶת אֶת נוֹשֵׂא הַחִידָה שֶׁלָּנוּ, הִיא זוֹ: אֵיךְ סֻדְּרוּ בְּמָקוֹר אַרְבָּעִים וְחָמֵשׁ הָאֲדָמִים עַל הַסִּיכָּה? הַתַּרְשִׁים מַרְאֶה בְּדִיּוּק אֵיךְ סֻדְּרוּ אַרְבָּעִים וְאַחַת לְאַחַר שֶׁחָזְרָה מֵאֵת הַצּוֹרֵף; אֲבָל אַף עַל פִּי שֶׁהֵם סוֹפְרִים שְׁמוֹנֶה נָכוֹן בְּכָל אֶחָד מֵהַכִּוּוּנִים הַמֻּזְכָּרִים, חֲסֵרוֹת אַרְבַּע אֲבָנִים.

  • שאלה 424 - הבלוק המשולב

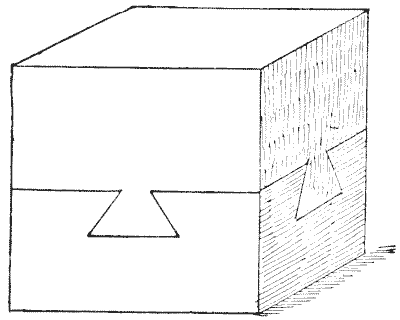    הנה חידה מכנית מוזרה שקיבלתי לפני כמה שנים, אבל אני לא יכול לומר מי המציא אותה לראשונה. היא מורכבת משני גושי עץ מלאים המשולבים זה בזה היטב. בשני הצדדים האנכיים האחרים שאינם נראים, המראה זהה בדיוק לאלה המוצגים. איך חוברו החלקים יחד? כשפרסמתי את החידה הקטנה הזו בעיתון לונדוני קיבלתי (אם כי הם היו לא מוזמנים) די הרבה דגמים, מעץ אלון, מעץ טיק, מהגוני, רוזווד, עץ סאטן, עץ תְרֵשָׁה ועץ אורן; חלקם באורך של חצי רגל, ואחרים בגדלים שונים ממש עד לדגם קטן ועדין בגודל של כחצי אינץ' מרובע. נראה שזה עורר עניין רב.

  • שאלה 425 - ג'ק ועץ השעועית

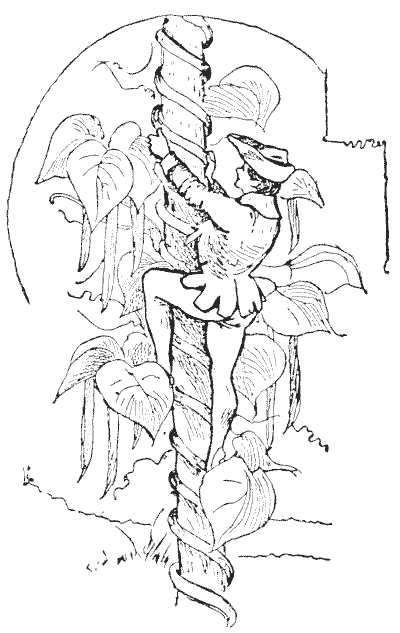    האיור, של אמן בריטי, הוא סקיצה של ג'ק המטפס על עץ השעועית. כעת, האמן עשה טעות חמורה בציור הזה. האם תוכלו לגלות מהי?

  • שאלה 426 - הבעיה של לוח מזמורי התפילה

    ויקאר צ'אמפלי סנט וויניפרד הנכבד נמצא במצוקה רבה. קושי כנסייתי קטן התעורר, ונראה שכל האינטליגנציה המשולבת של הקהילה אינה מסוגלת להתגבר עליו. מה הקושי הזה, אספר בהמשך, אך ייתכן שיוסיף לעניין בבעיה אם אתן תחילה תיאור קצר של המצב המוזר שנוצר. הכל קשור ללוחות מזמורי התפילה של הכנסייה, שהלוחות שלהם ניזוקו כל כך שהם חדלו למלא את המטרה שלשמה הם נועדו. אחד מבני הקהילה הנדיבים הבטיח לשלם עבור סט לוחות חדש בתעריף עלות מסוים; אך מוזר ככל שזה יישמע, לא ניתן להגיע להסכמה לגבי מה צריכה להיות העלות הזו. יצרן הלוחות המוצע נקב במחיר שהתורם מכריז עליו כאבסורדי. הכומר הטוב חושב ששניהם טועים, אז הוא מבקש ממנהל בית הספר לפתור את התרגיל הקטן. אבל האינדיבידואל הזה מצהיר שהוא לא יכול למצוא שום כלל הנוגע לנושא הזה באף אחד מספרי החשבון שלו. לאחר שהוגשה בקשה לרופא המקומי, כאדם בעל אינטלקט ממוצע ומעלה בצ'אמפלי, הוא הבטיח לכומר שהפרקטיקה שלו כה כבדה שאין לו זמן אפילו להסתכל על כך, אם כי עוזרו לוחש שהרופא יושב ער בצורה יוצאת דופן במשך כמה לילות האחרונים. לאלמנה וילסון יש בן חכם, ששמועה אומרת שזכה פעם בפרס על פתרון חידות. הוא טוען מכיוון שהוא לא יכול למצוא שום פתרון לבעיה, זה חייב להיות קשור לריבוע המעגל, הכפלת הקוביה או חלוקת זווית לשלושה; בכל אופן, הוא מעולם לא ראה בעבר חידה על העיקרון, והוא מוותר.

     

    זה היה מצב העניינים כאשר עוזר הכומר (ש, אני חייב לומר, הודה בכנות מההתחלה שמחקר מעמיק בתאולוגיה הוציא מראשו את כל הידע במתמטיקה שהיה לו אי פעם) שלח לי בחביבות את החידה.

    לכנסייה יש שלושה לוחות מזמורים, כל אחד כדי לציין את המספרים של חמישה מזמורים שונים שיש לשיר בתפילה. כל הלוחות נמצאים בשימוש באותה תפילה. ספר המזמורים מכיל `700` מזמורים. נדרש סט מספרים חדש, ואחד מבני הקהילה מציע להגיש סט צבוע על לוחות מתכת, אך מתנה שיירכשו רק המספר הקטן ביותר של לוחות הכרחיים. עלות כל לוח היא `6`d., ועבור צביעת כל לוח החיובים הם: עבור לוח אחד, `1`s.; עבור שני לוחות דומים, `11`¾d. כל אחד; עבור שלושה לוחות דומים, `11`½d. כל אחד, וכן הלאה, כאשר התשלום הוא פרוטה אחת פחות ללוח עבור כל לוח צבוע באופן דומה. עכשיו, מה צריכה להיות העלות הנמוכה ביותר?

    הקוראים ישימו לב שעליהם להשתמש בכל שיטה לגיטימית ומעשית של חיסכון. האיור יבהיר את אופיים של שלושת לוחות המזמורים והלוחות. חמשת המזמורים מצוינים כאן באמצעות שנים עשר לוחות. לוחות אלה מחליקים בנפרד מאחור, ובאיור יש מקום, כמובן, לשלושה לוחות נוספים.

  • שאלה 427 - ציד פזיונים

    חבר קוקני, הנוטה להגזים מאוד, וברור שהוא פחות ספורטאי ממה שהוא טוען, מספר לי את הסיפור הלא מאוד אמין הבא:—

    "זה עתה חזרתי מציד פזיונים עם ידידי הדוכס. היה לנו ספורט נהדר, וביצעתי כמה יריות נפלאות. מה אתה חושב על זה, למשל? אולי תוכל להפוך את זה לחידה. הדוכס ואני חצינו שדה כשפתאום עשרים וארבעה פזיונים התרוממו באוויר ממש לפנינו. יריתי, ושני שלישים מהם נפלו מתים לרגלי. אחר כך הדוכס ירה בשארית, והפיל שלושה חלקי עשרים וארבעה מהם, פצועים בכנף. עכשיו, מתוך אותם עשרים וארבעה ציפורים, כמה עדיין נשארו?"

    נראה שזו שאלה פשוטה למדי, אבל האם הקורא יכול לתת תשובה נכונה?

  • שאלה 428 - הגנן והטבחית

    כתב לי כתב שכינה את עצמו "סיימון הפשוט", והציע שאציג חידת תחבולה מיוחדת בגיליון של השבועון ליום השוטים הבינלאומי, `1900`. אז נתתי את החידה הבאה, והיא גרמה לשעשוע רב; מתוך קהל מתחרים גדול מאוד, רבים מהם מומחים למדי, אף אדם לא פתר אותה, למרות שהיא רצה כמעט חודש.

     

    "האיור הוא סקיצה דמיונית של הכתב שלי, 'סיימון הפשוט,' מנסה לפתור את החידה האריתמטית הקטנה והתמימה הבאה. מרוץ בין גבר לאישה שהייתי עד לו באחד מיום השוטים הבינלאומי נחקק בזיכרוני. זה קרה באחוזה כפרית, שם הגנן והטבחית החליטו לרוץ לתחרות לנקודה במרחק של `100` רגל ישר וחזרה. גיליתי שהגנן רץ `3` רגל בכל צעד והטבחית רק `2` רגל, אבל אז היא עשתה שלושה צעדים לשני הצעדים שלו. עכשיו, מה הייתה תוצאת המירוץ?"

    שבועיים לאחר הפרסום הוספתי את ההערה הבאה: "הועלתה ההצעה שאולי יש תחבולה ב'חזרה', אבל אין כזו. המירוץ הוא לנקודה במרחק `100` רגל וחזרה הביתה—כלומר, מרחק של `200` רגל. כתב אחד שואל האם לוקח להם בדיוק אותו זמן להסתובב, ואני משיב שכן. נראה שאחר חושד שזה בעצם חידה, והתשובה היא ש'תוצאת המירוץ הייתה תיקו (נישואין)'. אבל לא הייתה לי כוונה כזו. החידה היא אריתמטית, כפי שהיא מתיימרת להיות."

  • שאלה 429 - הנחת מטבעות חצי פני

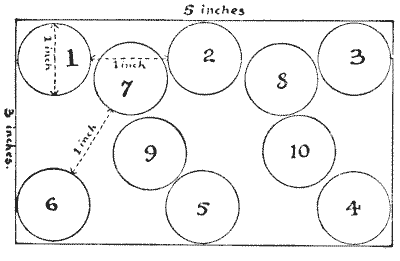    הנה חידה קטנה ומעניינת שהוצעה לי על ידי מר וו. טי. וויט. סמנו על דף נייר שטח מלבני של `5` אינץ' על `3` אינץ', ואז מצאו את המספר הגדול ביותר של מטבעות חצי פני שניתן להניח בתוך המתחם בתנאים הבאים. קוטר של מטבע חצי פני הוא בדיוק אינץ' אחד. הניחו את מטבע חצי הפני הראשון שלכם היכן שתרצו, ואז הניחו את המטבע השני בדיוק במרחק של אינץ' אחד מהראשון, את השלישי במרחק של אינץ' אחד מהשני, וכן הלאה. אסור לאף מטבע חצי פני לגעת במטבע אחר או לחצות את הגבול. האיור שלנו יבהיר את העניין בצורה מושלמת. מטבע מספר `2` נמצא במרחק אינץ' אחד ממספר `1`; מספר `3` במרחק אינץ' אחד ממספר `2`; מספר `4` במרחק אינץ' אחד ממספר `3`; אבל אחרי שמניחים את מספר `10`, איננו יכולים להתקדם בניסיון זה. עם זאת, אפשר היה להכניס עוד כמה מטבעות חצי פני. כמה יכול הקורא להניח?

  • שאלה 430 - מצא את אשת האיש

     

    יום אחד בקיץ בשנת `1903` הסתובבתי לאורך חזית ברייטון, צופה באנשים המטיילים על החוף, כאשר ידידי שליווה אותי משך לפתע את תשומת ליבי לאדם שעמד לבדו, ואמר, "האם תוכל להצביע על אשת האיש הזה? הם שוהים באותו מלון כמוני, והגברת היא אחת מאלה שנראות." לאחר מספר דקות של תצפית, הצלחתי לציין את הגברת בצורה נכונה. ידידי היה סקרן לדעת באיזו שיטת חשיבה הגעתי לתוצאה. זו הייתה תשובתי:—

    "אנו יכולים מיד להוציא מהכלל את אחות הרחמניות ואת הילדה בשמלה הקצרה; גם את האישה המוכרת תפוזים. זו לא יכולה להיות הגברת בבגדי אלמנות. זו לא הגברת בכיסא הגלגלים, כי היא לא שוהה במלון שלך, כי במקרה ראיתי אותה יוצאת מבית פרטי הבוקר בסיוע המשרתת שלה. שתי הנשים באדום סעדו ארוחת בוקר במלון שלי הבוקר, ומכיוון שלא לבשו בגדי חוץ, אני מסיק שהן שוהות שם. לכן זה נשען בין הגברת בכחול לזו עם השמשייה הירוקה. אבל היד השמאלית שמחזיקה את השמשייה היא, אתה רואה, לא מכוסה בכפפה ואין עליה טבעת נישואין. כתוצאה מכך, אני נאלץ למסקנה שהגברת בכחול היא אשת האיש הזה—ואתה אומר שזה נכון."

    כעת, מכיוון שידידי היה אמן, ומכיוון שחשבתי שאפשר להמציא חידה משעשעת על פי קווי השאלה שלו, ביקשתי ממנו להכין לי ציור לפי כמה הנחיות שנתתי לו, ויש לי תענוג להציג את התוצרת שלו לקוראים שלי. ניתן לראות שהתמונה מציגה שישה גברים ושש נשים: מס' `1, 3, 5, 7, 9` ו-`11` הן נשים, ומס' `2, 4, 6, 8, 10` ו-`12` הם גברים. שנים עשר האנשים האלה מייצגים שישה זוגות נשואים, שכולם זרים זה לזה, אשר, בהליכה חסרת מטרה, התערבבו. אבל אנחנו עוסקים רק באיש שחובש כובע קש—מספר `10`. החידה היא למצוא את אשת האיש הזה. בחנו את שש הנשים בקפידה, ובדקו אם תוכלו לקבוע מי מהן.

    הצגתי את התמונה באותה תקופה לכמה חברים, והם הביעו דעות שונות מאוד בנושא. אחד אמר, "אני לא מאמין שהוא יתחתן עם בחורה כמו מספר `7`." אחר אמר, "אני בטוח שבחורה נחמדה כמו מספר `3` לא תתחתן עם בחור כזה!" אחר אמר, "זה חייב להיות מספר `1`, כי היא התרחקה ככל האפשר מהבהמה!" הוצע שוב, שזה חייב להיות מספר `11`, כי "נראה שהוא מסתכל לעברה;" אבל ציניקן השיב, "בגלל אותה סיבה, אם הוא באמת מסתכל עליה, אני צריך לומר שהיא לא אשתו!"

    אני משאיר כעת את השאלה בידי הקוראים שלי. מי באמת אשתו של מספר `10`?

    האיור מצומצם בהכרח מאוד מהקנה מידה הגדול שבו הוא הופיע במקור בThe Weekly Dispatch (24 במאי `1903`), אך יש לקוות שהפרטים יהיו ברורים דיים כדי לאפשר לקורא להפיק בידור מבחינתו. בכל מקרה, הפתרון הניתן יאפשר לו לעקוב אחר הנקודות בעניין.