שעשועונים במתמטיקה, הנרי ארנסט דודני

  • שאלה 201 - איך ליצור בורות מים

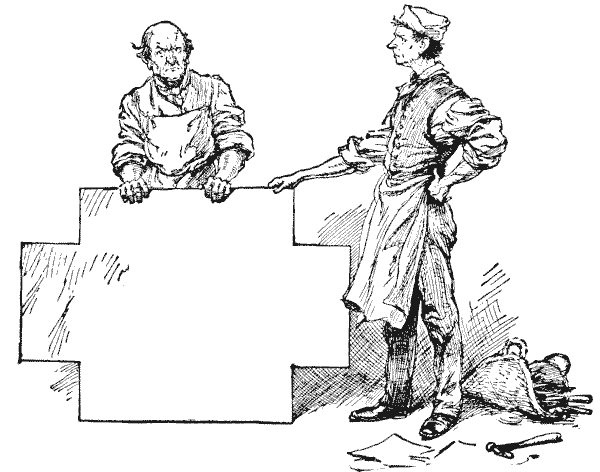    לידידנו באיור יש יריעת אבץ גדולה, שממדיה (לפני החיתוך) שמונה רגל על שלוש רגל, והוא חתך פיסות מרובעות (כולן באותו גודל) מארבע הפינות וכעת הוא מציע לקפל את הצדדים, להלחים את הקצוות, ולהכין בור מים. אבל הנקודה שמבלבלת אותו היא זו: האם הוא חתך את פיסות הריבוע בגודל הנכון, כך שהבור יכיל את הכמות הגדולה ביותר האפשרית של מים? אתם רואים, אם חותכים אותם קטנים מאוד, מקבלים בור רדוד מאוד; אם חותכים אותם גדולים, מקבלים בור גבוה וצר. הכל עניין של למצוא דרך לחתוך את ארבע פיסות הריבוע האלה בדיוק בגודל הנכון. איך נוכל להימנע מלחתוך אותם קטנים מדי או גדולים מדי?

  • שאלה 202 - חידת החרוט

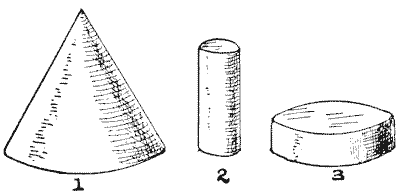    יש לי חרוט עץ, כפי שמוצג באיור `1`. איך עליי לחתוך ממנו את הגליל הגדול ביותר האפשרי? ניתן לראות שאני יכול לחתוך אחד שהוא ארוך ודק, כמו באיור `2`, או קצר ועבה, כמו באיור `3`. אבל אף אחד מהם אינו הגדול ביותר האפשרי. ילד יכול לומר לכם היכן לחתוך, אם הוא היה מכיר את הכלל. האם תוכלו למצוא את הכלל הפשוט הזה?

  • שאלה 203 - בעניין גלגלים

     

    ישנן מספר עובדות מוזרות הנוגעות לתנועת גלגלים אשר עשויות לבלבל את המתחילים. לדוגמה: כאשר רכבת נוסעת מלונדון לקרו, חלקים מסוימים ברכבת, בכל רגע נתון, נעים למעשה מקרו לכיוון לונדון. האם תוכלו לציין את החלקים האלה? זה נראה אבסורדי שחלקים מאותה רכבת יכולים בכל זמן נתון לנוע בכיוונים מנוגדים, אך כך הם פני הדברים.

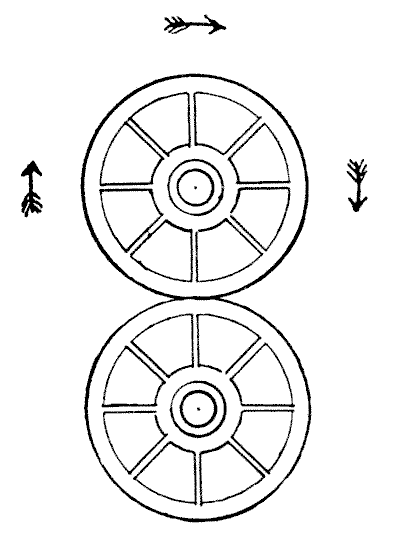
    באיור המצורף יש לנו שני גלגלים. הגלגל התחתון אמור להיות קבוע והגלגל העליון מסתובב סביבו בכיוון החצים. עכשיו, כמה פעמים הגלגל העליון מסתובב סביב צירו שלו במהלך סיבוב שלם סביב הגלגל השני? אל תמהרו עם התשובה, אחרת כמעט בטוח שתטעו. נסו זאת עם שני מטבעות על השולחן והתשובה הנכונה תפתיע אתכם, כשתצליחו לראות אותה.

  • שאלה 204 - חידת גפרורים חדשה

    באיור מוצגים שמונה-עשר גפרורים המסודרים כך שהם תוחמים שני שטחים, כאשר אחד גדול פי שניים מהשני. האם תוכלו לסדר אותם מחדש (`1`) כך שיתחמו שני שטחים מרובעים, כאשר אחד גדול בדיוק פי שלושה מהשני, ו- (`2`) כך שיתחמו שני שטחים מחומשים, כאשר אחד גדול בדיוק פי שלושה מהשני? יש להשתמש בכל שמונה-עשר הגפרורים בצורה הוגנת בכל מקרה; שני השטחים חייבים להיות מופרדים לחלוטין, ולא צריכים להיות קצוות רופפים או גפרורים כפולים.

  • שאלה 205 - מִכְלְאוֹת שֵׁשׁ הַכְּבָשִׂים

     

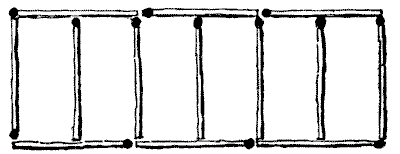
    הִנֵּה חִידָה קְטַנָּה חֲדָשָׁה עִם גּוּפְרִיתִים. כְּפִי שֶׁנִּיתָן לִרְאוֹת בְּאִיּוּר, שְׁלוֹשָׁה עָשָׂר גּוּפְרִיתִים, הַמְּיַצְּגִים מַעֲבָרִים שֶׁל חוֹלֵף, מֻנָּחִים כָּךְ שֶׁהֵם תּוֹחֲמִים שֵׁשׁ מִכְלְאוֹת כְּבָשִׂים בְּאוֹתוֹ גֹּדֶל. עַכְשָׁו, אֶחָד מִמַּעֲבָרִים אֵלֶּה נִגְנַב, וְהַחוֹלֵף עֲדַיִן רָצָה לִתְחוֹם שֵׁשׁ מִכְלָאוֹת בְּגֹּדֶל שָׁוֶה עִם שְׁנֵים עָשָׂר הַגּוּפְרִיתִים שֶׁנִּשְׁאֲרוּ. אֵיךְ הוּא הָיָה צָרִיךְ לַעֲשׂוֹת אֶת זֶה? יֵשׁ לְהִשְׁתַּמֵּשׁ בְּהֶגְיוֹן בְּכָל שְׁנֵים הֶעָשָׂר הַגּוּפְרִיתִים, וְלֹא צְרִיכִים לִהְיוֹת גּוּפְרִיתִים כְּפוּלִים אוֹ קְצוֹת רוֹפְפִים.

  • שאלה 206 - המלך והמבצרים

    היה היה, בעת העתיקה, מלך חזק, שהיו לו רעיונות מוזרים בנושא האדריכלות הצבאית. הוא טען שיש כוח וחיסכון גדולים בצורות סימטריות, ותמיד ציטט את דוגמת הדבורים, שבונות את החלות שלהן בתאים משושים מושלמים, כדי להוכיח שיש לו את הטבע שתומך בו. הוא החליט לבנות עשרה מבצרים חדשים במדינתו, שכולם יהיו מחוברים בחומות מבוצרות, שייצרו חמישה קווים עם ארבעה מבצרים בכל קו. האדריכל המלכותי הציג את תוכניתו המקדימה בצורה שהראיתי. אבל המלך הצביע על כך שניתן לגשת לכל מבצר מבחוץ, וציווה שהתוכנית תשונה כך שכמה שיותר מבצרים יהיו חופשיים מתקיפה מבחוץ, וניתן יהיה להגיע אליהם רק על ידי חציית החומות המבוצרות. האדריכל השיב שהוא חושב שאי אפשר לסדר אותם כך שאפילו מבצר אחד, שהמלך הציע להשתמש בו כמגורים מלכותיים, יהיה מוגן כל כך, אבל הוד מלכותו עד מהרה הבהיר לו כיצד ניתן לעשות זאת. איך הייתם בונים את עשרת המבצרים והביצורים כדי למלא בצורה הטובה ביותר את דרישות המלך? זכרו שהם חייבים ליצור חמישה קווים ישרים עם ארבעה מבצרים בכל קו.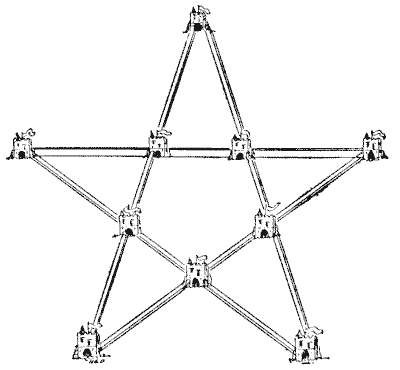

  • שאלה 207 - דובדבנים ושזיפים

    האיור הוא תוכנית של קוטג' כפי שהוא עומד מוקף במטע של חמישים וחמישה עצים. עשרה מהעצים הללו הם דובדבנים, עשרה הם שזיפים, והשאר תפוחים. הדובדבנים נשתלו כך שייצרו חמישה קווים ישרים, עם ארבעה עצי דובדבן בכל קו. עצי השזיף נשתלו גם הם כך שייצרו חמישה קווים ישרים עם ארבעה עצי שזיף בכל קו. החידה היא להראות אילו הם עשרת עצי הדובדבן ואילו הם עשרת עצי השזיף. על מנת שלדובדבנים ולשזיפים יהיה את הנוף הטוב ביותר, כמה שפחות (בתנאים הקיימים) נשתלים בצד הצפוני והמזרחי של המטע. כמובן שבהוצאת קבוצה של עשרה עצים (דובדבן או שזיף, לפי העניין) מתעלמים מכל העצים המפרידים. זאת אומרת, ארבעה עצים יכולים להיות בקו ישר ללא קשר לעצים אחרים (או לבית) שנמצאים ביניהם. אחרי החידה האחרונה זה יהיה די קל.

  • שאלה 208 - חידת מטעים

    לאיש היתה חלקת אדמה מרובעת עם ארבעים ותשעה עצים, אך, כפי שניתן לראות מההשמטות באיור, ארבעה עצים נפלו וסולקו. כעת הוא רוצה לכרות את כל היתר מלבד עשרה עצים, שאותם יש להשאיר כך שהם ייצרו חמש שורות ישרות עם ארבעה עצים בכל שורה. אילו הם עשרת העצים שעליו להשאיר?

  • שאלה 209 - עשרים ואחד עצים

    אדון רצה לשתול עשרים ואחד עצים בפארק שלו כך שהם ייצרו שתים עשרה שורות ישרות עם חמישה עצים בכל שורה. האם הייתם יכולים לספק לו סידור סימטרי נאה שיעמוד בתנאים אלה?

  • שאלה 210 - עשרת המטבעות

    הניחו עשרה מטבעות פני על גיליון נייר או קרטון גדול, כפי שמוצג בתרשים, חמישה על כל קצה. כעת הסירו ארבעה מהמטבעות, מבלי להפריע לאחרים, והחזירו אותם לנייר כך שעשרת המטבעות ייצרו חמישה קווים ישרים עם ארבעה מטבעות בכל קו. זה כשלעצמו אינו קשה, אבל עליכם לנסות לגלות בכמה דרכים שונות ניתן לפתור את החידה, בהנחה שבכל מקרה שתי השורות בהתחלה זהות לחלוטין.