שעשועונים במתמטיקה, הנרי ארנסט דודני

• שאלה 411 - ריבוע קסם של מספרים מורכבים

  כפי שדנו זה עתה בבניית ריבועי קסם עם מספרים ראשוניים, הבעיה הבאה מהווה בעיה נלווית מעניינת. בנו ריבוע קסם עם תשעה מספרים מורכבים עוקבים - הקטן ביותר האפשרי.
  נושאים:

  תורת המספרים -> מספרים ראשוניים

• שאלה 412 - מסע הפרש הקסום

  הנה בעיה שעדיין לא נפתרה, וגם לא הוכחה אי-אפשרותה. שחקו עם הפרש פעם אחת בכל משבצת בלוח השחמט במסע שלם, ספרו את המשבצות לפי סדר הביקור, כך שכאשר תושלם, הריבוע יהיה "קסום," ויסתכם ל-`260` בכל טור, בכל שורה ובכל אחד משני האלכסונים הארוכים. אתן את התשובה הטובה ביותר שהצלחתי להשיג, שבה יש טעות קלה באלכסונים בלבד. האם ניתן למצוא פתרון מושלם? אני משוכנע שאי אפשר, אבל זו רק "דעה נלהבת."

  נושאים:

  לוגיקה קומבינטוריקה -> טבלאות מספריות קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות

• שאלה 413 - כשל לוח שחמט

   

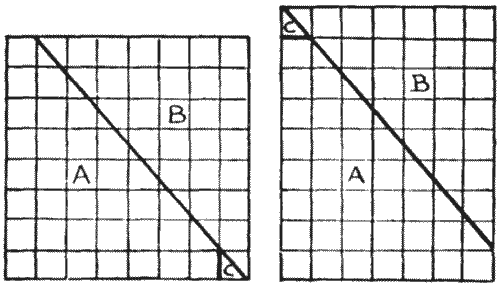
  "הנה דיאגרמה של לוח שחמט," הוא אמר. "אתם רואים שיש שישים וארבעה ריבועים—שמונה על שמונה. עכשיו אני מצייר קו ישר מהפינה השמאלית העליונה, היכן שהריבוע הראשון והשני נפגשים, אל הפינה הימנית התחתונה. אני גוזר לאורך הקו הזה עם המספריים, מחליק למעלה את החלק שסימנתי B, ואז גוזר את הפינה הקטנה C על ידי חיתוך לאורך הקו הישר הראשון. החלק הקטן הזה יתאים בדיוק למקומו למעלה, ועכשיו יש לנו מלבן עם שבעה ריבועים מצד אחד ותשעה ריבועים מצד שני. לכן, יש עכשיו רק שישים ושלושה ריבועים, מכיוון ששבע כפול תשע יוצר שישים ושלוש. לאן לעזאזל נעלם הריבוע האבוד הזה? ניסיתי שוב ושוב לתפוס את הקטן המנוול, אבל הוא תמיד מתחמק ממני. בשביל החיים שלי אני לא מצליח לגלות איפה הוא מסתתר."

  "זה נראה כמו הכשל הישן האחר של לוח השחמט, ואולי ההסבר זהה," אמר רג'ינלד—"שהחלקים לא מתאימים בדיוק."

  "אבל הם כן מתאימים," אמר הדוד ג'ון. "נסה את זה, ותראה."

  מאוחר יותר באותו ערב נראו רג'ינלד וג'ורג' בפינה כשהראשים שלהם ביחד, מנסים לתפוס את הריבוע הקטן החמקמק הזה, וזה רק הוגן לציין שלפני שהם פרשו ללילה הם הצליחו לתפוס את הטרף שלהם, אם כי חלק מחברי החברה לא הצליחו לראות אותו כשנתפס. האם הקורא יכול לפתור את התעלומה הקטנה?

  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה

• שאלה 414 - מי היה הראשון?

  אנדרסון, ביגס וקרפנטר שהו יחד במקום ליד הים. יום אחד הם יצאו בסירה והיו במרחק מייל אחד מהחוף כאשר נורתה רובה לעברם. מדוע או על ידי מי נורתה הירייה למרבה המזל לא מעניין אותנו, מכיוון שאין מידע על נקודות אלה, אך מהעובדות שאספתי נוכל להשיג חומר לפאזל קטן וסקרן למתחילים.

  נראה שאנדרסון רק שמע את קול הירי, ביגס רק ראה את העשן, וקרפנטר רק ראה את הכדור פוגע במים לידם. כעת, עולה השאלה: מי מהם ידע ראשון על ירי הרובה?

  נושאים:

  לוגיקה -> הגיון

• שאלה 415 - כפר נפלא

  ישנו כפר מסוים ביפן, השוכן בעמק נמוך מאוד, ובכל זאת השמש קרובה יותר לתושבים בכל צהריים, ב-`3,000` מיילים ומעלה, מאשר כשהיא זורחת או שוקעת עבור אנשים אלה. באיזה חלק של המדינה ממוקם הכפר?

• שאלה 416 - חידת לוח שנה

  אם סוף העולם יגיע ביום הראשון של מאה חדשה, האם תוכל לומר מה הסיכויים שזה יקרה ביום ראשון?
  נושאים:

  תורת המספרים -> חשבון השאריות -> סימני חלוקה

• שאלה 417 - טבעות הברזל המייגעות

   

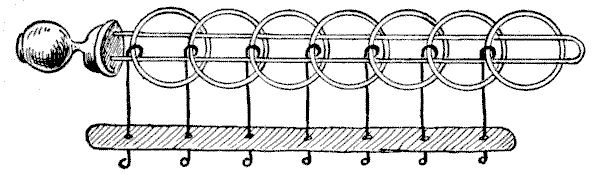
  האיור מייצג אחד מהחידות המכאניות העתיקות ביותר. מקורו אינו ידוע. קרדנו, המתמטיקאי, כתב עליו בשנת `1550`, וואליס בשנת `1693`; בעוד שאומרים שהוא עדיין נמצא בכפרים אנגליים נידחים (לפעמים מונח במקומות מוזרים, כמו מגדל פעמונים של כנסייה), עשוי מברזל, ונקרא באופן הולם "טבעות מייגעות", ומשמש את הנורווגים כיום כמנעול לקופסאות ותיקים. בחנויות הצעצועים הוא נקרא לפעמים "טבעות סיניות", אם כי נראה שאין סמכות לתיאור, ולרוב הוא מכונה בשם הלא מספק "הטבעות המבלבלות". הצרפתים קוראים לזה "Baguenaudier."

  ניתן לראות שהחידה מורכבת מ-לולאה פשוטה של חוט המקובעת בידית שאותה מחזיקים ביד שמאל, וממספר מסוים של טבעות המאובטחות על ידי חוטים העוברים דרך חורים ב-מוט ונשמרים שם על ידי קצותיהם הקהים. החוטים פועלים בחופשיות במוט, אך אינם יכולים להיפרד ממנו, וגם לא ניתן להסיר את החוטים מהטבעות. החידה הכללית היא לנתק את הלולאה לחלוטין מכל הטבעות, ואז להחזיר את כולן שוב.

  כעת, ניתן לראות במבט חטוף שניתן להסיר את הטבעת הראשונה (מימין) בכל עת על ידי החלקתה מעל הקצה והשלכתה דרך הלולאה; או שאפשר להחזיר אותה על ידי היפוך הפעולה. מלבד זאת, הטבעת היחידה שניתן להסיר אי פעם היא זו שבמקרה נמצאת השנייה הסמוכה על הלולאה בקצה הימני. כך, כשכל הטבעות עליה, ניתן להפיל את השנייה מיד; כשהטבעת הראשונה למטה, אינך יכול להפיל את השנייה, אך תוכל להסיר את השלישית; כששלוש הטבעות הראשונות למטה, אינך יכול להפיל את הרביעית, אך תוכל להסיר את החמישית; וכן הלאה. יתברר שאפשר להפיל את הטבעות הראשונה והשנייה יחד או להחזיר אותן יחד; אך כדי למנוע בלבול, לא נאפשר את המהלך הכפול החריג הזה, ונגיד שניתן להחזיר או להסיר רק טבעת אחת בכל פעם.

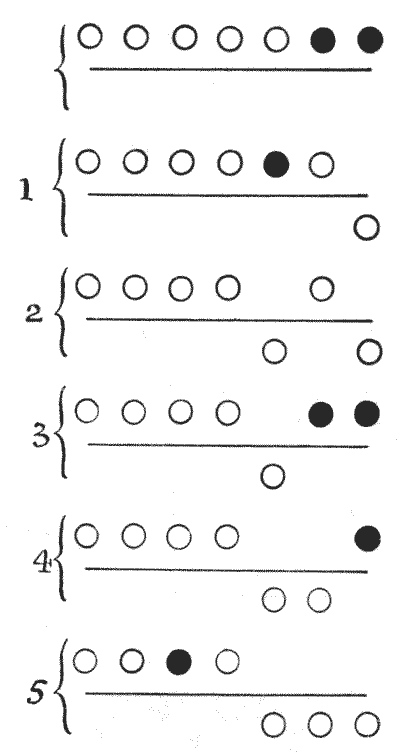
  אנו יכולים להסיר טבעת אחת ב-`1` מהלך; שתי טבעות ב-`2` מהלכים; שלוש טבעות ב-`5` מהלכים; ארבע טבעות ב-`10` מהלכים; חמש טבעות ב-`21` מהלכים; ואם נמשיך להכפיל (ולהוסיף אחד כאשר מספר הטבעות הוא אי-זוגי) נוכל לברר בקלות את מספר המהלכים להסרת כל מספר טבעות לחלוטין. כדי להוריד את כל שבע הטבעות נדרשים `85` מהלכים. בואו נסתכל על חמשת המהלכים שנעשו בהסרת שלוש הטבעות הראשונות, העיגולים מעל הקו מייצגים טבעות על הלולאה ואלה שמתחת מייצגים טבעות מחוץ ללולאה.

  הפילו את הטבעת הראשונה; הפילו את השלישית; הרימו את הראשונה; הפילו את השנייה; והפילו את הראשונה—`5` מהלכים, כפי שמוצג בבירור בתרשימים. העיגולים הכהים מראים בכל שלב, ממצב ההתחלה ועד הסיום, אילו טבעות אפשר להפיל. לאחר מהלך `2` יורגש שלא ניתן להפיל אף טבעת עד שאחת תוחזר, מכיוון שהטבעות הראשונה והשנייה מימין שנמצאות כעת על הלולאה אינן יחד. לאחר המהלך החמישי, אם ברצוננו להסיר את כל שבע הטבעות, עלינו כעת להפיל את החמישית. אבל לפני שנוכל להסיר אז את הרביעית, יש צורך להחזיר את שלוש הראשונות ולהסיר את שתי הראשונות. אז יהיו לנו `7, 6, 4, 3` על הלולאה, ולכן נוכל להפיל את הרביעית. כשנחזיר `2` ו-`1` ונסיר `3, 2, 1`, נוכל להפיל את הטבעת השביעית. הפעולה הבאה אז תהיה להשיג `6, 5, 4, 3, 2, 1` על הלולאה ולהסיר `4, 3, 2, 1`, ואז `6` תרד; ואז להשיג `5, 4, 3, 2, 1` על הלולאה, ולהסיר `3, 2, 1`, ואז `5` תרד; ואז להשיג `4, 3, 2, 1` על הלולאה ולהסיר `2, 1`, ואז `4` תרד; ואז להשיג `3, 2, 1` על הלולאה ולהסיר `1`, ואז `3` תרד; ואז להשיג `2, 1` על הלולאה, ואז `2` תרד; ו-`1` תיפול דרך במהלך ה-85, ותשאיר את הלולאה חופשית לחלוטין. על הקורא להיות מסוגל כעת להבין את החידה, בין אם יש לו אותה ביד בצורה מעשית ובין אם לא.

   

  הבעיה המסוימת שאני מציע היא פשוט זו. נניח שיש בסך הכל ארבע עשרה טבעות על טבעות הברזל המייגעות, ואנו ממשיכים להסיר את כולן בצורה הנכונה כדי לא לבזבז אף מהלך. מה יהיה מצב הטבעות לאחר שבוצע המהלך ה-`9`,999?

  נושאים:

  אריתמטיקה תורת המספרים -> חלוקה -> זוגיות אלגברה -> סדרות -> נוסחאות נסיגה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים

• שאלה 418 - עלייה במדרגות כזו

  בווילה פרברית יש גרם מדרגות קטן עם שמונה מדרגות, לא כולל משטח הנחיתה. החידה הקטנה שבה טומי סמארט הדהים את משפחתו היא זו. עליכם להתחיל מלמטה ולנחות פעמיים על הרצפה מעל (ולעצור שם בסיום), לאחר שחזרתם פעם אחת לקומת הקרקע. אבל עליכם להקפיד להשתמש בכל מדרגה אותו מספר פעמים. בכמה צעדים מעטים תוכלו לבצע את העלייה? זה נראה עניין פשוט מאוד, אבל סביר להניח שבניסיון הראשון שלכם תעשו הרבה יותר צעדים מהנדרש. כמובן שאסור לכם לעלות יותר ממדרגה אחת בכל פעם.

  טומי מכיר את הטריק, והראה אותו לאביו, שמצהיר על בוז לדברים כאלה; אבל כשהילדים במיטה, האב לוקח לעתים קרובות חברים למסדרון ונהנה מצחוק טוב על הבלבול שלהם. ובכל זאת, הכל כל כך פשוט כשאתה יודע איך זה נעשה.

  נושאים:

  אריתמטיקה אלגברה -> בעיות מילוליות אלגברה -> סדרות

• שאלה 419 - חמש פרוטות

  הנה חידה קשה במיוחד, ולמרות זאת התנאים שלה פשוטים באופן מגוחך. כל קורא יודע איך להניח ארבע פרוטות כך שהן יהיו במרחק שווה זו מזו. כל שעליכם לעשות הוא לסדר שלוש מהן שטוחות על השולחן כך שהן יגעו זו בזו בצורת משולש, ולהניח את הפרוטה הרביעית מעל במרכז. אז, מכיוון שכל פרוטה נוגעת בכל פרוטה אחרת, כולן נמצאות במרחקים שווים זו מזו. עכשיו נסו לעשות את אותו הדבר עם חמש פרוטות - הניחו אותן כך שכל פרוטה תיגע בכל פרוטה אחרת - ותגלו שזה עניין שונה לחלוטין.
  נושאים:

  גאומטריה -> גאומטריה במרחב

• שאלה 420 - תולעת הספרים החרוצה

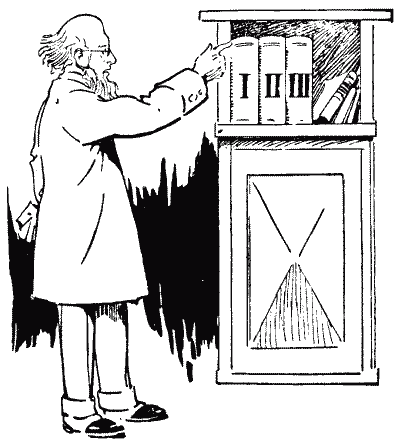  ידידנו, פרופסור ראקבריין, נראה באיור כשהוא מציג עוד אחת מהחידות הקטנות שלו. הוא מסביר שמאז הפעם האחרונה שהוא נאלץ להוריד את שלושת הכרכים האלה של ספר מלומד ממקומם על המדפים שלו, תולעת ספרים קדחה למעשה חור ישר מהעמוד הראשון עד האחרון. הוא אומר שהעלים הם בעובי שלושה אינץ' בכל כרך, וכל כריכה היא בדיוק שמינית אינץ' בעובי, והוא שואל כמה ארוכה הייתה המנהרה שהתולעת החרוצה הייתה צריכה לקדוח בהכנת רכבת הצינור החדשה שלה. האם אתה יכול לספר לו?
  נושאים:

  אלגברה -> בעיות מילוליות