שעשועונים במתמטיקה, הנרי ארנסט דודני

  • שאלה 211 - תריסר פשטידות בשר

    ניתן לראות באיור שלנו כיצד ניתן להניח תריסר פשטידות בשר על השולחן כך שייצרו שש שורות ישרות עם ארבע פשטידות בכל שורה. החידה היא להסיר רק ארבע מהן למיקומים חדשים כך שיהיו שבע שורות ישרות עם ארבע בכל שורה. אילו ארבע הייתם מסירים, והיכן הייתם מחליפים אותן?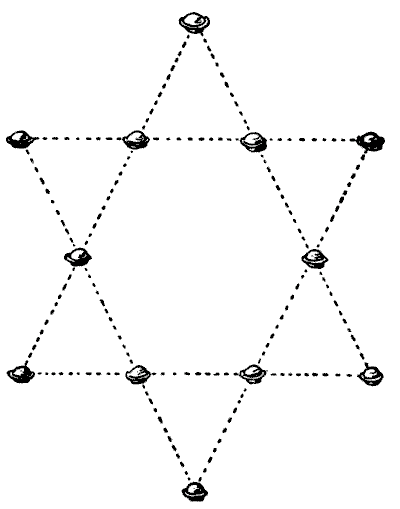

  • שאלה 212 - מטע בבורמה

    לפני זמן קצר קיבלתי מכתב מעניין מהכומר הבריטי במייקטילה, בורמה העליונה, בו כתב לי הכומר שנהנה באונייה בדרכו לשם לנסות לפתור את החידה הקטנה הזו.

     

    אם יש לו מטע של ארבעים ותשעה עצים, נטועים בצורת ריבוע כפי שמוצג באיור המצורף, הוא רוצה לדעת איך הוא יכול לכרות עשרים ושבעה מהעצים כך שעשרים ושניים העצים שיישארו יעמדו בשורות רבות ככל האפשר עם ארבעה עצים בכל שורה.

    כמובן שלא יכולים להיות יותר מארבעה עצים בשורה.

  • שאלה 213 - טורקים ורוסים

    חידה זו היא בסגנון בעיית האפרידי שפורסמה על ידי ב-Tit-Bits לפני כמה שנים.

    על שטח מישורי פתוח, קבוצת חיילי רגלים רוסים, שאף אחד מהם לא הוצב באותו מקום, הופתעה לפתע על ידי שלושים ושניים טורקים, שפתחו באש על הרוסים מכל הכיוונים. כל אחד מהטורקים ירה בו זמנית כדור, וכל כדור חלף מיד מעל ראשיהם של שלושה חיילים רוסים. מכיוון שכל אחד מהכדורים הללו הרג אדם אחר, החידה היא לגלות מהו המספר הקטן ביותר האפשרי של חיילים שהקבוצה הרוסית יכולה הייתה להכיל ומה היו האבדות בכל צד.

  • שאלה 214 - שש הצפרדעים

    שש הצפרדעים המשכילות באיור אומנו להפוך את סדרן, כך שהמספרים שלהן יהיו `6, 5, 4, 3, 2, 1`, כאשר הריבוע הריק נמצא במיקומו הנוכחי. הן יכולות לקפוץ למשבצת הבאה (אם היא פנויה) או לדלג מעל צפרדע אחת למשבצת הבאה מעבר לה (אם היא פנויה), בדיוק כפי שאנו נעים במשחק הדמקה, ויכולות לנוע אחורה או קדימה כרצונן. האם תוכלו להראות כיצד הן מבצעות את המשימה שלהן במספר המהלכים המועט ביותר האפשרי? זה די קל, אז כשסיימתם הוסיפו צפרדע שביעית מימין ונסו שוב. לאחר מכן הוסיפו עוד צפרדעים עד שתוכלו לתת את הפתרון הקצר ביותר עבור כל מספר. כי זה תמיד אפשרי, עם המשבצת הריקה הבודדת הזו, לא משנה כמה צפרדעים יש.

  • שאלה 215 - חידת החגב

    הועלתה סברה שהחידה הזו הייתה חביבה מאוד על החניכים הצעירים של הסיטי של לונדון במאות השש-עשרה והשבע-עשרה. הקוראים בוודאי הבחינו בחגב הפליז המוזר בבורסה המלכותית. יצור ארוך שנים זה ניצל משריפות `1666` ו-`1838`. החגב, כדרכו, היה סמל של סר תומס גרשם, סוחר מכולת, שמת בשנת `1579`, ומסיבה זו הוא שימש כסמל על ידי מכולת באופן כללי. למרבה הצער עבור האגדה לגבי מקורה, החידה הופקה על ידי עצמי רק בשנת `1900`. על שנים עשר מתוך שלושה עשר הדיסקים השחורים מונחים אסימונים ממוספרים או חגבים. החידה היא להפוך את סדרם, כך שיקראו, `1, 2, 3, 4` וכו', בכיוון ההפוך, כאשר הדיסק הריק נשאר באותו מיקום כמו עכשיו. הזיזו אחד בכל פעם בכל סדר, או לדיסק הריק הסמוך או על ידי קפיצה מעל חגב אחד, כמו המהלכים בדמקה. ניתן לבצע את המהלכים או הקפיצות בכל כיוון שאפשרי בכל עת. מהם מספר המהלכים המועט ביותר שבו ניתן לעשות זאת?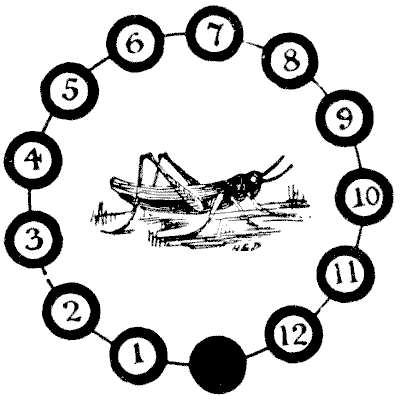

  • שאלה 216 - הצפרדעים המשכילות

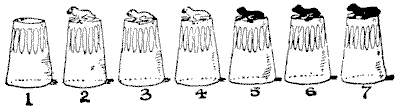    שש הצפרדעים המשכילות שלנו למדו תעלול חדש ויפה. כאשר מניחים אותן על כוסות זכוכית, כפי שמוצג באיור, הן מחליפות צדדים כך ששלוש השחורות נמצאות משמאל והצפרדעים הלבנות מימין, כאשר הכוס הריקה בקצה הנגדי - מס' `7`. הן יכולות לקפוץ לכוס הבאה (אם היא ריקה), או מעל צפרדע אחת, או שתיים, לכוס ריקה. ניתן לבצע את הקפיצות בכל אחד מהכיוונים, וצפרדע רשאית לקפוץ מעל הצבע שלה או מעל הצבע הנגדי, או מעל שני הצבעים. ארבע דוגמאות רצופות של קפיצות יבהירו הכל: `4` ל-`1, 5` ל-`4, 3` ל-`5, 6` ל-`3`. האם תוכלו להראות כיצד הן עושות זאת בעשרה קפיצות?

  • שאלה 217 - חידת טוויקנהאם

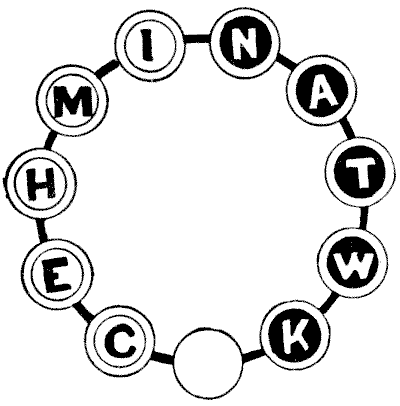    באיור יש לנו אחד עשר עיגולים במעגל. על חמישה מהעיגולים אנו מניחים חיילים לבנים עם אותיות שחורות - כפי שמוצג - ועל חמישה עיגולים אחרים חיילים שחורים עם אותיות לבנות. העיגול התחתון נותר ריק. כשהתחלנו כך, נדרש לסדר את החיילים כך שיאיית את המילה "Twickenham" בכיוון השעון, ולהשאיר את העיגול הריק במקומו המקורי. החיילים השחורים נעים בכיוון שמחוג השעון מסתובב, והחיילים הלבנים הולכים בכיוון ההפוך. חייל יכול לקפוץ מעל חייל בצבע הנגדי אם העיגול הריק נמצא מעבר לו. לכן, אם המהלך הראשון שלך הוא עם K, אז C יכול לקפוץ מעל K. אם אז K זז לכיוון E, אתה יכול לקפוץ W מעל C, וכן הלאה. ניתן לפתור את החידה בעשרים ושישה מהלכים. זכור, חייל לא יכול לקפוץ מעל חייל מצבעו שלו.

  • שאלה 218 - חידת צלב ויקטוריה

     

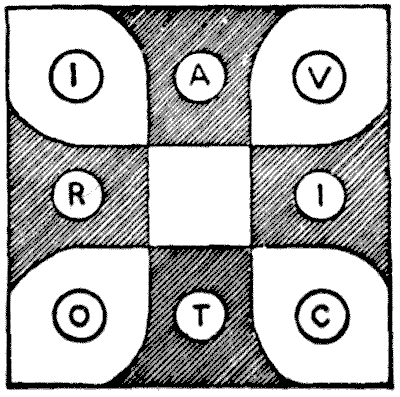
    יוצר החידות הוא באופן ייחודי "חוטף של דברים קטנים ולא חשובים," והיצירות שלו בנויות לעתים קרובות מחומרים דקים ביותר. טריוויאליות שיכולות לחמוק לחלוטין מתצפית של אחרים, או, אם היו נצפות, היו נחשבות כחסרות חשיבות אפשרית, מספקות לעתים קרובות את האדם שמחפש שאלות עם נושא יפה או רעיון שלדעתו יש לו ערך "בסיסי".

    כשישבתי מול גברת בקרון רכבת בתקופת יובל היהלום של המלכה ויקטוריה, תשומת ליבי נמשכה לסיכה שהיא ענדה. זה היה בצורה של צלב מלטזי או צלב ויקטוריה, ועליו האותיות של המילה ויקטוריה. המספר והסידור של האותיות נתנו לי מיד את ההצעה לחידה שאני מציג כעת.

    הדיאגרמה, כפי שניתן לראות, מורכבת מתשעה חלקים. החידה היא להניח שמונה אסימונים, הנושאים את האותיות של המילה ויקטוריה, בדיוק באופן המוצג, ואז להחליק אות אחת בכל פעם משחור ללבן ולבן לשחור לחלופין, עד שהמילה נקראת מסביב באותו כיוון, רק עם האות ההתחלתית V על אחת הזרועות השחורות של הצלב. בשום זמן לא יכולות להיות שתי אותיות באותו חלק. נדרש למצוא את השיטה הקצרה ביותר.

    מהלכי קפיצה אסורים, כמובן. המהלך הראשון חייב להיעשות בבירור עם A, I, T או R. נניח שאתה מעביר את T למרכז, האסימון הבא שישוחק יהיה O או C, מכיוון שאי אפשר להזיז את I או R. יש משהו קצת יוצא דופן בפתרון החידה הזו שאסביר.

  • שאלה 219 - פאזל קוביות האותיות

    הנה תזכורת קטנה לחברנו הוותיק, פאזל חמש-עשרה הבלוקים. שמונה קוביות עץ מסומנות באותיות, וממוקמות בקופסה, כפי שמוצג באיור. ניתן לראות שאפשר להזיז רק קובייה אחת בכל פעם למקום הפנוי באותו רגע, מכיוון שאף קובייה לא יכולה להיות מורמת מהקופסה. הפאזל הוא להזיז אותן עד שמקבלים אותן בסדר הזה— 

    A  B  C
    D  E  F
    G  H

    תגלו שזה לא קשה בכלל אם מותר לכם לבצע כמה מהלכים שתרצו. אבל הפאזל הוא לעשות את זה במספר המהלכים המועט ביותר האפשרי. אני לא אציין מה המספר הקטן ביותר הזה, כי ייתכן שהקורא ירצה לגלות זאת בעצמו. כשאתם רושמים את המהלכים שלכם, תגלו שאתם צריכים לרשום רק את האותיות בסדר שבו הן מוזזות. לדוגמה, חמשת המהלכים הראשונים שלכם עשויים להיות C, H, G, E, F; ולציון הזה לא יכולה להיות שום דו-משמעות. בפועל, אתם צריכים רק שמונה אסימונים ודיאגרמה פשוטה על דף נייר.

  • שאלה 220 - קושי בבית דירות

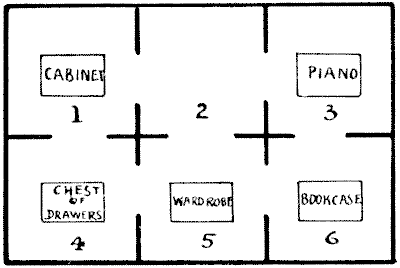    משפחת דובסון שכרה דירות בסלוקום-און-סי. היו שישה חדרים באותה קומה, כולם מחוברים, כפי שמוצג בתרשים. החדרים שהם לקחו היו מספרים `4, 5`, ו-`6`, כולם פונים לים. אבל התעוררה בעיה קטנה. מר דובסון התעקש שהפסנתר וארון הספרים יחליפו חדרים. זה היה ערמומי, כי משפחת דובסון לא הייתה מוזיקלית, אבל הם רצו למנוע מכל אחד אחר לנגן בכלי הנגינה. עכשיו, החדרים היו קטנים מאוד ופריטי הריהוט שצוינו היו גדולים מאוד, כך שלא ניתן היה להכניס שניים מהפריטים הללו לאף חדר באותו זמן. איך ניתן לבצע את ההחלפה עם מינימום עבודה? נניח, לדוגמה, שאתה מעביר תחילה את הארון לבגדים למספר `2`; אז אתה יכול להעביר את ארון הספרים למספר `5` ואת הפסנתר למספר `6`, וכן הלאה. זו חידה מרתקת, אבל לבעלת הבית היו סיבות לא להעריך אותה. נסה לפתור את הקושי שלה במספר המינימלי האפשרי של העברות עם אסימונים על דף נייר.