שעשועונים במתמטיקה, הנרי ארנסט דודני

• שאלה 261 - הנזיר והגשרים

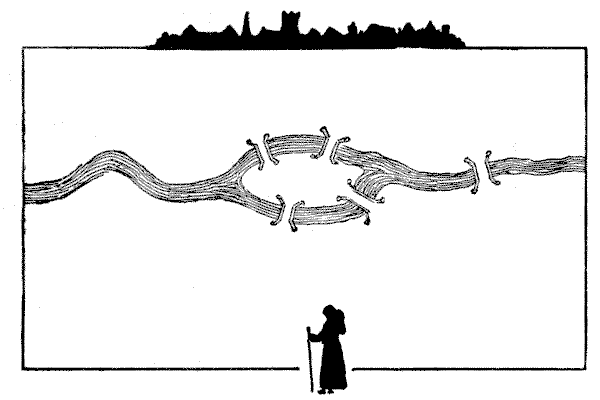
  במקרה הזה אני מציג תוכנית גסה של נהר עם אי וחמישה גשרים. בצד אחד של הנהר נמצא מנזר, ובצד השני נראה נזיר בחזית. כעת, הנזיר החליט שהוא יעבור כל גשר פעם אחת, ורק פעם אחת, בדרכו חזרה למנזר. זה כמובן די קל לעשות, אבל בדרך הוא חשב לעצמו, "אני תוהה כמה מסלולים שונים יש מהם יכולתי לבחור." האם הייתם יכולים לומר לו? זו החידה. קחו את העיפרון שלכם ועקבו אחר מסלול שייקח אתכם פעם אחת על פני כל חמשת הגשרים. לאחר מכן עקבו אחר מסלול שני, אחר כך שלישי, ובדקו אם אתם יכולים לספור את כל הווריאציות. תגלו שהקושי הוא כפול: עליכם להימנע מלהפיל מסלולים מצד אחד ולספור את אותם מסלולים יותר מפעם אחת מצד שני.

  נושאים:

  קומבינטוריקה -> תורת הגרפים

• שאלה 262 - חֲמֵשׁ עֶשְׂרֵה כְּבָשִׂים

  אנציקלופדיה מסוימת הציגה את הבעיה המוזרה הבאה, כך שמעתי: "הנח חמש עשרה כבשים בארבעה מכלאות כך שיהיה אותו מספר כבשים בכל מכלאה." לא ניתנה תשובה כלשהי, אז החלטתי לחקור את הנושא. ראיתי שבהתמודדות עם תפוחים או לבנים, הדבר ייראה בלתי אפשרי לחלוטין, מכיוון שארבע פעמים כל מספר חייב להיות מספר זוגי, בעוד שחמש עשרה הוא מספר אי-זוגי. לכן חשבתי שחייבת להיות תכונה מסוימת לכבשים שלא הייתה ידועה בדרך כלל. אז החלטתי לראיין כמה חקלאים בנושא. הראשון ציין שאם נכניס מכלאה אחת בתוך השנייה, כמו הטבעות של מטרה, ונניח את כל הכבשים במכלאה הקטנה ביותר, הכל יהיה בסדר. אבל התנגדתי לכך, כי אתה מודה שאתה מניח את כל הכבשים במכלאה אחת, לא בארבע מכלאות. האיש השני אמר שאם אני אניח ארבע כבשים בכל אחת משלוש מכלאות ושלוש כבשים במכלאה האחרונה (כלומר חמש עשרה כבשים בסך הכל), ולאחת הכבשות במכלאה האחרונה יהיה טלה במהלך הלילה, יהיה אותו מספר בכל מכלאה בבוקר. גם זה לא סיפק אותי. החקלאי השלישי אמר, "יש לי ארבע מכלאות גדר בשדה שלי, ועדר קטן של כבשים מסורסים, אז אם רק תרד איתי למטה אני אראה לך איך זה נעשה." האיור מתאר את ידידי כשהוא עומד להדגים לי את העניין. ההסבר הבהיר שלו היה כנראה זה שהיה במוחו של כותב המאמר באנציקלופדיה. מה זה היה? האם אתה יכול להניח את חמש עשרה הכבשים האלה?
  נושאים:

  אלגברה -> בעיות מילוליות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים

• שאלה 263 - אבירי המלך ארתור

  המלך ארתור ישב ליד השולחן העגול בשלושה ערבים רצופים עם אביריו - בלובוס, קרדוק, דריאם, אריק, פלול וגלהאד - אך בשום מקרה לא היה לאף אדם כשכן מישהו שישב לידו בעבר. בערב הראשון הם ישבו בסדר אלפביתי סביב השולחן. אבל אחר כך המלך ארתור סידר את שתי הישיבות הבאות כך שבלובוס יהיה קרוב אליו ככל האפשר וגלהאד רחוק ממנו ככל האפשר. איך הוא הושיב את האבירים בצורה הטובה ביותר, תוך שהוא זוכר את הכלל שאף אביר לא יכול לקבל את אותו שכן פעמיים?
  נושאים:

  קומבינטוריקה -> בדיקת מקרים -> תהליכים

• שאלה 264 - ארוחות הצהריים בעיר

  שנים עשר גברים הקשורים לחברה גדולה בעיר לונדון יושבים לארוחת צהריים יחד מדי יום באותו חדר. השולחנות קטנים ומספיקים רק לשני אנשים בו זמנית. האם תוכל להראות כיצד שנים עשר הגברים הללו יכולים לסעוד יחד במשך אחד עשר ימים בזוגות, כך שאף שניים מהם לא יישבו יחד פעמיים? אנו נייצג את הגברים באמצעות שתים עשרה האותיות הראשונות של האלף-בית, ונניח שההתאמה של היום הראשון היא כדלקמן—

  (A B) (C D) (E F) (G H) (I J) (K L).

  אז תן כל התאמה שתרצה ליום המחרת, למשל—

  (A C) (B D) (E G) (F H) (I K) (J L),

  וכן הלאה, עד שתשלים את אחד עשר השורות שלך, כך שאף זוג לא יופיע פעמיים. ישנם סידורים שונים רבים אפשריים. נסה למצוא אחד מהם.

  נושאים:

  קומבינטוריקה

• שאלה 265 - חידה לשחקני קלפים

  שנים עשר חברים במועדון תכננו לשחק ברידג' יחד באחד עשר ערבים, אך אף שחקן לא ישחק עם אותו שותף יותר מפעם אחת, או נגד אותו יריב יותר מפעמיים. האם תוכלו לתכנן תרשים המראה כיצד כולם יכולים לשבת בשלושה שולחנות בכל ערב? קראו לשנים עשר השחקנים על פי שתים עשרה האותיות הראשונות של האלף-בית ונסו לקבץ אותם.
  נושאים:

  קומבינטוריקה לוגיקה

• שאלה 266 - טורניר טניס

  ארבעה זוגות נשואים שיחקו טורניר טניס "זוגות מעורבים", גבר ואישה תמיד משחקים נגד גבר ואישה. אבל אף אדם לא שיחק עם או נגד אדם אחר יותר מפעם אחת. האם תוכלו להראות כיצד כולם יכלו לשחק יחד בשני מגרשים בשלושה ימים עוקבים? זוהי חידה קטנה מסוג מעשי למדי, והיא מבלבלת במידה מספקת כדי להיות מעניינת.
  נושאים:

  קומבינטוריקה -> עקרון שובך היונים קומבינטוריקה -> ספירה כפולה

• שאלה 267 - הכובעים הלא נכונים

  "אחד הדברים המבלבלים ביותר שנתקלתי בהם לאחרונה," אמר מר ווילסון, "הוא זה. שמונה גברים סעדו בחוכמה פחותה מדי במסעדה לונדונית מסוימת. הם היו האחרונים לעזוב, אך אף גבר לא היה במצב לזהות את הכובע שלו. עכשיו, בהתחשב בכך שהם לקחו את הכובעים שלהם באופן אקראי, מה הסיכויים שכל גבר לקח כובע שלא היה שייך לו?"

  "הדבר הראשון," אמר מר ווטרסון, "הוא לראות בכמה דרכים שונות ניתן לקחת את שמונת הכובעים."

  "זה די קל," הסביר מר סטאבס. "כפלו יחד את המספרים, `1, 2, 3, 4, 5, 6, 7`, ו-`8`. תן לי לראות—חצי דקה—כן; יש `40,320` דרכים שונות."

  "עכשיו כל מה שאתה צריך לעשות זה לראות בכמה מהמקרים האלה לאף אחד אין את הכובע שלו," אמר מר ווטרסון."

  תודה, אני לא לוקח כלום," אמר מר פקהרסט. "אני לא מקנא באיש שמנסה לבצע את המשימה של כתיבת כל ארבעים אלף המקרים המוזרים האלה ואז לבחור את אלה שהוא רוצה."

  כולם הסכימו שהחיים לא מספיק ארוכים בשביל סוג כזה של שעשוע; ומכיוון שאף אחד לא ראה דרך אחרת להגיע לתשובה, העניין נדחה לזמן בלתי מוגבל. האם אתה יכול לפתור את החידה?

  נושאים:

  קומבינטוריקה -> אינדוקציה קומבינטוריקה -> בדיקת מקרים -> תהליכים

• שאלה 268 - צלצול הפעמונים

  כתב לי קורספונדנט, שככל הנראה מתעניין מאוד בקמפנולוגיה, ושאל אותי איך עליו לבנות מה שהוא מכנה "צלצול אמיתי ונכון" עבור ארבעה פעמונים. הוא אומר שכל פרמוטציה אפשרית של ארבעת הפעמונים חייבת לצלצל פעם אחת, ופעם אחת בלבד. הוא מוסיף שאף פעמון לא חייב לזוז יותר ממקום אחד בכל פעם, שאף פעמון לא חייב להכות יותר משתי מכות רצופות במקום הראשון או האחרון, ושהשינוי האחרון חייב להיות מסוגל לעבור לראשון. ניתן לראות שתנאים פנטסטיים אלה נשמרים בצליל הקטן לשלושה פעמונים, כדלקמן:—

  1	2	3
  2	1	3
  2	3	1
  3	2	1
  3	1	2
  1	3	2

  כיצד עלינו לתת לו פתרון נכון לארבעת הפעמונים שלו?

  נושאים:

  קומבינטוריקה -> כלל המכפלה

• שאלה 269 - שלושה אנשים בסירה

  יצרן לונדוני נדיב מעניק מדי שנה לעובדיו שבוע חופשה על שפת הים על חשבונו. שנה אחת חמישה-עשר מעובדיו ביקרו בהרן ביי. בבוקר יציאתם מלונדון, פנה אליהם מעסיקם, שביטא את תקוותו שיבלו זמן נעים מאוד.

  "הבנתי," הוסיף, "שחלקכם אוהבים מאוד לשוט, ולכן אני מציע הפעם לספק לכם את הבילוי הזה, ובמקביל לתת לכם חידה משעשעת קטנה לפתור. במהלך שבעת הימים שבהם תשהו בהרן ביי, כל אחד מכם ייצא מדי יום בשעה קבועה לשייט, אך תמיד צריכים להיות שלושה אנשים בסירה ולא יותר. אסור לשני אנשים לצאת יחד בסירה יותר מפעם אחת, ואסור לאף אדם לצאת פעמיים באותה סירה. אם תצליחו לעשות זאת, ולהשתמש בכמה שפחות סירות שונות, תוכלו לחייב את החברה בהוצאות."

  אחד האנשים מספר לי שהניסיון שרכש בעניינים כאלה איפשר לו במהרה למצוא את הפתרון לשביעות רצונם המלאה ולשביעות רצונו של מעסיקם. אבל החלק המשעשע בעניין הוא שהם מעולם לא פתרו באמת את התעלומה הקטנה. אני מוצא שהשיטה שלהם הייתה שגויה לחלוטין, ואני חושב שזה ישעשע את קוראיי לגלות כיצד היה צריך להציב את האנשים בסירות. מכיוון ששמותיהם הם אנדרוז, בייקר, קרטר, דנבי, אדוארדס, פרית, גיי, הארט, אייזקס, ג'קסון, קנט, לאנג, מייסון, נאפר ואונסלו, נוכל לקרוא להם לפי ראשי התיבות שלהם ולכתוב את חמש הקבוצות לכל אחד משבעת הימים בצורה הפשוטה הבאה:

  	1	2	3	4	5
  יום ראשון:	(ABC)	(DEF)	(GHI)	(JKL)	(MNO).

  ניתן לראות כאן שהאנשים בתוך כל זוג סוגריים נמצאים באותה סירה, ולכן A לעולם לא יכול לצאת עם B או עם C שוב, ו-C לעולם לא יכול לצאת שוב עם B. אותו הדבר חל על ארבע הסירות האחרות. המספרים מראים את המספר על הסירה, כך ש-A, B או C, למשל, לעולם לא יכולים לצאת בסירה מס' `1` שוב.

  נושאים:

  קומבינטוריקה

• שאלה 270 - כדורי הזכוכית

  מספר קלעים פיקחים שהו שהו באחוזה כפרית, והמארח, כדי לספק קצת בידור, תלה שרשראות של כדורי זכוכית, כפי שמוצג באיור, כדי לירות עליהם. לאחר שכולם העמידו את כישוריהם למבחן מספיק, מישהו שאל את השאלה הבאה: "מהו המספר הכולל של דרכים שונות בהן ניתן לשבור את ששת-עשר הכדורים האלה, אם עלינו תמיד לשבור את הכדור הנמוך ביותר שנותר על כל חוט?" לדוגמה, דרך אחת תהיה לשבור את כל ארבעת הכדורים על כל חוט ברצף, תוך לקיחת החוטים משמאל לימין. דרך נוספת תהיה לשבור תחילה את כל הכדורים הרביעיים על ארבעת החוטים, ואז לשבור את שלושת הנותרים על החוט הראשון, ואז לקחת את הכדורים על שלושת החוטים האחרים לסירוגין מימין לשמאל, וכן הלאה. יש מספר עצום של דרכים שונות (מכיוון שכל וריאציה קטנה של סדר יוצרת דרך שונה) שאדם נוטה להתרשם בתחילה מהקושי הגדול של הבעיה. עם זאת, זה ממש פשוט ברגע שמצאת את השיטה הנכונה לתקוף אותה. כמה דרכים שונות יש?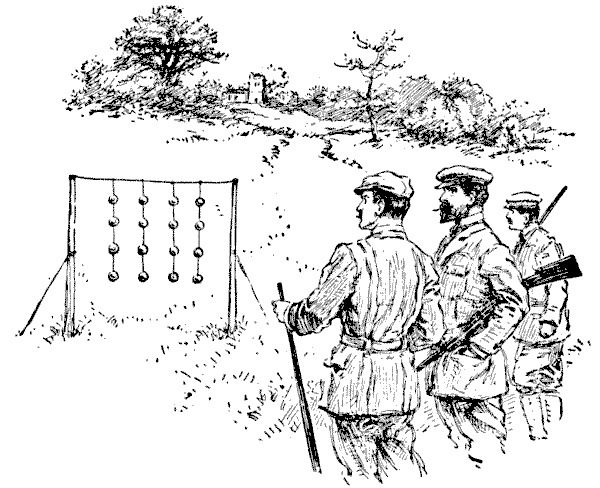
  נושאים:

  קומבינטוריקה -> כלל המכפלה