אלגברה, משוואות, משוואות דיופנטיות

משוואות דיופנטיות הן משוואות פולינומיאליות, בדרך כלל עם מקדמים שלמים, שעבורן מחפשים רק פתרונות שלמים. שאלות כוללות מציאת פתרונות שלמים אלו, קביעה האם קיימים פתרונות, או מציאת מספר הפתרונות (למשל, משוואות דיופנטיות לינאריות `ax+by=c`).

• חילוק סופי

  מצאו את כל ה x,y,z,w השלמים שמקיימים `x^2+y^2=3z^2+3w^2 `.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  תורת המספרים -> חשבון השאריות -> סימני חלוקה תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה אלגברה -> משוואות -> משוואות דיופנטיות

• חילוק סופי

  מצאו את כל ה x,y,z,w השלמים שמקיימים `x^2+y^2=3z^2+3w^2 `.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  תורת המספרים -> חשבון השאריות הוכחה ודוגמה -> הוכחה בשלילה אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות:
  • תרגילי הנבחרת הצעירה למדעים, 2024-2025, מטלה 1 שאלה 5

• שאלה

  מצאו את המספר `c` הקטן ביותר, כך שלמשוואה `3x + 4y = c` יהיו בדיוק 3 פתרונות במספרים שלמים חיוביים.

  נושאים:

  תורת המספרים אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות:
  • אולימפיאדת בנו ארבל, 2019, כיתה ז שאלה 5
  • אולימפיאדת בנו ארבל, 2019, כיתה ח שאלה 2

• שאלה

  מצא את כל הזוגות x ,y של מספרים שלמים, המקיימים את המשוואה `x + y = x^2 + xy + y^2`

  נושאים:

  אלגברה -> טכניקה אלגברית קומבינטוריקה -> בדיקת מקרים -> תהליכים אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשע"א, שלב א שאלה 8

• צוואה נדיבה

  אדם הותיר הוראות למנהלי העיזבון שלו לחלק פעם בשנה בדיוק חמישים וחמישה שילינגים לעניי הקהילה שלו; אבל הם היו אמורים להמשיך במתנה רק כל עוד הם יכולים לעשות זאת בדרכים שונות, תוך מתן שמונה עשר פני לכל אישה וחצי כתר לכל גבר. במשך כמה שנים אפשר היה לחלק את הצדקה? כמובן, ב"דרכים שונות" הכוונה היא למספר שונה של גברים ונשים בכל פעם.
  נושאים:

  אריתמטיקה אלגברה -> בעיות מילוליות אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 6

• קופסאות חג המולד

  לפני מספר שנים סיפר לי אדם שהוא השקיע מאה מטבעות כסף אנגליות בקופסאות חג המולד, כשנתן לכל אדם את אותו הסכום, וזה עלה לו בדיוק £`1, 10`s. `1`d. האם תוכלו לומר כמה אנשים קיבלו את המתנה, וכיצד הוא הצליח לחלק אותה? הפני המוזר הזה נראה מוזר, אבל הכל בסדר.
  נושאים:

  אריתמטיקה אלגברה -> בעיות מילוליות אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 23

• החידה של האב המנזר

  חידונאי האנגלי הראשון ששמו הגיע אלינו היה איש יורקשייר — לא אחר מאשר אלקווין, אב המנזר מקנטרברי (A.D. `735-804`). הנה חידה קטנה מכתביו, שלפחות מעניינת בשל עתיקותה. "אם `100` בושלים של תירס חולקו בין `100` אנשים באופן שכל גבר קיבל שלושה בושלים, כל אישה שניים, וכל ילד חצי בושל, כמה גברים, נשים וילדים היו שם?"

  כעת, ישנן שש תשובות נכונות שונות, אם נחריג מקרה שבו לא יהיו נשים. אבל נניח שהיו פי חמישה נשים מגברים, אז מה הפתרון הנכון?

  נושאים:

  אריתמטיקה אלגברה -> בעיות מילוליות אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 110

• המספר הקרוע

  

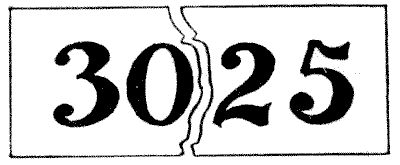
  היתה לי לאחרונה תווית ועליה המספר `3\ 0\ 2\ 5` בספרות גדולות. התווית הזו נקרעה בטעות לשניים, כך ש-`30` היה על חתיכה אחת ו-`25` על השנייה, כפי שמוצג באיור. כשבדקתי את החתיכות האלה התחלתי לעשות חישוב, כמעט בלי לשים לב מה אני עושה, ואז גיליתי את המוזרות הקטנה הזו. אם נחבר את ה-`30` ואת ה-`25` ונעלה את הסכום בריבוע, נקבל כתוצאה את המספר המקורי השלם שהיה על התווית! כלומר, `30` ועוד `25` זה `55`, ו-`55` כפול `55` זה `3025`. מוזר, לא? עכשיו, החידה היא למצוא מספר אחר, המורכב מארבע ספרות, שכולן שונות, שאותו ניתן לחלק באמצע ולקבל את אותה תוצאה.

  נושאים:

  תורת המספרים אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 113

• בעיה בריבועים

  יש ברשותנו שלושה לוחות מרובעים. שטח הפנים של הראשון מכיל חמישה רגל רבוע יותר מהשני, והשני מכיל חמישה רגל רבוע יותר מהשלישי. האם תוכלו לתת מידות מדויקות עבור צלעות הלוחות? אם תוכלו לפתור את החידה הקטנה הזו, נסו למצוא שלושה ריבועים בסדרה חשבונית, עם הפרש קבוע של `7` וגם של `13`.
  נושאים:

  תורת המספרים אלגברה -> סדרות -> סדרה חשבונית אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 128

• קרב הייסטינגס

  כל ההיסטוריונים יודעים שיש מידה רבה של מסתורין וחוסר ודאות בנוגע לפרטי הקרב הבלתי נשכח לעולם באותו יום גורלי, `14` באוקטובר `1066`. החידה שלי עוסקת בקטע מוזר בכרוניקה נזירית עתיקה שאולי לעולם לא תקבל את תשומת הלב הראויה לה, ואם אינני יכול לערוב לאותנטיות של המסמך, הוא בכל זאת ישמש אותנו כדי לספק לנו בעיה שקשה שלא תעניין את אותם קוראים שלי שיש להם נטיות אריתמטיות. הנה הקטע המדובר.

  "אנשיו של הרולד עמדו יחד היטב, כמנהגם, ויצרו שישים ואחת ריבועים, עם מספר שווה של אנשים בכל ריבוע מהם, ואוי לנורמני האמיץ שהעז להיכנס למעוזיהם; שכן מכה בודדת של גרזן מלחמה סקסוני תשבור את חניתו ותחתוך את מעיל השרשראות שלו.... כאשר הרולד השליך את עצמו לתוך המהומה, הסקסונים היו ריבוע אדיר אחד של אנשים, שצועקים את קריאות הקרב, 'Ut!' 'Olicrosse!' 'Godemitè!'"

  כעת, אני מגלה שכל הרשויות העכשוויות מסכימות שהסקסונים אכן נלחמו בסדר מוצק זה. לדוגמה, ב"Carmen de Bello Hastingensi," שיר המיוחס לגאי, הבישוף של אמיין, שחי בתקופת הקרב, נאמר לנו ש"הסקסונים עמדו קבועים במסה צפופה," והנרי מהנטינגדון רושם ש"הם היו כמו טירה, בלתי חדירים לנורמנים;" בעוד רוברט וייס, כעבור מאה שנה, מספר לנו את אותו הדבר. אז מבחינה זו הכרוניקה החדשה שלי עשויה שלא לטעות כל כך. אבל יש לי סיבה להאמין שמשהו לא בסדר עם המספרים בפועל. תן לקורא לראות מה הוא יכול לעשות מהם.

  מספר האנשים יהיה שישים ואחת פעמים מספר ריבועי; אבל כאשר הרולד עצמו הצטרף למהומה, הם הצליחו ליצור ריבוע גדול אחד. מהו המספר הקטן ביותר האפשרי של אנשים שיכולים היו להיות שם?

  כדי להבהיר לקורא את הפשטות של השאלה, אתן את הפתרונות הנמוכים ביותר במקרה של `60` ו-`62`, המספרים שמיד לפני ואחרי `61`. הם `60xx4^2+1 = 31^2`, ו-`62xx8^2+1=63^2`. כלומר, `60` ריבועים של `16` אנשים כל אחד יהיו `960` אנשים, וכאשר הרולד הצטרף אליהם הם יהיו `961` במספר, וכך יצרו ריבוע עם `31` אנשים בכל צד. באופן דומה במקרה של המספרים שנתתי עבור `62`. עכשיו, מצא את התשובה הנמוכה ביותר עבור `61`.

  נושאים:

  תורת המספרים אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 129