אולימפיאדת בנו ארבל, 2019, כיתה ח

• שאלה 1

  בשורה רשומים שישה מספרים טבעיים עוקבים בסדר עולה. האם ייתכן שסכום הספרות של המספר הראשון הוא 40 וגם שסכום הספרות של המספר האחרון הוא 18?

  נושאים:

  תורת המספרים -> חשבון השאריות -> סימני חלוקה קומבינטוריקה -> בדיקת מקרים -> תהליכים

• שאלה 2

  מצאו את המספר `c` הקטן ביותר, כך שלמשוואה `3x + 4y = c` יהיו בדיוק 3 פתרונות במספרים שלמים חיוביים.

  נושאים:

  תורת המספרים אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות נוספים:
  • אולימפיאדת בנו ארבל, 2019, כיתה ז שאלה 5

• שאלה 3

  חלקו את הצורה שבציור ל-7 חלקים חופפים.
  

  נושאים:

  גאומטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה

• שאלה 4

  מה יותר גדול ופי כמה:
  `(1 + 2/3) (2 + 3/4) ... (998 + 999/1000)` או `(3 + 2/1) (4 + 3/2) ... (1000 + 999/998)`

  נושאים:

  אריתמטיקה אלגברה -> סדרות אלגברה -> טכניקה אלגברית -> סכומים טלסקופיים
  מקורות נוספים:
  • אולימפיאדת בנו ארבל, 2019, כיתה ז שאלה 6

• שאלה 5

  בציור מצויר טרפז, שעל כל בסיס שלו נבחרו 5 נקודות. חלק מהנקודות חוברו על ידי קטעים ישרים. הראו כי סכום השטחים הכחולים שווה לסכום השטחים הכתומים.
  

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים

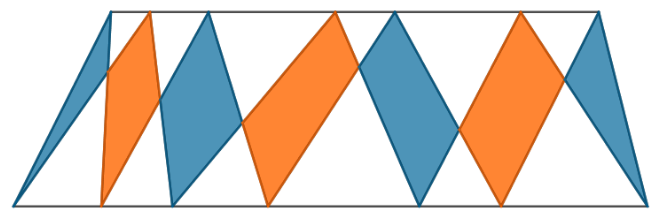
• שאלה 6

  על השולחן נמצאות 100 כוסות, ובהן `101, 102,...,200` חרצנים. שני אנשים משחקים במשחק הבא: כל אחד בתורו צריך לבחור כוס ולהוציא ממנה מספר כלשהו של חרצנים. אם לאחר מהלך של שחקן מסוים יימצאו שתי כוסות עם מספר זהה של חרצנים, הוא מפסיד. למי יש אסטרטגיית ניצחון: לשחקן הראשון או השני?

  נושאים:

  קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> תורת המשחקים
  מקורות נוספים:
  • אולימפיאדת בנו ארבל, 2019, כיתה ז שאלה 8

• שאלה 7

  החליפו אותיות בספרות שונות מאפס, כך שתתקבל זהות נכונה. אותיות זהות מסמנות ספרות זהות, אותיות שונות – ספרות שונות; גל, גר הם מספרים דו-ספרתיים שמורכבים מספרות אלו.
  `ל / ג + ל/ר + ל/ב + ל/(רג) + ל/ (ל ג) = ל`

  נושאים:

  תורת המספרים אלגברה -> משוואות אריתמטיקה -> שברים חידות ורבוסים -> שחזרו את התרגיל
  מקורות נוספים:
  • אולימפיאדת בנו ארבל, 2019, כיתה ט שאלה 6

• שאלה 8

  נתונים 5 מטבעות כסף זהים למראה, ו-5 מטבעות זהב זהים למראה. מבין מטבעות הכסף, יש ארבעה מטבעות אמיתיים והם זהים במשקל, ומטבע מזויף אחד שהוא כבד יותר ממטבע כסף אמיתי בגרם אחד. מבין מטבעות הזהב, יש ארבעה מטבעות אמיתיים והם זהים במשקל, ומטבע מזויף אחד שהוא קל יותר ממטבע זהב אמיתי בגרם אחד. האם אפשר למצוא את שני המטבעות המזויפים באמצעות 3 שקילות במאזני כף?

  נושאים:

  לוגיקה -> הגיון תורת האלגוריתמים -> שקילות קומבינטוריקה -> בדיקת מקרים -> תהליכים