קומבינטוריקה

קומבינטוריקה היא אמנות הספירה. היא עוסקת בבחירות, סידורים וצירופים של אובייקטים. שאלות כוללות קביעת מספר הדרכים לביצוע משימות, סידור פריטים (תמורות), או בחירת תת-קבוצות (צירופים), תוך שימוש לעיתים קרובות בעקרונות כמו עקרון המכפלה ועקרון הסכום.

עקרון שובך היונים ספירה כפולה מקדמים בינומיים ומשולש פסקל כלל המכפלה תורת הגרפים התאמות אינדוקציה תורת המשחקים גאומטריה קומבינטורית אינווריאנטים בדיקת מקרים תהליכים טבלאות מספריות צביעות

  • המלך והמבצרים

    היה היה, בעת העתיקה, מלך חזק, שהיו לו רעיונות מוזרים בנושא האדריכלות הצבאית. הוא טען שיש כוח וחיסכון גדולים בצורות סימטריות, ותמיד ציטט את דוגמת הדבורים, שבונות את החלות שלהן בתאים משושים מושלמים, כדי להוכיח שיש לו את הטבע שתומך בו. הוא החליט לבנות עשרה מבצרים חדשים במדינתו, שכולם יהיו מחוברים בחומות מבוצרות, שייצרו חמישה קווים עם ארבעה מבצרים בכל קו. האדריכל המלכותי הציג את תוכניתו המקדימה בצורה שהראיתי. אבל המלך הצביע על כך שניתן לגשת לכל מבצר מבחוץ, וציווה שהתוכנית תשונה כך שכמה שיותר מבצרים יהיו חופשיים מתקיפה מבחוץ, וניתן יהיה להגיע אליהם רק על ידי חציית החומות המבוצרות. האדריכל השיב שהוא חושב שאי אפשר לסדר אותם כך שאפילו מבצר אחד, שהמלך הציע להשתמש בו כמגורים מלכותיים, יהיה מוגן כל כך, אבל הוד מלכותו עד מהרה הבהיר לו כיצד ניתן לעשות זאת. איך הייתם בונים את עשרת המבצרים והביצורים כדי למלא בצורה הטובה ביותר את דרישות המלך? זכרו שהם חייבים ליצור חמישה קווים ישרים עם ארבעה מבצרים בכל קו.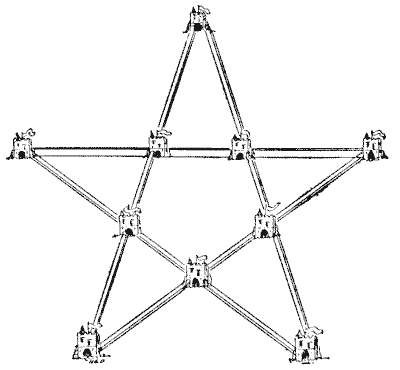 מקורות:

  • דובדבנים ושזיפים

    האיור הוא תוכנית של קוטג' כפי שהוא עומד מוקף במטע של חמישים וחמישה עצים. עשרה מהעצים הללו הם דובדבנים, עשרה הם שזיפים, והשאר תפוחים. הדובדבנים נשתלו כך שייצרו חמישה קווים ישרים, עם ארבעה עצי דובדבן בכל קו. עצי השזיף נשתלו גם הם כך שייצרו חמישה קווים ישרים עם ארבעה עצי שזיף בכל קו. החידה היא להראות אילו הם עשרת עצי הדובדבן ואילו הם עשרת עצי השזיף. על מנת שלדובדבנים ולשזיפים יהיה את הנוף הטוב ביותר, כמה שפחות (בתנאים הקיימים) נשתלים בצד הצפוני והמזרחי של המטע. כמובן שבהוצאת קבוצה של עשרה עצים (דובדבן או שזיף, לפי העניין) מתעלמים מכל העצים המפרידים. זאת אומרת, ארבעה עצים יכולים להיות בקו ישר ללא קשר לעצים אחרים (או לבית) שנמצאים ביניהם. אחרי החידה האחרונה זה יהיה די קל. מקורות:

  • חידת מטעים

    לאיש היתה חלקת אדמה מרובעת עם ארבעים ותשעה עצים, אך, כפי שניתן לראות מההשמטות באיור, ארבעה עצים נפלו וסולקו. כעת הוא רוצה לכרות את כל היתר מלבד עשרה עצים, שאותם יש להשאיר כך שהם ייצרו חמש שורות ישרות עם ארבעה עצים בכל שורה. אילו הם עשרת העצים שעליו להשאיר? מקורות:

  • עשרים ואחד עצים

    אדון רצה לשתול עשרים ואחד עצים בפארק שלו כך שהם ייצרו שתים עשרה שורות ישרות עם חמישה עצים בכל שורה. האם הייתם יכולים לספק לו סידור סימטרי נאה שיעמוד בתנאים אלה? מקורות:

  • עשרת המטבעות

    הניחו עשרה מטבעות פני על גיליון נייר או קרטון גדול, כפי שמוצג בתרשים, חמישה על כל קצה. כעת הסירו ארבעה מהמטבעות, מבלי להפריע לאחרים, והחזירו אותם לנייר כך שעשרת המטבעות ייצרו חמישה קווים ישרים עם ארבעה מטבעות בכל קו. זה כשלעצמו אינו קשה, אבל עליכם לנסות לגלות בכמה דרכים שונות ניתן לפתור את החידה, בהנחה שבכל מקרה שתי השורות בהתחלה זהות לחלוטין.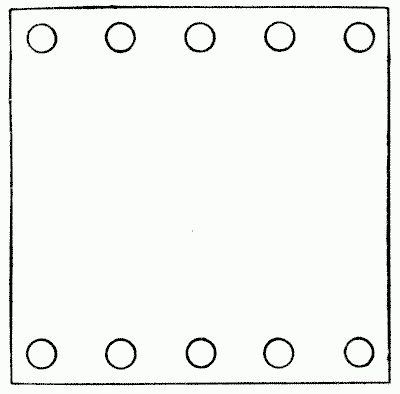 מקורות:

  • תריסר פשטידות בשר

    ניתן לראות באיור שלנו כיצד ניתן להניח תריסר פשטידות בשר על השולחן כך שייצרו שש שורות ישרות עם ארבע פשטידות בכל שורה. החידה היא להסיר רק ארבע מהן למיקומים חדשים כך שיהיו שבע שורות ישרות עם ארבע בכל שורה. אילו ארבע הייתם מסירים, והיכן הייתם מחליפים אותן?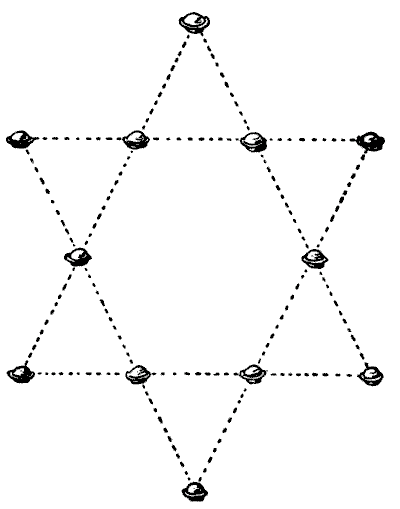 מקורות:

  • מטע בבורמה

    לפני זמן קצר קיבלתי מכתב מעניין מהכומר הבריטי במייקטילה, בורמה העליונה, בו כתב לי הכומר שנהנה באונייה בדרכו לשם לנסות לפתור את החידה הקטנה הזו.

     

    אם יש לו מטע של ארבעים ותשעה עצים, נטועים בצורת ריבוע כפי שמוצג באיור המצורף, הוא רוצה לדעת איך הוא יכול לכרות עשרים ושבעה מהעצים כך שעשרים ושניים העצים שיישארו יעמדו בשורות רבות ככל האפשר עם ארבעה עצים בכל שורה.

    כמובן שלא יכולים להיות יותר מארבעה עצים בשורה.

    מקורות:

  • טורקים ורוסים

    חידה זו היא בסגנון בעיית האפרידי שפורסמה על ידי ב-Tit-Bits לפני כמה שנים.

    על שטח מישורי פתוח, קבוצת חיילי רגלים רוסים, שאף אחד מהם לא הוצב באותו מקום, הופתעה לפתע על ידי שלושים ושניים טורקים, שפתחו באש על הרוסים מכל הכיוונים. כל אחד מהטורקים ירה בו זמנית כדור, וכל כדור חלף מיד מעל ראשיהם של שלושה חיילים רוסים. מכיוון שכל אחד מהכדורים הללו הרג אדם אחר, החידה היא לגלות מהו המספר הקטן ביותר האפשרי של חיילים שהקבוצה הרוסית יכולה הייתה להכיל ומה היו האבדות בכל צד.

    מקורות:

  • חידת החגב

    הועלתה סברה שהחידה הזו הייתה חביבה מאוד על החניכים הצעירים של הסיטי של לונדון במאות השש-עשרה והשבע-עשרה. הקוראים בוודאי הבחינו בחגב הפליז המוזר בבורסה המלכותית. יצור ארוך שנים זה ניצל משריפות `1666` ו-`1838`. החגב, כדרכו, היה סמל של סר תומס גרשם, סוחר מכולת, שמת בשנת `1579`, ומסיבה זו הוא שימש כסמל על ידי מכולת באופן כללי. למרבה הצער עבור האגדה לגבי מקורה, החידה הופקה על ידי עצמי רק בשנת `1900`. על שנים עשר מתוך שלושה עשר הדיסקים השחורים מונחים אסימונים ממוספרים או חגבים. החידה היא להפוך את סדרם, כך שיקראו, `1, 2, 3, 4` וכו', בכיוון ההפוך, כאשר הדיסק הריק נשאר באותו מיקום כמו עכשיו. הזיזו אחד בכל פעם בכל סדר, או לדיסק הריק הסמוך או על ידי קפיצה מעל חגב אחד, כמו המהלכים בדמקה. ניתן לבצע את המהלכים או הקפיצות בכל כיוון שאפשרי בכל עת. מהם מספר המהלכים המועט ביותר שבו ניתן לעשות זאת?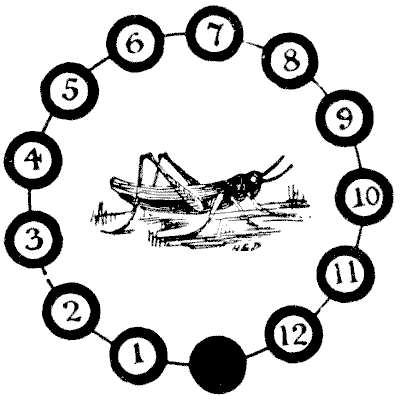 מקורות:

  • חידת מסילת רכבת

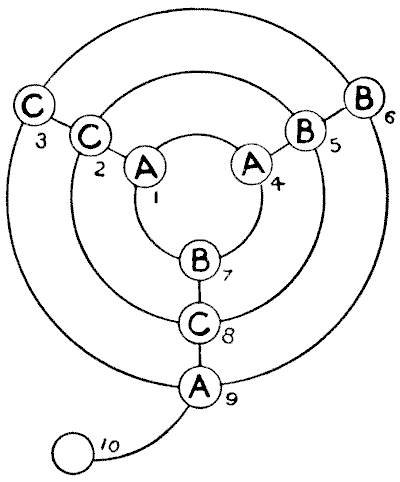    צרו דיאגרמה על דף נייר גדול, כמו באיור, והכינו שלושה אסימונים המסומנים ב-A, שלושה המסומנים ב-B ושלושה המסומנים ב-C. ניתן לראות שבצומת הקווים ישנם תשעה מקומות עצירה, ומקום עצירה עשירי מחובר למעגל החיצוני כמו הזנב של האות Q. הניחו את שלושת האסימונים או הקטרים המסומנים ב-A, את שלושת המסומנים ב-B ואת שלושת המסומנים ב-C במקומות המצוינים. החידה היא להזיז את הקטרים, אחד בכל פעם, לאורך הקווים, ממקום עצירה למקום עצירה, עד שתצליחו להשיג A, B ו-C על כל מעגל, וגם A, B ו-C על כל קו ישר. עליכם לעשות זאת בכמה שפחות מהלכים. כמה מהלכים אתם צריכים? מקורות: