קומבינטוריקה
קומבינטוריקה היא אמנות הספירה. היא עוסקת בבחירות, סידורים וצירופים של אובייקטים. שאלות כוללות קביעת מספר הדרכים לביצוע משימות, סידור פריטים (תמורות), או בחירת תת-קבוצות (צירופים), תוך שימוש לעיתים קרובות בעקרונות כמו עקרון המכפלה ועקרון הסכום.
עקרון שובך היונים ספירה כפולה מקדמים בינומיים ומשולש פסקל כלל המכפלה תורת הגרפים התאמות אינדוקציה תורת המשחקים גאומטריה קומבינטורית אינווריאנטים בדיקת מקרים תהליכים טבלאות מספריות צביעות-
חידת מוסך המכוניות
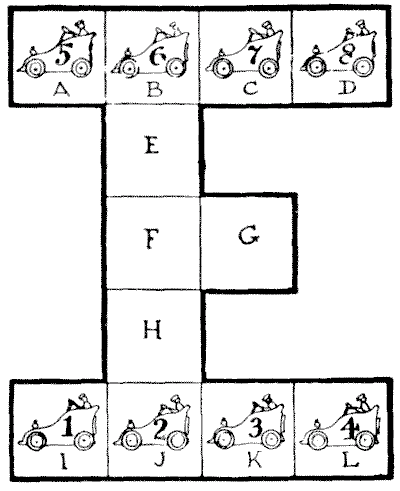
הקשיים של בעל מוסך מוסבים למעין בילוי שיש בו קסם מיוחד. כל מה שצריך זה להכין תוכנית או דיאגרמה פשוטה על דף נייר או קרטון ולמספר שמונה אסימונים, מ-`1` עד `8`. אז משפחה שלמה יכולה להיכנס לתחרות משעשעת כדי למצוא את הפתרון הטוב ביותר לקושי.
האיור מייצג את תוכנית מוסך המכוניות, עם מקום לשתים עשרה מכוניות. אבל השטח מצומצם בצורה לא נוחה, ולכן הבעלים נתקל לעתים קרובות במבוכה רבה. נניח, למשל, ששמונה המכוניות הממוספרות מ-`1` עד `8` נמצאות במקומות המוצגים, איך ניתן להזיז אותן בצורה המהירה ביותר כך ש-`1, 2, 3` ו-`4` יחליפו מקומות עם `5, 6, 7` ו-`8` — כלומר, כשהמספרים עדיין רצים משמאל לימין, כפי שהם כרגע, אבל השורה העליונה הוחלפה בשורה התחתונה? מהו המספר הקטן ביותר של מהלכים אפשריים?
מכונית אחת זזה בכל פעם, וכל מרחק נחשב למהלך אחד. כדי למנוע אי הבנות, מקומות העצירה מסומנים בריבועים, ויכולה להיות רק מכונית אחת בריבוע בכל פעם.
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 224
-
סוליטר מרכזי
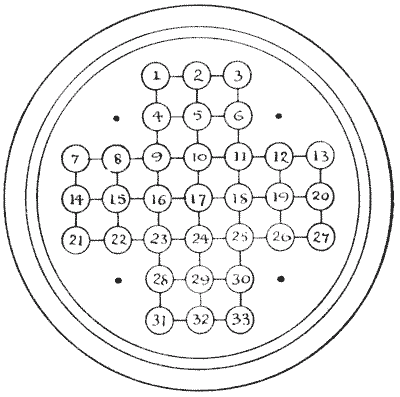
החידה העתיקה הזו הייתה חביבה מאוד על סבתותינו, ורובנו, אני מתאר לעצמי, נתקלנו מדי פעם בלוח "סוליטר" — לוח עגול מלוטש עם חורים החתוכים בו בדוגמה גיאומטרית, וגולה זכוכית בכל חור. לפעמים שמתי לב לאחד על שולחן צדדי בטרקלין קדמי פרברי, או שמצאתי אחד על מדף בקוטג' כפרי, או ששמו לב לאחד בפונדק דרכים. לפעמים הם מהצורה המוצגת לעיל, אך נפוץ באותה מידה שהלוח יהיו לו ארבעה חורים נוספים, בנקודות המסומנות בנקודות. אני בוחר בצורה הפשוטה יותר.
אף על פי שלוחי "סוליטר" עדיין נמכרים בחנויות הצעצועים, די יהיה אם הקורא יכין עותק מוגדל של הנ"ל על גיליון קרטון או נייר, ימספר את ה"חורים," ויספק לעצמו `33` אסימונים, כפתורים או שעועית. כעת הניחו אסימון בכל חור פרט למרכזי, מס' `17`, והחידה היא להסיר את כל האסימונים בסדרת קפיצות, למעט האסימון האחרון, שאותו יש להשאיר בחור המרכזי הזה. מותר לך לקפוץ אסימון אחד מעל האסימון הבא לחור פנוי מעבר לו, בדיוק כמו במשחק הדמקה, והאסימון שקפצו מעליו מוסר מיד מהלוח. רק זכור שכל מהלך חייב להיות קפיצה; כתוצאה מכך תסיר אסימון בכל מהלך, ושלושים ואחת קפיצות בודדות כמובן יסירו את כל שלושים ואחד האסימונים. אבל מותרים מהלכים מורכבים (כמו בדמקה, שוב), כל עוד אסימון אחד ממשיך לקפוץ, כל הקפיצות נחשבות למהלך אחד.
הנה ההתחלה של פתרון דמיוני שישמש כדי להבהיר לחלוטין את אופן התנועה, ולהראות כיצד הפותר צריך לכתוב את ניסיונותיו: `5-17`, `12-10`, `26-12`, `24-26` (`13-11`, `11-25`), `9-11` (`26-24`, `24-10`, `10-12`), וכו', וכו'. הקפיצות הכלולות בסוגריים נחשבות למהלך אחד, מכיוון שהן נעשות עם אותו אסימון. מצא את המספר המועט ביותר של מהלכים אפשריים. כמובן שאסורות קפיצות אלכסוניות; אתה יכול לקפוץ רק בכיוון הקווים.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 227
-
תשעת השקדים
"הנה חידה קטנה," אמר כומר, "שמצאתי אותה מרתקת במיוחד. היא כל כך פשוטה, ובכל זאת היא משאירה אותך מעוניין ללא הגבלת זמן."
הכומר הנכבד לקח דף נייר וחילק אותו לעשרים וחמישה ריבועים, כמו חלק מרובע של לוח שחמט. אחר כך הניח תשעה שקדים על הריבועים המרכזיים, כפי שמוצג באיור, שם ייצגנו דלפקים ממוספרים לנוחיות במתן הפתרון.
"עכשיו, החידה היא," המשיך הכומר, "להסיר שמונה מהשקדים ולהשאיר את התשיעי בריבוע המרכזי. אתה מבצע את ההסרות על ידי קפיצה של שקד אחד מעל שקד אחר לריבוע הריק שמעבר והסרת זה שקפצו מעליו—בדיוק כמו בדמקה, רק כאן אתה יכול לקפוץ לכל כיוון, ולא רק באלכסון. העניין הוא לעשות את זה במספר המהלכים המועט ביותר האפשרי."
ניסיון הדגמה הבא יבהיר הכל. קפוץ `4` מעל `1, 5` מעל `9, 3` מעל `6, 5` מעל `3, 7` מעל `5` ו-`2, 4` מעל `7, 8` מעל `4`. אבל `8` לא נשאר בריבוע המרכזי, כפי שהוא צריך להיות. זכור להסיר את אלה שאתה קופץ מעליהם. כל מספר של קפיצות ברציפות עם אותו שקד נחשב למהלך אחד.
מקורות: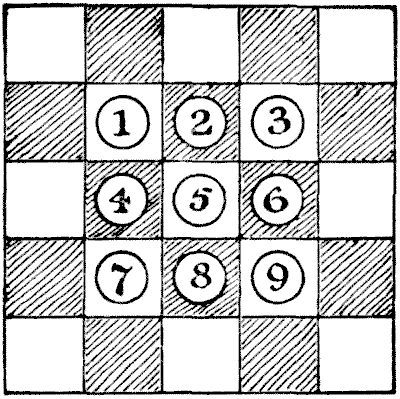
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 229
-
חידת ההחלפה
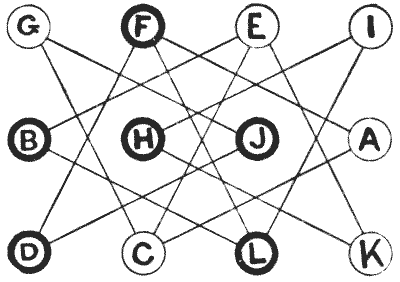
הנה חידה קטנה ומשעשעת עם העברת חיילים. אתה צריך רק שנים עשר חיילים—שישה מצבע אחד, המסומנים A, C, E, G, I ו-K, והשישה האחרים מסומנים B, D, F, H, J ו-L. אתה מניח אותם תחילה על הדיאגרמה, כפי שמוצג באיור, והחידה היא להביא אותם לסדר אלפביתי רגיל, כדלקמן:—
A B C D E F G H I J K L המהלכים מתבצעים על ידי החלפות של צבעים מנוגדים העומדים על אותו קו. כך, G ו-J יכולים להחליף מקומות, או F ו-A, אבל אינך יכול להחליף את G ו-C, או F ו-D, מכיוון שבמקרה אחד שניהם לבנים ובמקרה השני שניהם שחורים. האם אתה יכול להביא את הסידור הנדרש בשבע עשרה החלפות?
אי אפשר לעשות זאת בפחות מהלכים. החידה באמת הרבה יותר קלה ממה שהיא נראית, אם תוקפים אותה כראוי.
מקורות:נושאים:קומבינטוריקה -> אינווריאנטים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 234
-
אימון טורפדו
 אם צי של שישה עשר ספינות מלחמה עוגן ומוקף על ידי האויב, כמה ספינות עשויות לטבוע אם כל טורפדו, המשוגר בקו ישר, יעבור מתחת לשלוש ספינות ויטביע את הרביעית? בתרשים סידרנו את הצי במבנה ריבועי, שם ניתן לראות שאפשר להטביע עד שבע ספינות (אלו בשורה העליונה ובעמודה הראשונה) על ידי ירי הטורפדות המסומנים על ידי החצים. בעגינת הצי כרצוננו, עד כמה נוכל להגדיל את המספר הזה? זכרו שכל ספינה עוקבת טובעת לפני שיגור טורפדו נוסף, וכל טורפדו נע בכיוון אחר; אחרת, על ידי הצבת הספינות בקו ישר, אנו עשויים להטביע עד שלושה עשר! זהו מחקר קטן ומעניין בלוחמה ימית, ומעשי במיוחד - בתנאי שהאויב יאפשר לך לסדר את הצי שלו לנוחיותך ויבטיח לשכב בשקט ולא לעשות דבר!
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
אם צי של שישה עשר ספינות מלחמה עוגן ומוקף על ידי האויב, כמה ספינות עשויות לטבוע אם כל טורפדו, המשוגר בקו ישר, יעבור מתחת לשלוש ספינות ויטביע את הרביעית? בתרשים סידרנו את הצי במבנה ריבועי, שם ניתן לראות שאפשר להטביע עד שבע ספינות (אלו בשורה העליונה ובעמודה הראשונה) על ידי ירי הטורפדות המסומנים על ידי החצים. בעגינת הצי כרצוננו, עד כמה נוכל להגדיל את המספר הזה? זכרו שכל ספינה עוקבת טובעת לפני שיגור טורפדו נוסף, וכל טורפדו נע בכיוון אחר; אחרת, על ידי הצבת הספינות בקו ישר, אנו עשויים להטביע עד שלושה עשר! זהו מחקר קטן ומעניין בלוחמה ימית, ומעשי במיוחד - בתנאי שהאויב יאפשר לך לסדר את הצי שלו לנוחיותך ויבטיח לשכב בשקט ולא לעשות דבר!
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 235
-
סידור קופסאות הריבה
קרה שראיתי ילדה קטנה ממיינת ריבות בארון עבור אמה. היא הניחה כל סוג ריבה בנפרד על המדפים. שמתי לב שהיא לקחה צנצנת שזיפים ביד אחת וצנצנת דומדמניות ביד השנייה והחליפה ביניהן; אחר כך היא החליפה תות שדה עם פטל, וכן הלאה. היה מעניין לראות כמה טרחה מיותרת היא נתנה לעצמה על ידי ביצוע יותר החלפות ממה שהיה צורך, וחשבתי שזה יכול להפוך לחידה טובה.

כפי שניתן לראות באיור, דורותי הקטנה צריכה לתפעל עשרים וארבע קופסאות ריבה גדולות במספר תאים תואם. היא רוצה לסדר אותן בסדר מספרי נכון—כלומר, `1, 2, 3, 4, 5, 6` על המדף העליון, `7, 8, 9, 10, 11, 12` על המדף הבא, וכן הלאה. עכשיו, אם היא תמיד לוקחת קופסה אחת ביד ימין ואחת ביד שמאל ומחליפה ביניהן, כמה מההחלפות האלה יהיו נחוצות כדי לסדר את כל קופסאות הריבה בסדר הנכון? באופן טבעי היא תחליף קודם את `1` ואת `3`, אחר כך את `2` ואת `3`, ואז יהיו לה שלוש הקופסאות הראשונות במקומן. איך היית מייעץ לה להמשיך מכאן? הניחו כמה אסימונים ממוספרים על דף נייר המחולק למשבצות עבור התאים, ותגלו שזו חידה משעשעת.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 238
-
חידה לנוער
במשך שנים התייעצו איתי חבריי הצעירים ללא הרף לגבי החידה הקטנה הזו. נראה שרוב הילדים מכירים אותה, ובכל זאת, באופן מוזר למדי, הם תמיד לא מכירים את התשובה. השאלה שהם תמיד שואלים היא, "בבקשה, תגיד לי אם זה באמת אפשרי." אני מאמין שהודיני הקוסם נהג לחבב מאוד לתת אותה לחבריו הילדים, אבל אני לא יכול לומר אם הוא המציא את החידה הקטנה או לא. אין ספק שמספר גדול של קוראיי ישמחו לקבל את פתרון המסתורין, אז אני לא מתנצל על הצגת ה"טיזר" הישן הזה.
החידה היא לצייר בשלוש משיכות עיפרון את הדיאגרמה שהילדה הקטנה מציגה באיור. כמובן, אסור להרים את העיפרון מהנייר במהלך משיכה או לעבור על אותו קו פעם שנייה. תגלו שאתם יכולים להכניס חלק גדול מהדמות במשיכה רציפה אחת, אבל זה תמיד ייראה כאילו ארבע משיכות נחוצות.

צורה נוספת של החידה היא לצייר את הדיאגרמה על לוח ואז למחוק אותה בשלוש מחיקות.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 239
-
דגל היוניון ג'ק
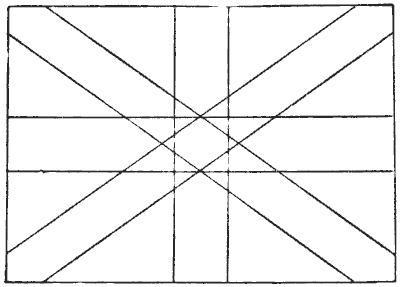 האיור הוא סקיצה גסה הדומה במידת מה לדגל הבריטי, היוניון ג'ק. לא ניתן לצייר את כולו מבלי להרים את העיפרון מהנייר או לעבור על אותו קו פעמיים. החידה היא לגלות בדיוק כמה מהציור אפשר לעשות מבלי להרים את העיפרון או לעבור פעמיים על אותו קו. קחו את העיפרון שלכם ובדקו מה הכי טוב שאתם יכולים לעשות.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
האיור הוא סקיצה גסה הדומה במידת מה לדגל הבריטי, היוניון ג'ק. לא ניתן לצייר את כולו מבלי להרים את העיפרון מהנייר או לעבור על אותו קו פעמיים. החידה היא לגלות בדיוק כמה מהציור אפשר לעשות מבלי להרים את העיפרון או לעבור פעמיים על אותו קו. קחו את העיפרון שלכם ובדקו מה הכי טוב שאתם יכולים לעשות.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 240
-
המעגל המנותח
כמה קווים רציפים, מבלי להרים את העיפרון מהנייר, נדרשים כדי לצייר את העיצוב המוצג באיור שלנו? ברגע שאתה משנה את כיוון העיפרון שלך, מתחיל קו חדש. אתה יכול לעבור על אותו קו יותר מפעם אחת אם תרצה. זה דורש קצת זהירות, או שאולי תגלה שהובסת על ידי קו אחד.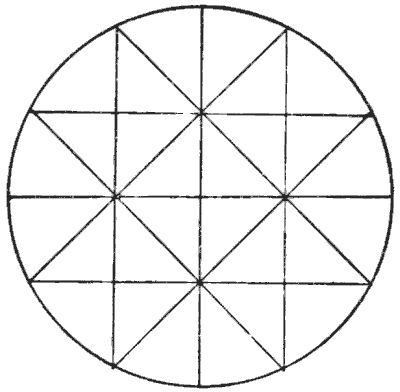 מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 241
-
החידה של מפקח הצינורות
האיש באיור שלנו נמצא בדילמה קטנה. הוא זה עתה מונה למפקח של מערכת מסוימת של רכבות תחתיות, וחובתו לבדוק באופן סדיר, בתוך תקופה מוגדרת, את כל שבעה-עשר הקווים של החברה המחברים שנים-עשר תחנות, כפי שמוצג בתוכנית הפוסטר הגדולה שהוא מהרהר בה. עכשיו הוא רוצה לארגן את המסלול שלו כך שהוא יעבור על כל הקווים עם כמה שפחות נסיעות. הוא יכול להתחיל איפה שהוא רוצה ולסיים איפה שהוא רוצה. מהו המסלול הקצר ביותר שלו?
האם יכול להיות משהו פשוט יותר? אבל הקורא יגלה עד מהרה, כי בכל דרך שיחליט להמשיך, המפקח חייב לעבור על חלק מהקווים יותר מפעם אחת. במילים אחרות, אם נאמר שהתחנות מרוחקות זו מזו במייל, הוא יצטרך לנסוע יותר משבעה-עשר מיילים כדי לבדוק כל קו. שם נמצא הקושי הקטן. כמה רחוק הוא נאלץ לנסוע, ואיזה מסלול אתה ממליץ?
 מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 242