קומבינטוריקה
קומבינטוריקה היא אמנות הספירה. היא עוסקת בבחירות, סידורים וצירופים של אובייקטים. שאלות כוללות קביעת מספר הדרכים לביצוע משימות, סידור פריטים (תמורות), או בחירת תת-קבוצות (צירופים), תוך שימוש לעיתים קרובות בעקרונות כמו עקרון המכפלה ועקרון הסכום.
עקרון שובך היונים ספירה כפולה מקדמים בינומיים ומשולש פסקל כלל המכפלה תורת הגרפים התאמות אינדוקציה תורת המשחקים גאומטריה קומבינטורית אינווריאנטים בדיקת מקרים תהליכים טבלאות מספריות צביעות-
טיול המכונית
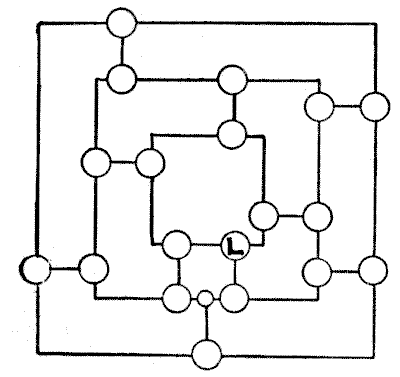 בתרשים לעיל, העיגולים מייצגים ערים והקווים מייצגים כבישים טובים. בכמה דרכים שונות בדיוק יכול נהג, היוצא מלונדון (מסומנת באות L), לערוך סיור בכל הערים הללו, לבקר בכל עיר פעם אחת בלבד בסיור, ולחזור תמיד ללונדון בנסיעה האחרונה? ההיפוך המדויק של כל מסלול אינו נחשב לשונה.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
בתרשים לעיל, העיגולים מייצגים ערים והקווים מייצגים כבישים טובים. בכמה דרכים שונות בדיוק יכול נהג, היוצא מלונדון (מסומנת באות L), לערוך סיור בכל הערים הללו, לבקר בכל עיר פעם אחת בלבד בסיור, ולחזור תמיד ללונדון בנסיעה האחרונה? ההיפוך המדויק של כל מסלול אינו נחשב לשונה.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 254
-
פאזל ה-LEVEL
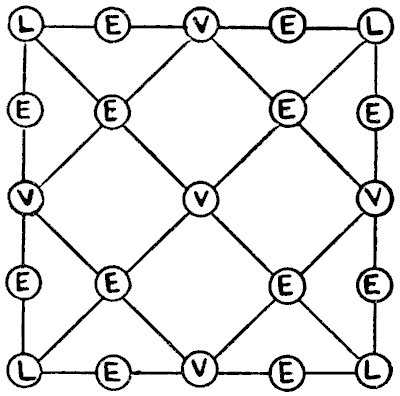 זהו פאזל ספירה פשוט. בכמה דרכים שונות ניתן לאיית את המילה LEVEL על ידי הנחת חוד העיפרון על L ולאחר מכן מעבר לאורך הקווים מאות לאות. מותר ללכת בכל כיוון, אחורה או קדימה. כמובן שאסור לפספס אותיות - כלומר, אם מגיעים לאות חייבים להשתמש בה.
מקורות:נושאים:קומבינטוריקה
זהו פאזל ספירה פשוט. בכמה דרכים שונות ניתן לאיית את המילה LEVEL על ידי הנחת חוד העיפרון על L ולאחר מכן מעבר לאורך הקווים מאות לאות. מותר ללכת בכל כיוון, אחורה או קדימה. כמובן שאסור לפספס אותיות - כלומר, אם מגיעים לאות חייבים להשתמש בה.
מקורות:נושאים:קומבינטוריקה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 255
-
חידת היהלום
בכמה דרכים שונות ניתן לקרוא את המילה DIAMOND (יהלום) בסידור המוצג? אפשר להתחיל היכן שרוצים באות D ולעלות או לרדת, אחורה או קדימה, פנימה והחוצה, בכל כיוון שרוצים, כל עוד עוברים תמיד מאות אחת לאחרת הצמודה לה. כמה דרכים יש?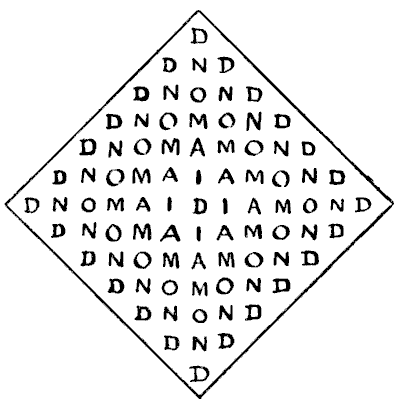 מקורות:נושאים:קומבינטוריקה
מקורות:נושאים:קומבינטוריקה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 256
-
החידה המאולצת
בכמה דרכים שונות ניתן לקרוא את המילה DEIFIED (מאוּלָה) בסידור הזה, באותם התנאים כמו בחידה האחרונה, בתוספת שאתה יכול להשתמש בכל אות פעמיים באותו קריאה?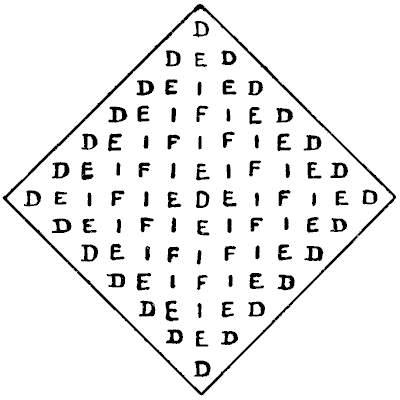 מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 257
-
חידת הבוחרים
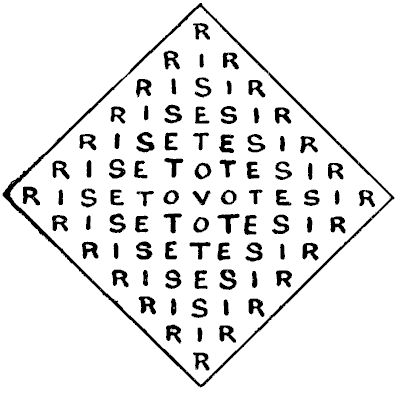 כאן יש לנו, אולי, את הצורה המעניינת ביותר של החידה. בכמה דרכים שונות ניתן לקרוא את הציווי הפוליטי, "RISE TO VOTE, SIR," תחת אותם תנאים כמו קודם? במקרה זה, כל קריאה של הפלינדרום מחייבת שימוש ב-V המרכזי כאות האמצעית.
מקורות:נושאים:קומבינטוריקה -> טבלאות מספריות
כאן יש לנו, אולי, את הצורה המעניינת ביותר של החידה. בכמה דרכים שונות ניתן לקרוא את הציווי הפוליטי, "RISE TO VOTE, SIR," תחת אותם תנאים כמו קודם? במקרה זה, כל קריאה של הפלינדרום מחייבת שימוש ב-V המרכזי כאות האמצעית.
מקורות:נושאים:קומבינטוריקה -> טבלאות מספריות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 258
-
החידה של חנה
איש היה מאוהב בגברת צעירה ששמה הפרטי היה חנה. כשביקש ממנה להיות אשתו היא כתבה את אותיות שמה באופן הזה:— והבטיחה שתהיה שלו אם יוכל לומר לה נכונה בכמה דרכים שונות אפשר לאיית את שמה, תמיד לעבור מאות אחת לאחרת שהיא סמוכה. צעדים אלכסוניים מותרים כאן. בין אם עשתה זאת רק כדי להקניט אותו או לבחון את חוכמתו לא נרשם, אבל משביע רצון לדעת שהוא הצליח. האם היית מצליח באותה מידה? קח את העיפרון שלך ונסה. אתה יכול להתחיל מכל אחת מהאותיות ה' וללכת אחורה או קדימה ובכל כיוון, כל עוד כל האותיות באיות סמוכות זו לזו. כמה דרכים יש, שאף שתיים מהן אינן זהות לחלוטין?
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
והבטיחה שתהיה שלו אם יוכל לומר לה נכונה בכמה דרכים שונות אפשר לאיית את שמה, תמיד לעבור מאות אחת לאחרת שהיא סמוכה. צעדים אלכסוניים מותרים כאן. בין אם עשתה זאת רק כדי להקניט אותו או לבחון את חוכמתו לא נרשם, אבל משביע רצון לדעת שהוא הצליח. האם היית מצליח באותה מידה? קח את העיפרון שלך ונסה. אתה יכול להתחיל מכל אחת מהאותיות ה' וללכת אחורה או קדימה ובכל כיוון, כל עוד כל האותיות באיות סמוכות זו לזו. כמה דרכים יש, שאף שתיים מהן אינן זהות לחלוטין?
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 259
-
הנזיר והגשרים
במקרה הזה אני מציג תוכנית גסה של נהר עם אי וחמישה גשרים. בצד אחד של הנהר נמצא מנזר, ובצד השני נראה נזיר בחזית. כעת, הנזיר החליט שהוא יעבור כל גשר פעם אחת, ורק פעם אחת, בדרכו חזרה למנזר. זה כמובן די קל לעשות, אבל בדרך הוא חשב לעצמו, "אני תוהה כמה מסלולים שונים יש מהם יכולתי לבחור." האם הייתם יכולים לומר לו? זו החידה. קחו את העיפרון שלכם ועקבו אחר מסלול שייקח אתכם פעם אחת על פני כל חמשת הגשרים. לאחר מכן עקבו אחר מסלול שני, אחר כך שלישי, ובדקו אם אתם יכולים לספור את כל הווריאציות. תגלו שהקושי הוא כפול: עליכם להימנע מלהפיל מסלולים מצד אחד ולספור את אותם מסלולים יותר מפעם אחת מצד שני.
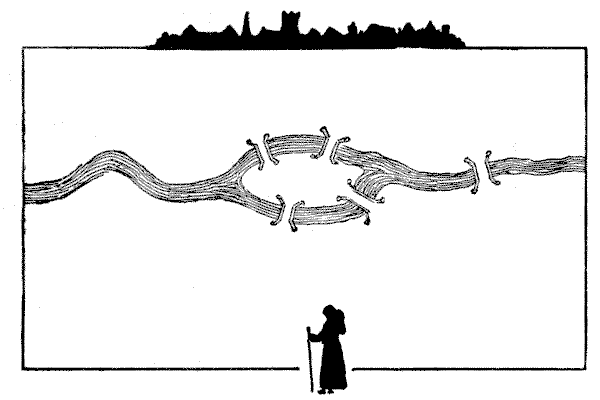 מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 261
-
חֲמֵשׁ עֶשְׂרֵה כְּבָשִׂים
אנציקלופדיה מסוימת הציגה את הבעיה המוזרה הבאה, כך שמעתי: "הנח חמש עשרה כבשים בארבעה מכלאות כך שיהיה אותו מספר כבשים בכל מכלאה." לא ניתנה תשובה כלשהי, אז החלטתי לחקור את הנושא. ראיתי שבהתמודדות עם תפוחים או לבנים, הדבר ייראה בלתי אפשרי לחלוטין, מכיוון שארבע פעמים כל מספר חייב להיות מספר זוגי, בעוד שחמש עשרה הוא מספר אי-זוגי. לכן חשבתי שחייבת להיות תכונה מסוימת לכבשים שלא הייתה ידועה בדרך כלל. אז החלטתי לראיין כמה חקלאים בנושא. הראשון ציין שאם נכניס מכלאה אחת בתוך השנייה, כמו הטבעות של מטרה, ונניח את כל הכבשים במכלאה הקטנה ביותר, הכל יהיה בסדר. אבל התנגדתי לכך, כי אתה מודה שאתה מניח את כל הכבשים במכלאה אחת, לא בארבע מכלאות. האיש השני אמר שאם אני אניח ארבע כבשים בכל אחת משלוש מכלאות ושלוש כבשים במכלאה האחרונה (כלומר חמש עשרה כבשים בסך הכל), ולאחת הכבשות במכלאה האחרונה יהיה טלה במהלך הלילה, יהיה אותו מספר בכל מכלאה בבוקר. גם זה לא סיפק אותי. החקלאי השלישי אמר, "יש לי ארבע מכלאות גדר בשדה שלי, ועדר קטן של כבשים מסורסים, אז אם רק תרד איתי למטה אני אראה לך איך זה נעשה." האיור מתאר את ידידי כשהוא עומד להדגים לי את העניין. ההסבר הבהיר שלו היה כנראה זה שהיה במוחו של כותב המאמר באנציקלופדיה. מה זה היה? האם אתה יכול להניח את חמש עשרה הכבשים האלה?
מקורות:נושאים:אלגברה -> בעיות מילוליות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים
החקלאי השלישי אמר, "יש לי ארבע מכלאות גדר בשדה שלי, ועדר קטן של כבשים מסורסים, אז אם רק תרד איתי למטה אני אראה לך איך זה נעשה." האיור מתאר את ידידי כשהוא עומד להדגים לי את העניין. ההסבר הבהיר שלו היה כנראה זה שהיה במוחו של כותב המאמר באנציקלופדיה. מה זה היה? האם אתה יכול להניח את חמש עשרה הכבשים האלה?
מקורות:נושאים:אלגברה -> בעיות מילוליות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 262
-
אבירי המלך ארתור
המלך ארתור ישב ליד השולחן העגול בשלושה ערבים רצופים עם אביריו - בלובוס, קרדוק, דריאם, אריק, פלול וגלהאד - אך בשום מקרה לא היה לאף אדם כשכן מישהו שישב לידו בעבר. בערב הראשון הם ישבו בסדר אלפביתי סביב השולחן. אבל אחר כך המלך ארתור סידר את שתי הישיבות הבאות כך שבלובוס יהיה קרוב אליו ככל האפשר וגלהאד רחוק ממנו ככל האפשר. איך הוא הושיב את האבירים בצורה הטובה ביותר, תוך שהוא זוכר את הכלל שאף אביר לא יכול לקבל את אותו שכן פעמיים?מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 263
-
ארוחות הצהריים בעיר
שנים עשר גברים הקשורים לחברה גדולה בעיר לונדון יושבים לארוחת צהריים יחד מדי יום באותו חדר. השולחנות קטנים ומספיקים רק לשני אנשים בו זמנית. האם תוכל להראות כיצד שנים עשר הגברים הללו יכולים לסעוד יחד במשך אחד עשר ימים בזוגות, כך שאף שניים מהם לא יישבו יחד פעמיים? אנו נייצג את הגברים באמצעות שתים עשרה האותיות הראשונות של האלף-בית, ונניח שההתאמה של היום הראשון היא כדלקמן—
(A B) (C D) (E F) (G H) (I J) (K L).
אז תן כל התאמה שתרצה ליום המחרת, למשל—
(A C) (B D) (E G) (F H) (I K) (J L),
וכן הלאה, עד שתשלים את אחד עשר השורות שלך, כך שאף זוג לא יופיע פעמיים. ישנם סידורים שונים רבים אפשריים. נסה למצוא אחד מהם.
מקורות:נושאים:קומבינטוריקה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 264