קומבינטוריקה, אינווריאנטים

אינווריאנט הוא תכונה של מערכת או אובייקט מתמטי הנשארת ללא שינוי כאשר מופעלות טרנספורמציות או פעולות. זיהוי אינווריאנט יכול להיות המפתח לפתרון בעיות על תהליכים או להוכחת אי-אפשרות. שאלות כוללות מציאת כמויות או תכונות קבועות כאלה.

• פומבה והסוכריות

  לפומבה יש 11 סוכריות שוקולד ו-13 סוכריות טופי. בכל פעם הוא יכול לאכול או שתי סוכריות מסוגים שונים,
  או שלוש סוכריות מאותו הסוג. מה הוא המספר הגדול ביותר של סוכריות שפומבה יוכל לאכול לפי הכללים האלה?

  נושאים:

  תורת המספרים -> חשבון השאריות -> סימני חלוקה קומבינטוריקה -> אינווריאנטים תורת המספרים -> חלוקה -> זוגיות קומבינטוריקה -> בדיקת מקרים -> תהליכים
  מקורות:
  • האולימפיאדה לצעירים, תשע"ח, גמר, כיתות ה-ו שאלה 6

• מעגל ושלוש נקודות

  על הלוח מצויר מעגל ועליו מסומנות שלוש נקודות בצבעים הבאים (לפי כיוון השעון): ירוק, כחול
  ואדום. יונתן משחק במשחק הבא – בכל שלב הוא יכול לעשות את אחד הצעדים הבאים:
  א) לבחור שתי נקודות סמוכות בעלות צבעים שונים ולצייר ביניהן נקודה באחד משני הצבעים האלו
  בלבד.
  ב) לבחור שתי נקודות סמוכות בעלות צבעים זהים ולצייר ביניהן נקודה בצבע כלשהו.
  ג) לבחור שלוש נקודות סמוכות שלפחות שתיים מהן באותו צבע, ולמחוק את האמצעית.

  האם יונתן יכול להגיע למצב שבו תיוותרנה על הלוח שלוש נקודות בצבעים הבאים (לפי כיוון השעון): כחול, ירוק, אדום? נמקו את תשובתכם

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> צביעות
  מקורות:
  • אולימפיאדת גיליס, תשע"ו שאלה 4

• לוח 2022x2022 ופעולות הפיכה

  יש לוח `2022 times 2022` עם מספרים ממשיים.

  בכל מהלך מותר לבחור שורה או עמודה ומספר ממשי `c`.

  אז מחליפים כל מספר בשורה או בעמודה מ `x` ל `c - x`.

  האם ניתן להגיע מכל לוח לכל לוח?

   

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  קומבינטוריקה -> אינווריאנטים אלגברה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> טבלאות מספריות

• שתי סולמיות

  מהו המספר המרבי של צורות "דומינו" (מלבנים `1 times 2` או `2 times 1`) שניתן למקם בתוך הצורה הכתומה,
  כך שהם לא יעלו אחד על השני ולא יחרגו מחוץ לגבולות הצורה?

  

  נושאים:

  קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> בדיקת מקרים -> תהליכים בעיות מינימום ומקסימום קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
  מקורות:
  • האולימפיאדה לצעירים, תש"פ, שלב ב, כיתות ג-ד שאלה 2
  • האולימפיאדה לצעירים, תש"פ, שלב ב, כיתות ה-ו שאלה 1

• שיוויון בשלבים

  על הלוח כתובים המספרים 1,2,3,4,5,6,7,8,9,10 ודוד אמור לשנות אותם בשלבים. בכל שלב מותר לדוד לבחור שני מספריים ולשנות אותם ב 1, כלומר להוסיף לשניהם 1, להחסיר משניהם 1, או להוסיף לאחד 1 ולהחסיר מהשני 1.

  האם דוד יוכל אחרי מספר שלבים להגיע למצב שבו כל המספרים על הלוח שווים? אם כן תראו דוגמא ואם לא נמקו את תשובתכם בפירוט.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  קומבינטוריקה -> אינווריאנטים לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות קומבינטוריקה -> בדיקת מקרים -> תהליכים
  מקורות:
  • תחרות גרוסמן, 2017, צעירים שאלה 3

• שאלה

  במעגל נמצאות 5778 נורות כבויות במרחקים קבועים. מתחת לכל נורה יש כפתור. כאשר לוחצים על הכפתור, זה משנה מצב של 4 נורות: הנורה שליד הכפתור, שתי נורות הבאות במעגל עם כיוון השעון, ואת הנורה הנגדית לכפתור (נורה כבויה נדלקת כאשר משנים את מצבה, ונורה דולקת נכבית). מהי הכמות המרבית של נורות שיכולות להיות דלוקות בו-זמנית?
  

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> אינווריאנטים לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> צביעות
  מקורות:
  • אולימפיאדת בנו ארבל, 2017, כיתה ח שאלה 8

• שאלה

  על השולחן נמצאות 100 כוסות, ובהן `101, 102,...,200` חרצנים. שני אנשים משחקים במשחק הבא: כל אחד בתורו צריך לבחור כוס ולהוציא ממנה מספר כלשהו של חרצנים. אם לאחר מהלך של שחקן מסוים יימצאו שתי כוסות עם מספר זהה של חרצנים, הוא מפסיד. למי יש אסטרטגיית ניצחון: לשחקן הראשון או השני?

  נושאים:

  קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> תורת המשחקים
  מקורות:
  • אולימפיאדת בנו ארבל, 2019, כיתה ז שאלה 8
  • אולימפיאדת בנו ארבל, 2019, כיתה ח שאלה 6

• חידת ההחלפה

  הנה חידה קטנה ומשעשעת עם העברת חיילים. אתה צריך רק שנים עשר חיילים—שישה מצבע אחד, המסומנים A, C, E, G, I ו-K, והשישה האחרים מסומנים B, D, F, H, J ו-L. אתה מניח אותם תחילה על הדיאגרמה, כפי שמוצג באיור, והחידה היא להביא אותם לסדר אלפביתי רגיל, כדלקמן:—

  A	B	C	D
  E	F	G	H
  I	J	K	L

  המהלכים מתבצעים על ידי החלפות של צבעים מנוגדים העומדים על אותו קו. כך, G ו-J יכולים להחליף מקומות, או F ו-A, אבל אינך יכול להחליף את G ו-C, או F ו-D, מכיוון שבמקרה אחד שניהם לבנים ובמקרה השני שניהם שחורים. האם אתה יכול להביא את הסידור הנדרש בשבע עשרה החלפות?

   

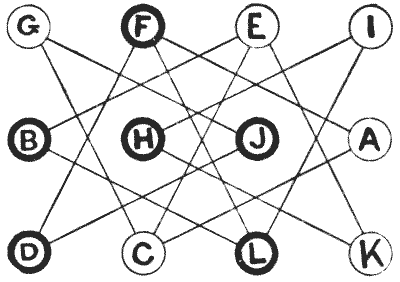
  אי אפשר לעשות זאת בפחות מהלכים. החידה באמת הרבה יותר קלה ממה שהיא נראית, אם תוקפים אותה כראוי.

  נושאים:

  קומבינטוריקה -> אינווריאנטים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 234

• שני הצריחים

  זוהי משחק חידה לשני שחקנים. לכל שחקן יש צריח אחד. השחקן הראשון מניח את הצריח שלו על כל משבצת בלוח שהוא בוחר, ואז השחקן השני עושה את אותו הדבר. עכשיו הם משחקים בתורות, כאשר המטרה של כל תור היא ללכוד את הצריח של היריב. אבל במשחק הזה אי אפשר לשחק דרך קו תקיפה מבלי להילכד. כלומר, אם בתרשים זה תורו של השחור לשחק, הוא לא יכול להזיז את הצריח שלו למשבצת של הפרש של המלך שלו, או למשבצת של הצריח של המלך שלו, כי הוא ייכנס ל"קו האש" כשהוא עובר על פני המשבצת של הרץ של המלך שלו. מאותה סיבה הוא לא יכול לעבור לצריח של המלכה שלו במשבצת השביעית או השמינית. עכשיו, המשחק לעולם לא יכול להסתיים בתיקו. במוקדם או במאוחר אחד הצריחים חייב ליפול, אלא אם כן, כמובן, שני השחקנים מבצעים את האבסורד של לא לנסות לנצח. הטריק לנצח הוא פשוט להפליא כשאתה יודע אותו. האם אתה יכול לפתור את החידה?
  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> תורת המשחקים לוגיקה -> הגיון קומבינטוריקה -> צביעות -> צביעת שחמט
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 393