גאומטריה, חשבון שטחים
נושא זה מתמקד בשיטות לקביעת גודלו של משטח או אזור דו-ממדי. שאלות כוללות חישוב שטחים של צורות גאומטריות שונות כמו משולשים, מרובעים, עיגולים וצורות מורכבות יותר, ולעיתים קרובות דורשות יישום של נוסחאות ספציפיות.
-
ריבוע הפורניר
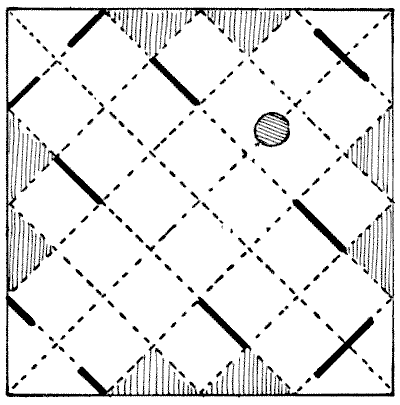
הבא מייצג חתיכת עץ ברשותי, `5` אינץ' מרובע. על ידי סימונים על פני השטח הוא מחולק לעשרים וחמישה אינצ'ים מרובעים. אני רוצה לגלות דרך לחתוך את חתיכת העץ הזו למספר המינימלי האפשרי של חלקים שיתאימו יחד וייצרו שני ריבועים מושלמים בגדלים שונים ובמידות ידועות. אבל, לצערי, בכל אחד משש עשרה הצמתים של קווי החיתוך נתקע מסמר קטן מתישהו, והמסור הנימי שלי ייפגע אם הוא יבוא במגע עם אחד מאלה. לכן אני צריך למצוא שיטה לעשות את העבודה שלא תחייב אותי לחתוך דרך אף אחת משש עשרה הנקודות האלה. איך זה אמור להיעשות? זכור, יש לתת את המידות המדויקות של שני הריבועים. מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 159
-
קופסת הנייר
אולי יהיה מעניין להציג כאן, למרות שזה לא בדיוק חידה, שיטה גאונית להכנת קופסת נייר.
קחו ריבוע של נייר עבה ובאמצעות קיפולים עוקבים צרו את כל הקמטים המסומנים על ידי הקווים המקווקווים באיור. לאחר מכן חתכו את שמונת החלקים המשולשים הקטנים המוצללים, וחתכו את הנייר לאורך הקווים הכהים. האיור השני מראה את הקופסה מקופלת למחצה, ולקורא לא תהיה בעיה להשלים את בנייתה. לפני הקיפול, הקורא יכול לגזור את החלק המעגלי המסומן בדיאגרמה, למטרה שאסביר כעת.
קופסה זו תשמש מצוין ליצירת טבעות מערבולת. טבעות אלה, שנדונו על ידי פון הלמהולץ ב-`1858`, מעניינות ביותר, והקופסה (עם החור החתוך) תיצור אותן בצורה מושלמת. מלאו את הקופסה בעשן טבק על ידי נשיפה עדינה דרך החור. כעת, אם תחזיקו אותה אופקית, ותקישו בעדינות על הצד הנגדי לחור, ניתן לייצר מספר עצום של טבעות מושלמות מפה אחת של עשן. עדיף שלא יהיו זרמי אוויר בחדר. אנשים לעתים קרובות לא מבינים שהטבעות האלה נוצרות באוויר כשלא משתמשים בעשן. העשן רק הופך אותן לגלויות. כעת, אחת מהטבעות האלה, אם היא מכוונת כראוי במסלולה, תנוע על פני החדר ותכבה את הלהבה של נר, והפעלול הזה מרשים הרבה יותר אם אתם מצליחים לעשות זאת בלי העשן. כמובן, עם קצת תרגול, ניתן לנשוף את הטבעות מהפה, אך הקופסה מייצרת אותן בשלמות רבה יותר, ואין צורך בשום מיומנות. לורד קלווין הציע את התיאוריה שהחומר עשוי להיות מורכב מטבעות מערבולת בנוזל הממלא את כל החלל, ועל ידי פיתוח ההשערה הוא הצליח להסביר צירופים כימיים.
מקורות: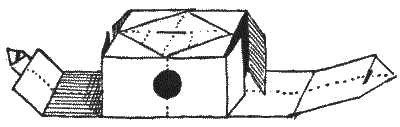
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 163
-
פרדוקס הטנגרם
תחביבים עתיקים רבים, כמו שחמט, התפתחו והשתנו במשך מאות שנים עד כדי כך שהממציאים המקוריים שלהם בקושי היו מזהים אותם. זה לא המקרה עם טנגרם, בילוי שנראה שהוא בן לפחות ארבעת אלפים שנה, שלכאורה מעולם לא היה רדום, ושלא שונה או "שופר" מאז שהסיני האגדי טאן חתך לראשונה את שבעת החלקים המוצגים בדיאגרמה I. אם תסמנו את הנקודה B, באמצע בין A ל-C, בצד אחד של ריבוע בכל גודל, ואת D, באמצע בין C ל-E, בצד סמוך, כיוון החיתוכים ברור מכדי להזדקק להסבר נוסף. כל עיצוב במאמר זה בנוי משבעת חלקי הקרטון המושחרים. מובן מיד שהשילובים האפשריים הם אינסופיים.
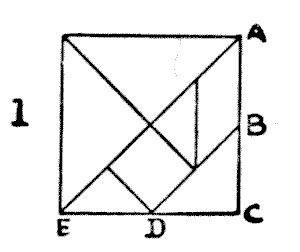
מר סם לויד המנוח, מניו יורק, שפרסם ספר קטן של עיצובים גאוניים מאוד, החזיק בכתבי היד של מר צ'אלנור המנוח, שערך מחקר ארוך ומעמיק על טנגרם. ג'נטלמן זה, כך אומרים, מתעד כי במקור היו שבעה ספרי טנגרם, שנערכו בסין אלפיים שנה לפני העידן הנוצרי. ספרים אלה נדירים כל כך, שאחרי ארבעים שנות מגורים בארץ, הוא הצליח לראות רק עותקים מושלמים של הכרכים הראשון והשביעי עם קטעים מהשני. חלקים מאחד הספרים, שהודפסו בעלי זהב על קלף, נמצאו בפקין על ידי חייל אנגלי ונמכרו בשלוש מאות לירות שטרלינג.
לפני כמה שנים הגיע לידי ספר קטן מהספרייה של לואיס קרול המנוח, שכותרתו The Fashionable Chinese Puzzle. הוא מכיל שלוש מאות עשרים ושלושה עיצובי טנגרם, בעיקר דמויות גיאומטריות חסרות ייחוד, שיש לבנות משבעת החלקים. הוא "פורסם על ידי ג'יי ואי. וואליס, `42` רחוב סקינר, וג'יי וואליס, ג'וניור, ספריית מרין, סידמות'" (דרום דבון). אין תאריך, אבל ההערה הבאה מציינת את זמן הפרסום די מקרוב: "המצאה גאונית זו הייתה במשך זמן מה הבילוי המועדף על הקיסר לשעבר נפוליאון, אשר, בהיותו כעת במצב מוחלש וחי מבודד מאוד, מבלה שעות רבות ביום באימון סבלנותו ותושייתו." הקורא יגלה, כפי שעשה הגולה הגדול, שאפשר להפיק הנאה רבה, לא לגמרי לא מלמדת, מיצירת עיצובים של אחרים. הוא ימצא שרבות מההמחשות למאמר זה קלות למדי לבנייה, וחלקן די קשות. כל תמונה יכולה להיחשב כחידה.
אבל זה בילוי אחר לגמרי ליצור עיצובים חדשים ומקוריים בעלי אופי ציורי, ומפתיע עד כמה הטנגרם מאפשר ליצור תמונות מחיי היומיום—זוויתיות ולעתים קרובות גרוטסקיות, זה נכון, אבל מלאות אופי. אני נותן דוגמה לדמות שוכבת (`2`) שהיא חיננית במיוחד, ורק צריכה הפחתה קלה של הזוויות שלה כדי לייצר מתאר משביע רצון לחלוטין.
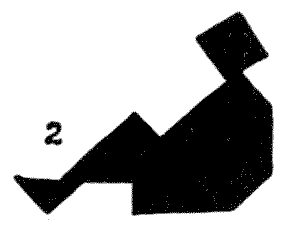
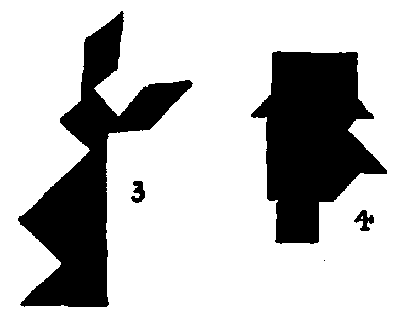
כפי שהתייחסתי למחבר Alice in Wonderland, אני נותן גם את העיצובים שלי של ארנבת מרץ (`3`) והכובען (`4`). אני נותן גם ניסיון לנפוליאון (`5`), ואינדיאני אדום מצוין מאוד עם הסקוו שלו על ידי מר לויד (`6` ו-`7`). מספר גדול של עיצובים אחרים ניתן למצוא במאמר שלי ב-The Strand Magazine לנובמבר, `1908`.

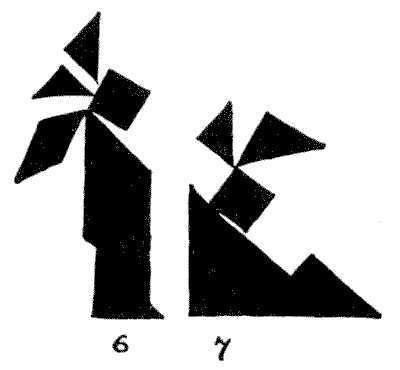
עם הופעתו של מאמר מגזין זה, סר ג'יימס מאריי המנוח, הפילולוג הדגול, ניסה, עם המסירות המדהימה שאפיינה את כל עבודתו, להתחקות אחר מקור המילה "טנגרם". לבסוף הוא כתב כדלקמן:—"אחד מבניי הוא פרופסור במכללה האנגלו-סינית בטיינטסין. דרכו, עמיתיו ותלמידיו, הצלחתי לברר לגבי הטן לכאורה בקרב חוקרים סינים. הפרופסור הסיני שלנו כאן (אוקספורד) גילה גם הוא עניין בעניין וקיבל מידע ממזכיר הנציגות הסינית בלונדון, שהוא נציג בולט מאוד של אנשי הספרות הסינים."
"התוצאה הייתה להראות שהאיש טאן, האל טאן ו'ספר הטאן' אינם ידועים כלל לספרות, להיסטוריה או למסורת הסינית. רוב האנשים המשכילים מעולם לא שמעו על השם, או הטענה על קיומם, של אלה. החידה, כמובן, ידועה היטב. היא נקראת בסינית ch'i ch'iao t'u; באופן מילולי, 'תוכנית שבע-מתוחכמת' או 'דמות חידה מתוחכמת של שבעה חלקים.' אף שם המתקרב ל'טנגרם', או אפילו 'טן', לא מופיע בסינית, וההצעות היחידות לאחרון היו ה-t'an הסיני, 'להרחיב'; או t'ang, ניב קנטונזי ל'סיני.' הוצע כי כנראה אמריקאי או אנגלי שידע קצת סינית או קנטונזית, שרצה שם לחידה, עשוי להמציא אחד מאחת המילים הללו והסיומת האירופית 'גרם.' אני הייתי אומר שהשם 'טנגרם' הומצא כנראה על ידי אמריקאי זמן קצר לפני `1864` ואחרי `1847`, אבל אני לא יכול למצוא אותו בדפוס לפני מהדורת `1864` של וובסטר. לכן נאלצתי להתייחס למילה בקצרה רבה במילון, ולספר למה היא מתייחסת ולאילו השערות או ניחושים נעשו לגבי השם, ונתתי כמה ציטוטים, אחד מהמאמר שלך עצמך, שאפשר לי לעשות יותר מהנושא ממה שיכולתי לעשות אחרת."
כמה כתבים הודיעו לי שהם מחזיקים, או החזיקו, דוגמאות של הספרים הסיניים הישנים. ג'נטלמן אמריקאי כותב לי כדלקמן:—"יש לי ספר עשוי נייר טישו, מודפס בשחור (עם כתובת סינית בעמוד הראשון), המכיל למעלה משלוש מאות עיצובים, השייך לקופסת 'טנגרם,' שבבעלותי גם כן. הבלוקים הם שבעה במספר, עשויים צדף, מלוטשים מאוד וחרוטים דק משני הצדדים. אלה כלולים בקופסת עץ ורד `2` `1/8` אינץ' מרובעת. דודי הגדול, ——, היה אחד המיסיונרים הראשונים שביקרו בסין. הקופסה והספר האלה, יחד עם אוסף של שרידים אחרים, נשלחו לסבי ועברו אלי."

הכתב שלי סיפק לי באדיבות שפשופים של הטנגרם, מהם ברור שהם חתוכים בפרופורציות המדויקות שאותן ציינתי. אני משחזר את הכתובת הסינית (`8`) מסיבה זו. הבעלים של הספר מודיע לי שהוא הגיש אותו למספר סינים בארצות הברית והציע דולר תמורת תרגום. אבל כולם סירבו בתוקף לקרוא את המילים, והציעו את התירוץ הצולע שהכתובת היא יפנית. ילידי יפן, לעומת זאת, מתעקשים שזה סיני. האם יש משהו נסתר ואזוטרי בטנגרם, שכל כך קשה להסיר את הצעיף? אולי דף זה יגיע לידיעת קורא כלשהו שמכיר את השפה הסינית, שיספק את התרגום הנדרש, שעשוי, או לא, להאיר מעט על שאלה מוזרה זו.

על ידי שימוש במספר סטים של טנגרם בו זמנית אנו עשויים לבנות תמונות שאפתניות יותר. חבר יעץ לי לא לשלוח את התמונה שלי, "משחק ביליארד" (`9`), לאקדמיה. הוא הבטיח לי שהיא לא תתקבל כי "השופטים כל כך כבולים על ידי מוסכמות." אולי הוא צדק, והיא תהיה מוערכת יותר על ידי פוסט-אימפרסיוניסטים וקוביסטים. השחקנים שוקלים מהלך עדין מאוד בראש השולחן. כמובן, שני האנשים, השולחן והשעון נוצרו מארבעה סטים של טנגרם. התמונה השנייה שלי נקראת "התזמורת" (`10`), והיא תוכננה לקישוט אולם מוזיקה גדול. כאן יש לנו את המנצח, הפסנתרן, נגן הקורנט השמנמן, הנגן השמאלי של הקונטרבס, שתנוחתו נאמנה למציאות, אם כי הוא עומד במרחק חריג מהכלי שלו, ואת ילד המתופף, עם מעמד התווים המרשים שלו. הכלב מאחורי הפסנתר אינו מיילל: הוא מאזין מעריך.


דבר אחד ראוי לציון בתמונות הטנגרם הללו הוא שהן מציעות לדמיון הרבה דברים שבאמת לא נמצאים שם. מי, למשל, יכול להסתכל כמה דקות על ליידי בלינדה (`11`) והנערה ההולנדית (`12`) מבלי להרגיש בקרוב את ההבעה היהירה במקרה אחד ואת המבט השובב במקרה השני? ואז הסתכלו שוב על החסידה (`13`), ותראו כיצד מוצע לתודעה שהרגל למעשה דקה בהרבה מכל אחד מהחלקים המשמשים. זו ממש אשליה אופטית. שוב, שימו לב במקרה של היאכטה (`14`) כיצד, על ידי השארת הנקודה הזוויתית הקטנה הזו בחלק העליון, מוצע תורן שלם. אם תשימו את הטנגרם שלכם יחד על נייר לבן כך שהם לא ממש נוגעים זה בזה, במקרים מסוימים האפקט משתפר על ידי הקווים הלבנים; במקרים אחרים זה כמעט נהרס.
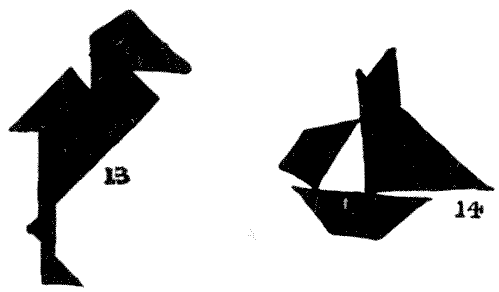
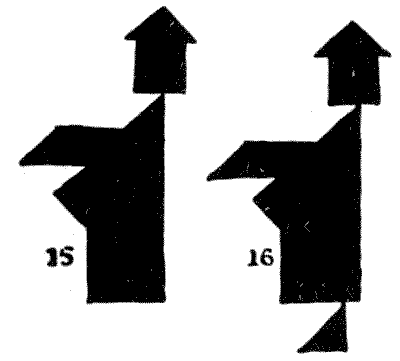
לבסוף, אני נותן דוגמה מהפרדוקסים המוזרים הרבים שאדם נתקל בהם בתפעול טנגרם. אני מראה עיצובים של שני אנשים מכובדים (`15` ו-`16`) שנראים בדיוק אותו הדבר, למעט העובדה שלאחד יש רגל ולשני אין. עכשיו, שתי הדמויות האלה עשויות מאותם שבעה טנגרם. מאיפה האיש השני מקבל את הרגל שלו?
 מקורות:נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
מקורות:נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 169
-
ריבועי הברוקד

קרה שנכחתי בביתה של גברת, כאשר הרמתי משולחן שני ריבועים יפהפיים של ברוקד. הם היו דוגמאות יפהפיות של אומנות מזרחית — שניהם באותו עיצוב, דוגמה משובצת עדינה
."הם לא מעודנים?" אמרה חברתי. "הם הובאו לי על ידי בן דוד שחזר זה עתה מהודו. עכשיו, אני רוצה שתעניק לי קצת עזרה. אתה רואה, החלטתי לחבר אותם יחד כדי ליצור כיסוי כרית מרובע גדול אחד. איך עלי לעשות זאת כדי לשחית את החומר כמה שפחות? כמובן שאני מציעה לבצע את החתכים שלי רק לאורך הקווים שמחלקים את המשבצות הקטנות."

חתכתי את שני הריבועים באופן הרצוי לארבעה חלקים שיכולים להתאים יחד וליצור ריבוע גדול יותר, תוך הקפדה על כך שהדוגמה תתאים כראוי, וכאשר סיימתי שמתי לב שלשניים מהחלקים יש בדיוק אותו שטח; כלומר, כל אחד משני החלקים הכיל את אותו מספר משבצות. האם אתה יכול להראות כיצד בוצעו החתכים בהתאם לתנאים אלה?
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 174
-
עוד חידת טלאים
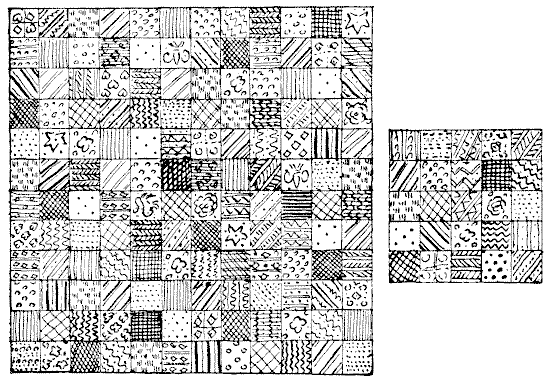 גברת קיבלה משתי חברותיה טלאי משי יפהפה, כפי שניתן לראות באיור. ניתן לראות ששני החלקים מורכבים מריבועים בגודל זהה - אחד `12x12` והשני `5x5`. היא מציעה לחבר אותם יחד וליצור שמיכת טלאים מרובעת אחת, `13x13`, אך כמובן, היא לא תחתוך אף אחד מהחומרים - רק תפרום את התפרים היכן שצריך ותחבר שוב. מה שמבלבל אותה הוא זה. חברה מבטיחה לה שלא צריך יותר מארבעה חלקים בסך הכל כדי לחבר לשמיכה החדשה. האם תוכלו להראות לה כיצד ניתן לפתור את חידת התפירה הקטנה הזו במספר כה מצומצם של חלקים?
מקורות:נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
גברת קיבלה משתי חברותיה טלאי משי יפהפה, כפי שניתן לראות באיור. ניתן לראות ששני החלקים מורכבים מריבועים בגודל זהה - אחד `12x12` והשני `5x5`. היא מציעה לחבר אותם יחד וליצור שמיכת טלאים מרובעת אחת, `13x13`, אך כמובן, היא לא תחתוך אף אחד מהחומרים - רק תפרום את התפרים היכן שצריך ותחבר שוב. מה שמבלבל אותה הוא זה. חברה מבטיחה לה שלא צריך יותר מארבעה חלקים בסך הכל כדי לחבר לשמיכה החדשה. האם תוכלו להראות לה כיצד ניתן לפתור את חידת התפירה הקטנה הזו במספר כה מצומצם של חלקים?
מקורות:נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 175
-
חיתוך לינולאום
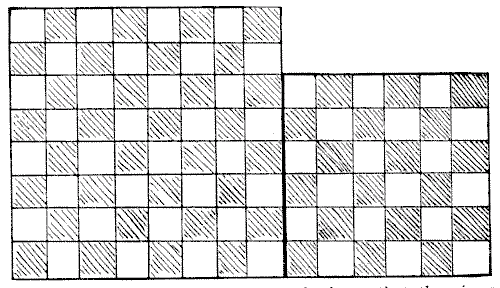 הדיאגרמה כאן מייצגת שני חלקי לינולאום נפרדים. דוגמת המשבצות לא חוזרת על עצמה בגב, כך שלא ניתן להפוך את החלקים. החידה היא לחתוך את שתי הריבועים לארבעה חלקים כך שהם יתאימו זה לזה וייצרו ריבוע מושלם אחד בגודל `10`×`10`, כך שהדוגמה תתאים כראוי, וכך שלחלק הגדול יותר יהיה חלק קטן ככל האפשר שנחתך ממנו.
מקורות:נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
הדיאגרמה כאן מייצגת שני חלקי לינולאום נפרדים. דוגמת המשבצות לא חוזרת על עצמה בגב, כך שלא ניתן להפוך את החלקים. החידה היא לחתוך את שתי הריבועים לארבעה חלקים כך שהם יתאימו זה לזה וייצרו ריבוע מושלם אחד בגודל `10`×`10`, כך שהדוגמה תתאים כראוי, וכך שלחלק הגדול יותר יהיה חלק קטן ככל האפשר שנחתך ממנו.
מקורות:נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 176
-
קופסת הקרטון
חידה זו אינה קשה, אך יהיה משעשע לגלות את הכלל הפשוט לפתרונה. יש לי קופסת קרטון מלבנית. לשטח החלק העליון `120` אינץ' רבוע, לשטח הצד `96` אינץ' רבוע, ולשטח הקצה `80` אינץ' רבוע. מהם הממדים המדויקים של הקופסה?מקורות:נושאים:גאומטריה -> גאומטריה במרחב גאומטריה -> חשבון שטחים אלגברה -> משוואות אלגברה -> בעיות מילוליות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 178
-
ארבעת הבנים
קוראים יזהו את הדיאגרמה כחבר ותיק מימי נעוריהם. לאיש הייתה אחוזה בצורת ריבוע. הוא הוריש לאלמנתו את הרבע המוצל של האחוזה. את היתר היה צריך לחלק באופן שווה בין ארבעת בניו, כך שכל אחד יקבל קרקע באותו שטח בדיוק ובאותה צורה בדיוק. מוצג לנו איך זה נעשה. אבל המשך הסיפור אינו ידוע כל כך. במרכז האחוזה הייתה באר, המסומנת על ידי הנקודה הכהה, ובנימין, צ'ארלס ודוד התלוננו שהחלוקה אינה "הוגנת", מכיוון שלאAlfred הייתה גישה לבאר הזו, בעוד שהם לא יכלו להגיע אליה מבלי להסיג את גבולו של מישהו אחר. החידה היא להראות כיצד יש לחלק את האחוזה כך שלכל בן תהיה קרקע באותו צורה ובאותו שטח, ולכל אחד תהיה גישה לבאר מבלי לרדת מהשטח שלו.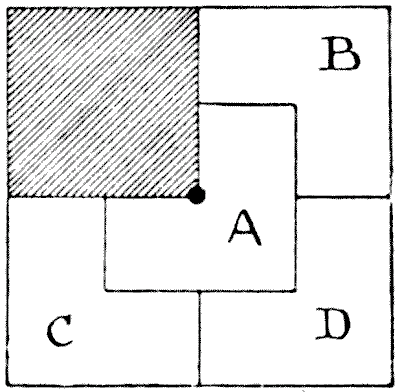 מקורות:נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
מקורות:נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 180
-
שלוש תחנות רכבת
כששבתי בקרון רכבת, הבחנתי בקצה השני של הקרון באדון מכובד, שהכרתי למראה, משוחח עם נוסע אחר, שהיה ככל הנראה חבר שלו.
"כמה רחוק אתה צריך לנסוע אל מקומך מתחנת הרכבת?" שאל הזר.
"ובכן," השיב האדון, "אם ארד באפלפורד, זה בדיוק אותו מרחק כמו אם אסע לברידג'פילד, עוד חמישה עשר מיילים הלאה; ואם אחליף רכבת באפלפורד ואסע משם שלושה עשר מיילים לקרטרטון, זה עדיין יהיה אותו מרחק. אתה רואה, אני נמצא במרחק שווה משלוש התחנות, אז יש לי מבחר טוב של רכבות."
ידעתי שבדיוק ברידג'פילד נמצאת במרחק של ארבעה עשר מיילים מקרטרטון, אז שעשעתי את עצמי בחישוב המרחק המדויק שהאדון צריך לנסוע הביתה, לא משנה באיזו תחנה הוא ירד. מה היה המרחק?
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 181
-
חידת הגינה
פרופסור רַאקְבְּרֵיין סיפר לי שעישן לאחרונה מקטרת ידידותית מתחת לעץ בגינה של מכר כפרי. הגינה הייתה מוקפת בארבעה קירות ישרים, וידידו הודיע לו שהוא מדד אותם ומצא שאורכם הוא `80, 45, 100`, ו-`63` יארד בהתאמה. "אם כך," אמר הפרופסור, "נוכל לחשב את השטח המדויק של הגינה." "זה בלתי אפשרי," השיב המארח שלו, "כי אתה יכול לקבל מספר אינסופי של צורות שונות עם ארבעת הצדדים האלה." "אבל אתה שוכח," אמר רַאקְבְּרֵיין, עם ניצוץ בעיניו, "שאמרת לי פעם ששתלת את העץ הזה במרחק שווה מכל ארבע פינות הגינה." האם תוכלו לחשב את שטח הגינה?מקורות:נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים אלגברה -> משוואות אלגברה -> בעיות מילוליות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 182