לוגיקה, הגיון
קטגוריה זו מדגישה כישורי חשיבה לוגית כלליים, המיושמים לעיתים קרובות בחידות או תרחישים שאינם פורמליים לחלוטין. היא כוללת דדוקציה, הסקה, זיהוי תבניות והסקת מסקנות מבוססות ממידע נתון. יש חפיפה עם לוגיקה פורמלית אך היא יכולה להיות רחבה יותר.
פרדוקסים-
קוביות האותיות - שלושים ושש
 האיור מייצג קופסה המכילה שלושים ושש קוביות אותיות. החידה היא לסדר מחדש את הקוביות כך שאף A לא יהיה בקו אנכי, אופקי או אלכסוני עם A אחר, אף B עם B אחר, אף C עם C אחר, וכן הלאה. תגלו שאי אפשר להכניס את כל האותיות לקופסה בתנאים אלה, אך העניין הוא למקם כמה שיותר. כמובן שאסור להשתמש באותיות אחרות מלבד אלה המוצגות.
מקורות:
האיור מייצג קופסה המכילה שלושים ושש קוביות אותיות. החידה היא לסדר מחדש את הקוביות כך שאף A לא יהיה בקו אנכי, אופקי או אלכסוני עם A אחר, אף B עם B אחר, אף C עם C אחר, וכן הלאה. תגלו שאי אפשר להכניס את כל האותיות לקופסה בתנאים אלה, אך העניין הוא למקם כמה שיותר. כמובן שאסור להשתמש באותיות אחרות מלבד אלה המוצגות.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 305
-
חידת מלכות ורץ
יובחן שכל משבצת בלוח היא תפוסה או מותקפת. החידה היא להחליף רץ בצריח באותה המשבצת, ואז להניח את ארבע המלכות על משבצות אחרות כך שכל משבצת שוב תהיה תפוסה או מותקפת.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 313
-
הצלב הדרומי

באיור לעיל יש לנו חמישה כוכבי לכת ושמונים ואחד כוכבים קבועים, כאשר חמישה מהאחרונים מוסתרים על ידי כוכבי הלכת. ניתן לראות שכל כוכב, למעט עשרת הכוכבים שיש להם נקודה שחורה במרכזם, נמצא בקו ישר, אנכית, אופקית או באלכסון, עם לפחות אחד מכוכבי הלכת. החידה היא לסדר מחדש את כוכבי הלכת כך שכל הכוכבים יהיו בקו אחד עם אחד או יותר מהם.
בסידור מחדש של כוכבי הלכת, כל אחד מחמשתם עשוי לנוע פעם אחת בקו ישר, בכל אחד משלושת הכיוונים שהוזכרו. הם, כמובן, יסתירו חמישה כוכבים אחרים במקום אלה המכוסים כעת.
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 314
-
שומרי האבירים
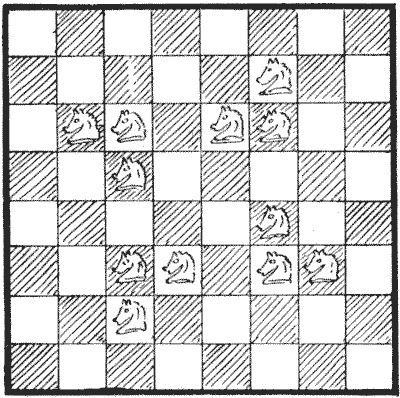
האביר הוא הקומיקאי הנמוך חסר האחריות של לוח השחמט. "הוא נוכל מאוד לא בטוח, מתגנב ומדכא," אומר סופר אמריקאי. "הוא יכול לזוז רק שני ריבועים, אך מפצה על כמות התנועה שלו באיכותה, שכן הוא יכול לקפוץ ריבוע אחד הצידה ואחד קדימה בו זמנית, כמו חתול; יכול לעמוד על רגל אחת באמצע הלוח ולקפוץ לכל אחד משמונת הריבועים שהוא בוחר; יכול לעלות על צד אחד של גדר ולהשמיץ שלושה או ארבעה אנשים בצד השני; יש לו דרך מעוררת התנגדות להכניס את עצמו למקומות בטוחים שבהם הוא יכול להפחיד את המלך ולאלץ אותו לזוז, ואז לטרוף מלכה. לרוע טהור אין לאביר שווה, וכאשר אתה רודף אחריו מחור אחד הוא קופץ לאחר." נעשו ניסיונות שוב ושוב להשיג הגדרה קצרה, פשוטה ומדויקת של תנועת האביר—ללא הצלחה. זה באמת מורכב מלהזיז ריבוע אחד כמו צריח, ואז ריבוע אחר כמו רץ—שני הפעולות נעשות בקפיצה אחת, כך שלא משנה אם הריבוע הראשון שעוברים עליו תפוס על ידי כלי אחר או לא. זו, למעשה, התנועה הקופצת היחידה בשחמט. אבל קשה ככל שיהיה להגדיר, ילד יכול ללמוד את זה על ידי הסתכלות תוך מספר דקות.
הראיתי בתרשים כיצד ניתן להציב שנים עשר אבירים (המספר הקטן ביותר האפשרי שיבצע את המשימה) על לוח השחמט כך שכל ריבוע יהיה או תפוס או מותקף על ידי אביר. בחן כל ריבוע בתורו, ותגלו שזה כך. כעת, החידה במקרה זה היא לגלות מהו המספר הקטן ביותר האפשרי של אבירים הנדרש כדי שכל ריבוע יהיה או תפוס או מותקף, וכל אביר מוגן על ידי אביר אחר. ואיך הייתם מסדרים אותם? יתברר שמתוך שנים עשר המוצגים בתרשים רק ארבעה מוגנים כך על ידי היותם במרחק מהלך של אביר מאביר אחר.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 319
-
מסע הצריח
אני קורא לחידה הזו "מסע הצריח", מכיוון שהמילה "tour" (הנגזרת מגלגל של חרט) מרמזת שאנו חוזרים לנקודה ממנה יצאנו, ואנו לא עושים זאת במקרה הזה. לא נהיה מרוצים מסיור חג מודרך אישית שהסתיים בכך שהשאיר אותנו, למשל, באמצע הסהרה. הצריח כאן עושה עשרים ואחד מהלכים, שבמהלכם הוא מבקר בכל משבצת בלוח פעם אחת בלבד, ועוצר במשבצת המסומנת `10` בסוף המהלך העשירי שלו, ומסתיים במשבצת המסומנת `21`. שני מהלכים רצופים אינם יכולים להתבצע באותו כיוון - כלומר, עליך לבצע פנייה לאחר כל מהלך.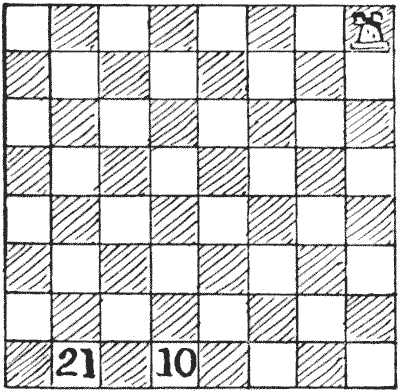 מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 321
-
החידה החדשה של הרץ

זוהי חידה קטנה ומסקרנת למדי. הניחו שמונה רצים (ארבעה שחורים וארבעה לבנים) על לוח השחמט המצומצם, כפי שמוצג באיור. הבעיה היא לגרום לרצים השחורים להחליף מקומות עם הלבנים, כך שאף רץ לא יתקוף רץ אחר מצבע מנוגד. הם חייבים לנוע לחלופין—תחילה רץ לבן, אחר כך רץ שחור, אחר כך רץ לבן, וכן הלאה. כאשר תצליחו לעשות זאת בכלל, נסו למצוא את מספר המהלכים המינימלי האפשרי.
אם תוציאו את הרצים שעומדים על משבצות שחורות, ותשחקו רק על המשבצות הלבנות, תגלו שהחידה האחרונה שלי הסתובבה על צידה.
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים קומבינטוריקה -> תורת המשחקים לוגיקה -> הגיון חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 327
-
פאזל הכוכבים

הניחו את חוד העיפרון שלכם על אחד הכוכבים הלבנים ו(מבלי להרים את העיפרון מהדף) מחקו את כל הכוכבים בארבעה עשר קווים ישרים רציפים, כשאתם מסיימים בכוכב הלבן השני. הקווים הישרים שלכם יכולים להיות בכל כיוון שתרצו, רק כל פנייה חייבת להתבצע על כוכב. אין התנגדות למחוק כוכב כלשהו יותר מפעם אחת.
במקרה הזה, כאשר ריבועי ההתחלה והסיום שלכם מקובעים בצורה לא נוחה, אינכם יכולים להשיג פתרון על ידי שבירת מסע מלכה, או בכל דרך אחרת באמצעות מסעי מלכה בלבד. אבל מותר לכם להשתמש בקווים ישרים אלכסוניים —כגון מהכוכב הלבן העליון ישירות לכוכב פינתי.
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 329
-
מבוי סתום
לפני מספר שנים הוצעה החידה לבנות משחק שחמט דמיוני, שבו הלבן יהיה במצב של מבוי סתום (stale mate) במספר המהלכים המועט ביותר האפשרי, כאשר כל שלושים ושניים הכלים נמצאים על הלוח. האם תוכלו לבנות מצב כזה בפחות מעשרים מהלכים? מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 349
-
דילמה מדהימה
במשחק שחמט בין מר בלק ומר וייט, בלק היה במצב קשה, וכרגיל נאלץ לתפוס רכבת. לכן הציע שווייט ישלים את המשחק בהיעדרו בתנאי שלא יבוצעו מהלכים כלשהם עבור בלק, אלא רק עם הכלים הלבנים. מר וייט הסכים, אך לתדהמתו גילה שאי אפשר לנצח במשחק בתנאים כאלה. ככל שניסה, לא הצליח לעשות שחמט ליריבו. באיזו משבצת השאיר מר בלק את המלך שלו? שאר הכלים נמצאים בעמדותיהם הנכונות בתרשים. וייט רשאי להשאיר את בלק בשח כמה פעמים שירצה, כי זה לא משנה, מכיוון שהוא לעולם לא יוכל להגיע לעמדת שחמט. מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 354
-
שַׁחְמָט מוּזָר
האם תוכל להניח שני צריחים לבנים ופרש לבן על הלוח כך שהמלך השחור (שחייב להיות באחד מארבעת הריבועים באמצע הלוח) יהיה בשח, ללא אפשרות תנועה פתוחה עבורו? "במילים אחרות," יאמר הקורא, "המלך יוצג כמט." ובכן, אתה יכול להשתמש במונח אם תרצה, אם כי אני בכוונה לא משתמש בו בעצמי. העובדה הפשוטה שאין מלך לבן על הלוח תהיה סיבה מספקת לכך שאני לא עושה זאת. מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 356