לוגיקה, הגיון

קטגוריה זו מדגישה כישורי חשיבה לוגית כלליים, המיושמים לעיתים קרובות בחידות או תרחישים שאינם פורמליים לחלוטין. היא כוללת דדוקציה, הסקה, זיהוי תבניות והסקת מסקנות מבוססות ממידע נתון. יש חפיפה עם לוגיקה פורמלית אך היא יכולה להיות רחבה יותר.

פרדוקסים

  • סיכת הָאֹדֶם

    בְּתוֹךְ דַּפֵּי יַעֲקוֹב סְקוֹטְלַנְד יַארְד נִמְצָאִים מִקְרֵי שׁוֹד תַּכְשִׁיטִים מְרַשְּׁמִים, אַךְ אֶחָד הַמְּסֻבָּכִים בְּיוֹתֵר הָיָה גְּנֵבַת הָאֲדָמִים שֶׁל לֵיְדִי לִיטֶלְוּוּד. הָיוּ, כַּמּוּבָן, גְּנֵבוֹת גְּדוֹלוֹת יוֹתֵר בְּמֻנָּחִים שֶׁל עֵרֶךְ, אַךְ מְעַטּוֹת הָיוּ מְפֻתָּלוֹת כָּל כָּךְ. לֵיְדִי לִיטֶלְוּוּד, מֵאֲחֻזַּת רוֹמְלִי, הָיְתָה יְרוּשָׁה יָפָה אַךְ קִיקְיוֹנִית מְעַט בְּצוּרַת סִיכַּת אֹדֶם. בְּעֵת שֶׁשָּׁהֲתָה בְּבֵיתָהּ שֶׁבָּעִיר בִּתְחִלַּת שְׁנוֹת הַשְּׁמוֹנִים הִיא לָקְחָה אֶת הַתַּכְשִׁיט לְחָנוּת בְּבְּרוֹמְפְּטוֹן לְתִקּוּנִים קַלִּים מְעַטִּים.

    "אֹסֶף מְעֻלֶּה שֶׁל אֲדָמִים, גְּבֶרֶת," אָמַר בַּעַל הַחֲנוּת, שֶׁלִּגְבִרְתָּהּ הָיָה זָר.

    "כֵּן," הֵשִׁיבָה; "אֲבָל דַּי לִפְלִיאָה כִּי לֹא סָפַרְתִּי אוֹתָם מַמָּשׁ אַף פַּעַם. אִמִּי הִצְבִּיעָה לְפָנַי פַּעַם שֶׁאִם מַתְחִילִים מֵהַמֶּרְכָּז וְסוֹפְרִים קַו אֶחָד לְמַעְלָה, לְאֹרֶךְ הַקָּצֶה וּלְמַטָּה בַּקַּו הַבָּא, תָּמִיד יֵשׁ שְׁמוֹנָה אֲדָמִים. כָּךְ תָּמִיד אֵדַע אִם חֲסֵרָה אֶבֶן.

     

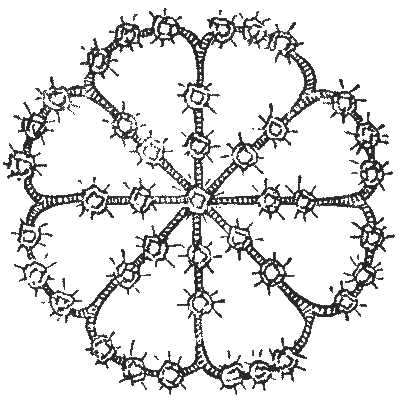
    שִׁשָּׁה חֳדָשִׁים לְאַחַר מִכֵּן אָח שֶׁל לֵיְדִי לִיטֶלְוּוּד, שֶׁחָזַר מֵהָרֶגִימֶנְט שֶׁלּוֹ בְּהוֹדּוּ, שָׂם לֵב שֶׁאֲחוֹתוֹ עוֹנֶדֶת אֶת סִיכַּת הָאֹדֶם בְּאֶחָד הַלֵּילוֹת בְּנֶשֶׁף מְחוֹזִי, וּבַחֲזָרָתָם הַבַּיְתָה בִּקֵּשׁ לְהִסְתַּכֵּל בָּהּ מִקָּרוֹב יוֹתֵר. מִיָּד גִּלָּה אֶת הָעֻבְדָּה שֶׁאַרְבַּע מֵהָאֲבָנִים נֶעֶלְמוּ.

    "אֵיךְ זֶה אֶפְשָׁר?" אָמְרָה לֵיְדִי לִיטֶלְוּוּד. "אִם סוֹפְרִים קַו אֶחָד מֵהַמֶּרְכָּז, לְאֹרֶךְ הַקָּצֶה, וּלְמַטָּה בַּקַּו הַבָּא, בְּכָל כִּוּוּן, תָּמִיד יֵשׁ שְׁמוֹנֶה אֲבָנִים. זֶה תָּמִיד הָיָה כָּךְ וְכָךְ זֶה עַכְשָׁו. אֵיךְ אֵפוֹא אֶפְשָׁר לְהָסִיר אֶבֶן בְּלִי שֶׁאֲגַלֶּה אוֹתָהּ?"

    "שׁוּם דָּבָר לֹא יָכוֹל לִהְיוֹת פָּשׁוּט יוֹתֵר," הֵשִׁיב הָאָח. "אֲנִי מַכִּיר אֶת הַסִּיכָּה הֵיטֵב. בְּמָקוֹר הִיא הִכִּילָה אַרְבָּעִים וְחָמֵשׁ אֲבָנִים, וְעַכְשָׁו יֵשׁ רַק אַרְבָּעִים וְאַחַת. מִישֶׁהוּ גָּנַב אַרְבָּעָה אֲדָמִים, וְאָז הִתְקִין מֵחָדָשׁ מִסְפָּר קָטָן כְּכָל הָאֶפְשָׁר שֶׁל הָאֲחֵרוֹת בְּצוּרָה שֶׁתָּמִיד יִהְיוּ שְׁמוֹנֶה בְּכָל אֶחָד מֵהַכִּוּוּנִים שֶׁצִּיַּנְתְּ."

    לֹא הָיָה סָפֵק קַל שֶׁצּוֹרֵף בְּרוֹמְפְּטוֹן הָיָה הַגַּנָּב, וְהָעִנְיָן הֻנַּח בִּידֵי הַמִּשְׁטָרָה. אֲבָל הָאִישׁ הָיָה דָּרוּשׁ לְגְנֵבוֹת אֲחֵרוֹת, וְעָזַב אֶת הַשְּׁכוּנָה כְּבָר לִפְנֵי זְמַן מָה. עַד הַיּוֹם הַזֶּה הוּא מֵעוֹלָם לֹא נִמְצָא.

    הַנְּקֻדָּה הַקְּטַנָּה הַמְּעַנְיֶנֶת שֶׁתְּחִלָּה תִּסְכְּלָה אֶת הַמִּשְׁטָרָה, וְשֶׁמְּעַצֶּבֶת אֶת נוֹשֵׂא הַחִידָה שֶׁלָּנוּ, הִיא זוֹ: אֵיךְ סֻדְּרוּ בְּמָקוֹר אַרְבָּעִים וְחָמֵשׁ הָאֲדָמִים עַל הַסִּיכָּה? הַתַּרְשִׁים מַרְאֶה בְּדִיּוּק אֵיךְ סֻדְּרוּ אַרְבָּעִים וְאַחַת לְאַחַר שֶׁחָזְרָה מֵאֵת הַצּוֹרֵף; אֲבָל אַף עַל פִּי שֶׁהֵם סוֹפְרִים שְׁמוֹנֶה נָכוֹן בְּכָל אֶחָד מֵהַכִּוּוּנִים הַמֻּזְכָּרִים, חֲסֵרוֹת אַרְבַּע אֲבָנִים.

    מקורות:

  • הגנן והטבחית

    כתב לי כתב שכינה את עצמו "סיימון הפשוט", והציע שאציג חידת תחבולה מיוחדת בגיליון של השבועון ליום השוטים הבינלאומי, `1900`. אז נתתי את החידה הבאה, והיא גרמה לשעשוע רב; מתוך קהל מתחרים גדול מאוד, רבים מהם מומחים למדי, אף אדם לא פתר אותה, למרות שהיא רצה כמעט חודש.

     

    "האיור הוא סקיצה דמיונית של הכתב שלי, 'סיימון הפשוט,' מנסה לפתור את החידה האריתמטית הקטנה והתמימה הבאה. מרוץ בין גבר לאישה שהייתי עד לו באחד מיום השוטים הבינלאומי נחקק בזיכרוני. זה קרה באחוזה כפרית, שם הגנן והטבחית החליטו לרוץ לתחרות לנקודה במרחק של `100` רגל ישר וחזרה. גיליתי שהגנן רץ `3` רגל בכל צעד והטבחית רק `2` רגל, אבל אז היא עשתה שלושה צעדים לשני הצעדים שלו. עכשיו, מה הייתה תוצאת המירוץ?"

    שבועיים לאחר הפרסום הוספתי את ההערה הבאה: "הועלתה ההצעה שאולי יש תחבולה ב'חזרה', אבל אין כזו. המירוץ הוא לנקודה במרחק `100` רגל וחזרה הביתה—כלומר, מרחק של `200` רגל. כתב אחד שואל האם לוקח להם בדיוק אותו זמן להסתובב, ואני משיב שכן. נראה שאחר חושד שזה בעצם חידה, והתשובה היא ש'תוצאת המירוץ הייתה תיקו (נישואין)'. אבל לא הייתה לי כוונה כזו. החידה היא אריתמטית, כפי שהיא מתיימרת להיות."

    מקורות:

  • מצא את אשת האיש

     

    יום אחד בקיץ בשנת `1903` הסתובבתי לאורך חזית ברייטון, צופה באנשים המטיילים על החוף, כאשר ידידי שליווה אותי משך לפתע את תשומת ליבי לאדם שעמד לבדו, ואמר, "האם תוכל להצביע על אשת האיש הזה? הם שוהים באותו מלון כמוני, והגברת היא אחת מאלה שנראות." לאחר מספר דקות של תצפית, הצלחתי לציין את הגברת בצורה נכונה. ידידי היה סקרן לדעת באיזו שיטת חשיבה הגעתי לתוצאה. זו הייתה תשובתי:—

    "אנו יכולים מיד להוציא מהכלל את אחות הרחמניות ואת הילדה בשמלה הקצרה; גם את האישה המוכרת תפוזים. זו לא יכולה להיות הגברת בבגדי אלמנות. זו לא הגברת בכיסא הגלגלים, כי היא לא שוהה במלון שלך, כי במקרה ראיתי אותה יוצאת מבית פרטי הבוקר בסיוע המשרתת שלה. שתי הנשים באדום סעדו ארוחת בוקר במלון שלי הבוקר, ומכיוון שלא לבשו בגדי חוץ, אני מסיק שהן שוהות שם. לכן זה נשען בין הגברת בכחול לזו עם השמשייה הירוקה. אבל היד השמאלית שמחזיקה את השמשייה היא, אתה רואה, לא מכוסה בכפפה ואין עליה טבעת נישואין. כתוצאה מכך, אני נאלץ למסקנה שהגברת בכחול היא אשת האיש הזה—ואתה אומר שזה נכון."

    כעת, מכיוון שידידי היה אמן, ומכיוון שחשבתי שאפשר להמציא חידה משעשעת על פי קווי השאלה שלו, ביקשתי ממנו להכין לי ציור לפי כמה הנחיות שנתתי לו, ויש לי תענוג להציג את התוצרת שלו לקוראים שלי. ניתן לראות שהתמונה מציגה שישה גברים ושש נשים: מס' `1, 3, 5, 7, 9` ו-`11` הן נשים, ומס' `2, 4, 6, 8, 10` ו-`12` הם גברים. שנים עשר האנשים האלה מייצגים שישה זוגות נשואים, שכולם זרים זה לזה, אשר, בהליכה חסרת מטרה, התערבבו. אבל אנחנו עוסקים רק באיש שחובש כובע קש—מספר `10`. החידה היא למצוא את אשת האיש הזה. בחנו את שש הנשים בקפידה, ובדקו אם תוכלו לקבוע מי מהן.

    הצגתי את התמונה באותה תקופה לכמה חברים, והם הביעו דעות שונות מאוד בנושא. אחד אמר, "אני לא מאמין שהוא יתחתן עם בחורה כמו מספר `7`." אחר אמר, "אני בטוח שבחורה נחמדה כמו מספר `3` לא תתחתן עם בחור כזה!" אחר אמר, "זה חייב להיות מספר `1`, כי היא התרחקה ככל האפשר מהבהמה!" הוצע שוב, שזה חייב להיות מספר `11`, כי "נראה שהוא מסתכל לעברה;" אבל ציניקן השיב, "בגלל אותה סיבה, אם הוא באמת מסתכל עליה, אני צריך לומר שהיא לא אשתו!"

    אני משאיר כעת את השאלה בידי הקוראים שלי. מי באמת אשתו של מספר `10`?

    האיור מצומצם בהכרח מאוד מהקנה מידה הגדול שבו הוא הופיע במקור בThe Weekly Dispatch (24 במאי `1903`), אך יש לקוות שהפרטים יהיו ברורים דיים כדי לאפשר לקורא להפיק בידור מבחינתו. בכל מקרה, הפתרון הניתן יאפשר לו לעקוב אחר הנקודות בעניין.


     

    מקורות:

  • שאלה

    יום אחד הארי פוטר מצא מחברת מוזרה בה היו כתובים מאה המשפטים הבאים:

    "במחברת הזאת יש בדיוק משפט אחד שהוא שקר"

    "במחברת הזאת יש בדיוק שני משפטים שהם שקר"

    "במחברת הזאת יש בדיוק שלושה שהם שקר "

    ...

    "במחברת הזאת יש בדיוק מאה משפטים שהם שקר "

    האם יש במחברת הזאת משפטים שהם אמת, ואם כן, אז כמה? נמקו!

  • הַנְס האמיץ והחוק האכזרי

    במדינה הקסומה חי אי פעם מלך אכזר. בסביבת הארמון שלו היה גשר, והוא העמיד על הגשר שומר שקיבל פקודות הבאות: הוא חייב לשאול את כל מי שעובר בגשר, למה הוא בא לפה. אם האיש עונה שקר, צריך לתלות אותו, ואם הוא עונה אמת – צריך לערוף לו את הראש.

    יום אחד הַנְס האמיץ היה צריך לעבור במקום הזה. כאשר השומר שאל אותו: "למה באת לפה?", הנס נתן תשובה כזאת שהשומר נאלץ לשחרר אותו. מה בדיוק הנס אמר לשומר?

  • הנס האמיץ והחוק האכזרי

    בארץ הקסומה חי אי פעם מלך אכזר. בסביבת הארמון שלו היה גשר, והוא העמיד על הגשר שומר שקיבל פקודות הבאות: הוא חייב לשאול את כל מי שעובר בגשר, למה הוא בא לפה. אם האיש עונה שקר, צריך לתלות אותו, ואם הוא עונה אמת – צריך לערוף לו את הראש.

    יום אחד הנס האמיץ היה צריך לעבור במקום הזה. כאשר השומר שאל אותו: "למה באת לפה?", הנס נתן תשובה כזאת שהשומר נאלץ לשחרר אותו. מה בדיוק הנס אמר לשומר?

  • שאלה

    כל האלופים אוכלים קורנפלקס של אלופים. שלומי אוכל קורנפלקס של אלופים. האם זה אומר שהוא אלוף?

  • שאלה

    חברה "הבונה החרוץ" עוסקת באגירת מלאי עצים ביער קסום בקנדה. עמותה להגנת הטבע בשם "הנוקם הירוק" רוצה להגן על היער ומתנגדת לפעילותה של החברה. בעקבות כך מנכ"ל החברה אמר את המשפט הבא:

    "`99%` של העצים ביער הם עצי מייפל. בשנה הקרובה אנו הולכים לכרות עצי מייפל בלבד, וכתוצאה מכך אחוז עצי מייפל ביער בעוד שנה יהפוך להיות `98%`. "

    איזה אחוז מעצי היער מתכוונים לכרות הבונים החרוצים?

  • מאיפה הופיע הטאלר המיותר?

    סנדלר בשם קרל תפר מגפיים ושלח את בנו הצעיר הַנְס לשוק כדי שהוא ימכור אותם בעבור `25` טאלר. בהגעתו של הנס לשוק, ניגשו אליו שני נכים, אחד בלי רגל שמאל, השני בלי רגל ימין, וביקשו למכור לכל אחד מהם מגף אחד. הנס הסכים ומכר לכל אחד מהם מגף ב-`12.5` טאלר.

    כשהנס חזר הביתה וסיפר לאבא מה קרה, קרל החליט שלאנשים האלה היה צריך למכור מגפיים במכיר נמוך יותר - `10` טאלר למגף. אז הוא נתן להנס `5` טאלר וביקש שיחזיר לכל אחד מהם `2.5` טאלר.

    בהגעתו לשוק הנס ראה דוחן ממתקים, לא התאפק ובזבז שם `3` טאלר ממה שהאבא נתן לו. אחרי זה הוא מצא את שני הנכים ונתן לכל אחד מהם טאלר אחד, כי זה כל מה שנשאר לו. כשהנס חזר הביתה, הוא התחרט על מה שהוא עשה וסיפר הכל לאבא. הסנדלר קרל התרגז מאוד ונעל את בנו במזוה בתור עונש.

    כך, יושב הנס במזוה ומנתח את מה שקרה באותו יום: "החזרתי לכל אחד מהנכים טאלר אחד, זה אומר שכל אחד מהם בסופו של דבר שילם על המגף שלו `12.5-1=11.5` טאלר. אז סך הכל הם שילמו `11.5*2=23` טאלר. ועוד שלושה טאלר בזבזתי על ממתקים. יוצא סך הכל  `26` טאלר, אבל היה `25`! מאיפה הופיע עוד טאלר אחד?"

     

  • שאלה

    מידי ערב יובל מסיים עבודה בזמן אקראי ומגיע לתחנת אוטובוס. בתחנה הזאת עוצרים שני אוטובוסים: מספר `7`, שנוסע לבית של יובל, ומספר `13`, שנוסע לבית של ידידו שלומי. יובל עולה על האוטובוס הראשון שמגיע וכתלות בכך נוסע לשלומי או הביתה.

    כעבור זמן מה יובל שם לב כי אחרי עבודה הוא נוסע לשלומי בערך פי שניים יותר מאשר הוא נוסע הביתה. הוא הסיק מזה שהאוטובוס מספר `13` מגיע בתדירות פי שניים גבוהה יותר מאוטובוס מספר `7`.

    האם יובל בהכרח צודק?