לוגיקה, הגיון

קטגוריה זו מדגישה כישורי חשיבה לוגית כלליים, המיושמים לעיתים קרובות בחידות או תרחישים שאינם פורמליים לחלוטין. היא כוללת דדוקציה, הסקה, זיהוי תבניות והסקת מסקנות מבוססות ממידע נתון. יש חפיפה עם לוגיקה פורמלית אך היא יכולה להיות רחבה יותר.

פרדוקסים

  • טריק עם קוביות

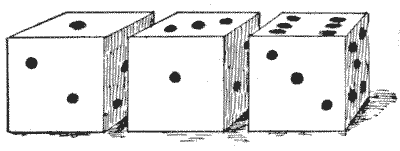    הנה טריק קטן ונחמד עם שלוש קוביות. אני מבקש ממך לזרוק את הקוביות מבלי שאראה אותן. לאחר מכן אני אומר לך להכפיל את הנקודות של הקוביה הראשונה ב-`2` ולהוסיף `5`; ואז להכפיל את התוצאה ב-`5` ולהוסיף את הנקודות של הקוביה השנייה; ואז להכפיל את התוצאה ב-`10` ולהוסיף את הנקודות של הקוביה השלישית. לאחר מכן אתה נותן לי את הסכום הכולל, ואני יכול מיד לומר לך את הנקודות שנזרקו בשלוש הקוביות. איך אני עושה את זה? לדוגמה, אם זרקת `1, 3`, ו-`6`, כפי שמוצג באיור, התוצאה שהיית נותן לי תהיה `386`, שממנה אוכל מיד לומר מה זרקת. מקורות:

  • משחק קריקט בכפר

    במשחק קריקט, Dingley Dell v. All Muggleton, האחרון קיבל את הסיבוב הראשון. מר דמפקינס ומר פודר היו בשערים, כאשר דמפקינס הזהיר ביצע חיתוך מאוחר מרהיב, ומר פודר קרא לו לרוץ. ארבע ריצות הושלמו לכאורה, אך השופטים הערניים בכל קצה קראו, "שלוש חסרות," מה שהפך לשש ריצות חסרות בסך הכל. איזה מספר השיג מר דמפקינס? כאשר Dingley Dell קיבלו את תורם בשערים, האלופים שלהם היו מר לאפי ומר סטראגלס. האחרון ביצע נסיעה מרהיבה מהצד, והזמין את עמיתו "לבוא," וכתוצאה מכך הצופים הבחינו ומחאו כפיים על מה שהיה אמור להיות שלוש ריצות חדות. אבל השופטים הצהירו שהיו שתי ריצות חסרות בכל קצה - ארבע בסך הכל. באיזו מידה, אם בכלל, התמרון הזה הגדיל את סך הנקודות של מר סטראגלס? מקורות:

  • שחקני הכדורגל

    "זהו משחק נפלא!" נשמע חובב נלהב קורא. "בסיום העונה שעברה, מבין שחקני הכדורגל שאני מכיר, לארבעה נשברה זרוע שמאל, לחמישה נשברה זרוע ימין, לשניים זרוע ימין הייתה בריאה, ולשלושה זרוע שמאל הייתה בריאה." האם תוכלו לגלות מההצהרה הזו מהו המספר הקטן ביותר של שחקנים שהדובר יכול היה להכיר?

    כלל לא נובע מכך שהיו ארבעה עשר אנשים, מכיוון שלדוגמה, שניים מהאנשים ששברו את זרוע שמאל יכולים להיות גם שניים מאלה שהייתה להם זרוע ימין בריאה.

    מקורות:

  • משחק החלוקים

    הנה משחק חידה קטן ומעניין שנהגתי לשחק עם מכר על החוף בסלוקומב-און-סי. שני שחקנים מניחים מספר אי זוגי של חלוקים, נניח חמישה עשר, ביניהם. לאחר מכן כל אחד בתורו לוקח אחד, שניים או שלושה חלוקים (כפי שהוא בוחר), והמנצח הוא זה שמקבל מספר אי זוגי. לכן, אם אתה מקבל שבע והיריב שלך שמונה, אתה מנצח. אם אתה מקבל שש והוא מקבל תשע, הוא מנצח. האם השחקן הראשון או השני אמור לנצח, וכיצד? לאחר שפתרתם את השאלה עם חמישה עשר חלוקים, נסו שוב עם, למשל, שלושה עשר. מקורות:

  • שני הצריחים

    זוהי משחק חידה לשני שחקנים. לכל שחקן יש צריח אחד. השחקן הראשון מניח את הצריח שלו על כל משבצת בלוח שהוא בוחר, ואז השחקן השני עושה את אותו הדבר. עכשיו הם משחקים בתורות, כאשר המטרה של כל תור היא ללכוד את הצריח של היריב. אבל במשחק הזה אי אפשר לשחק דרך קו תקיפה מבלי להילכד. כלומר, אם בתרשים זה תורו של השחור לשחק, הוא לא יכול להזיז את הצריח שלו למשבצת של הפרש של המלך שלו, או למשבצת של הצריח של המלך שלו, כי הוא ייכנס ל"קו האש" כשהוא עובר על פני המשבצת של הרץ של המלך שלו. מאותה סיבה הוא לא יכול לעבור לצריח של המלכה שלו במשבצת השביעית או השמינית. עכשיו, המשחק לעולם לא יכול להסתיים בתיקו. במוקדם או במאוחר אחד הצריחים חייב ליפול, אלא אם כן, כמובן, שני השחקנים מבצעים את האבסורד של לא לנסות לנצח. הטריק לנצח הוא פשוט להפליא כשאתה יודע אותו. האם אתה יכול לפתור את החידה? מקורות:

  • חידת הסיגר

    הצעתי פעם את החידה הבאה במועדון לונדוני, ולתקופה ניכרת היא ספגה את תשומת הלב של החברים. הם לא הצליחו להבין אותה, וחשבו שהיא בלתי אפשרית לפתרון. ובכל זאת, כפי שאראה, התשובה פשוטה להפליא.

    שני אנשים יושבים ליד שולחן מרובע. אחד מניח סיגר רגיל (שטוח בקצה אחד, מחודד בקצה השני) על השולחן, ואז השני עושה את אותו הדבר, וכן הלאה לסירוגין, בתנאי שאף סיגר לא יגע באחר. איזה שחקן יצליח להניח את הסיגר האחרון, בהנחה שכל אחד מהם ישחק בצורה הטובה ביותר האפשרית? גודל פני השולחן וגודל הסיגר אינם נתונים, אך כדי לשלול את התשובה המגוחכת שהשולחן עשוי להיות כה קטן עד שהוא יכול להכיל רק סיגר אחד, נאמר שהשולחן לא יהיה קטן מ- `2` רגל מרובע והסיגר לא יותר מ- `4`½ אינץ' אורך. עם ההגבלות האלה אתה יכול לקחת כל מימד שתרצה. כמובן שאנו מניחים שכל הסיגרים זהים לחלוטין בכל מובן. האם השחקן הראשון או השחקן השני ינצח?

    מקורות:

  • שמונה אסירים עליזים

     

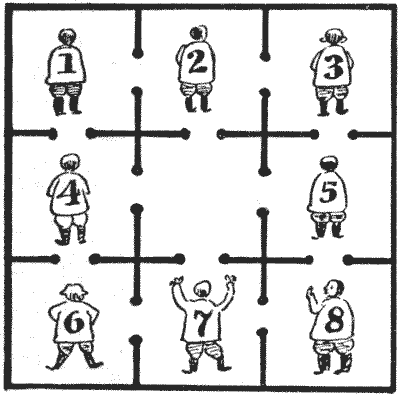
    האיור מציג תוכנית של בית סוהר המכיל תשעה תאים, כולם מקושרים זה לזה באמצעות פתחי דלתות. לשמונת האסירים יש מספרים על גבם, ומותר לכל אחד מהם להתעמל בכל תא שמתפנה, בכפוף לכלל שבאף זמן נתון לא יהיו שני אסירים באותו תא. המלך העליז שבתחום שלטונו היה ממוקם בית הסוהר הציע להם נוחיות מיוחדות בערב חג המולד אחד, אם, מבלי להפר את הכלל הזה, הם יוכלו למקם את עצמם כך שמספריהם ייצרו ריבוע קסם.

    כעת, לאסיר מספר `7` היה ידע רב על ריבועי קסם, ולכן הוא פיתח תוכנית ובחר באופן טבעי בשיטה המהירה ביותר—כלומר, כזו הכוללת את המספר הקטן ביותר האפשרי של מעברים מתא לתא. אבל אחד האנשים היה ממורמר, עקשן (בלתי מתאים לחלוטין לחברתם של חבריו העליזים), והוא סירב לצאת מתאו או לקחת חלק כלשהו בהליכים. אבל מספר `7` היה שווה ערך לחלוטין למצב החירום, וגילה שהוא עדיין יכול לעשות את מה שנדרש במספר המועט ביותר האפשרי של מהלכים, מבלי להטריד את הבהמה לעזוב את תאו. החידה היא להראות איך הוא עשה זאת, ואגב כך, לגלות איזה אסיר היה טיפש ועקשן כל כך. האם תוכלו למצוא את הבחור?

    מקורות:

  • הצינוק הספרדי

    לא רחוק מחמישים מייל מקדיז ניצב בימי הביניים מבצר, שכל עקבותיו נעלמו במשך מאות שנים. בין שאר המאפיינים המעניינים, המבצר הזה הכיל צינוק לא נעים במיוחד, המחולק לשישה עשר תאים, כולם מתקשרים זה עם זה, כפי שמוצג באיור.

    עתה, המושל היה עליז, וחובב חידות גדול. יום אחד הוא הלך לצינוק ואמר לאסירים, "בחיי!" (או המקבילה שלו בספרדית) "כולכם תשוחררו אם תוכלו לפתור את החידה הזו. עליכם לסדר את עצמכם בשישה עשר התאים כך שהמספרים על גבכם יהוו ריבוע קסם שבו כל טור, כל שורה וכל אחד משני האלכסונים יסתכמו לאותו מספר. רק זכרו זאת: שאף אחד מכם לא יהיה ביחד באותו תא."

    אחד האסירים, לאחר שעבד על הבעיה במשך יומיים או שלושה, עם חתיכת גיר, לקח על עצמו להשיג את חירותו וחירות חבריו האסירים אם הם ילכו בעקבות הוראותיו ויעברו דרך הפתח מתא לתא בסדר שבו יקרא את המספרים שלהם. 

     

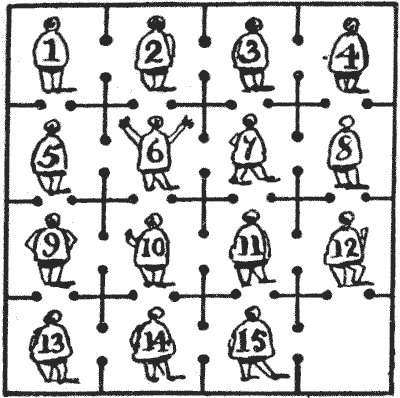
    הוא הצליח בניסיונו, ומה שמרשים יותר, כך נראה מהתיאור של שיטתו שנרשם בכתב היד העתיק שלפניי, שהוא עשה זאת במספר המהלכים המועט ביותר האפשרי. הקורא מתבקש להראות מה היו המהלכים האלה.

    מקורות:

  • מי היה הראשון?

    אנדרסון, ביגס וקרפנטר שהו יחד במקום ליד הים. יום אחד הם יצאו בסירה והיו במרחק מייל אחד מהחוף כאשר נורתה רובה לעברם. מדוע או על ידי מי נורתה הירייה למרבה המזל לא מעניין אותנו, מכיוון שאין מידע על נקודות אלה, אך מהעובדות שאספתי נוכל להשיג חומר לפאזל קטן וסקרן למתחילים.

    נראה שאנדרסון רק שמע את קול הירי, ביגס רק ראה את העשן, וקרפנטר רק ראה את הכדור פוגע במים לידם. כעת, עולה השאלה: מי מהם ידע ראשון על ירי הרובה?

    נושאים:
    לוגיקה -> הגיון
    מקורות:

  • חידת השבת

    נתקלתי בחידה קטנה זו בספר ישן. אני תוהה כמה קוראים יראו את הפתרון שהמחבר התכוון אליו. 

    הנוצרים את היום הראשון בשבוע כשבת יחזיקו;
    היהודים את השביעי, כפי שעשו מקדמת דנא;
    הטורקים את השישי, כפי שנאמר לנו לעתים קרובות.
    כיצד יכולים שלושתם, באותו מקום ויום,
    שלכל אחד תהיה השבת האמיתית שלו? אמור, אני מתפלל.

    מקורות: