לוגיקה, הגיון
קטגוריה זו מדגישה כישורי חשיבה לוגית כלליים, המיושמים לעיתים קרובות בחידות או תרחישים שאינם פורמליים לחלוטין. היא כוללת דדוקציה, הסקה, זיהוי תבניות והסקת מסקנות מבוססות ממידע נתון. יש חפיפה עם לוגיקה פורמלית אך היא יכולה להיות רחבה יותר.
פרדוקסים-
סובב את החוף
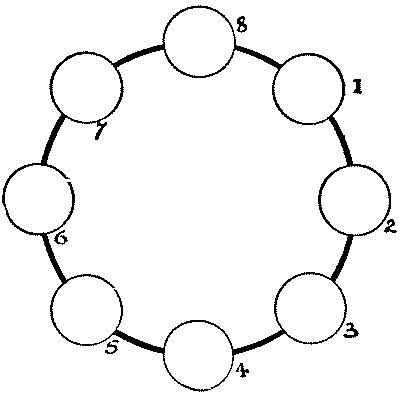 הנה חידה שלדעתי תהיה משעשעת כמו שהיא מלמדת. נתון לנו מעגל של שמונה עיגולים. כאשר עיגול `8` ריק, עלינו לכתוב את שמה של עיר נמל בת שבע אותיות בממלכה המאוחדת באופן הזה. געו בעיגול ריק עם העיפרון שלכם, ואז קפצו מעל שני עיגולים בכל כיוון מסביב למעגל, וכתבו את האות הראשונה. לאחר מכן געו בעיגול ריק אחר, קפצו מעל שני עיגולים, וכתבו את האות השנייה. המשיכו באופן דומה עם שאר האותיות בסדר הנכון שלהן עד שתשלימו את המילה. לדוגמה, נניח שנבחר ב-"Glasgow," ונמשיך כדלקמן: `6`—`1, 7`—`2, 8`—`3, 7`—`4, 8`—`5`, מה שאומר שאנחנו נוגעים ב-`6`, קופצים מעל `7`, וכותבים "G" על `1`; לאחר מכן נוגעים ב-`7`, קופצים מעל `8` ו-`1`, וכותבים "l" על `2`; וכן הלאה. יתברר שאחרי שכתבנו את חמש האותיות הראשונות - "Glasg" - כמו לעיל, אנחנו לא יכולים להמשיך הלאה. או שיש משהו לא בסדר עם "Glasgow," או שלא הצלחנו לבצע את הקפיצות שלנו כראוי. האם תוכלו לרדת לשורש התעלומה?
מקורות:
הנה חידה שלדעתי תהיה משעשעת כמו שהיא מלמדת. נתון לנו מעגל של שמונה עיגולים. כאשר עיגול `8` ריק, עלינו לכתוב את שמה של עיר נמל בת שבע אותיות בממלכה המאוחדת באופן הזה. געו בעיגול ריק עם העיפרון שלכם, ואז קפצו מעל שני עיגולים בכל כיוון מסביב למעגל, וכתבו את האות הראשונה. לאחר מכן געו בעיגול ריק אחר, קפצו מעל שני עיגולים, וכתבו את האות השנייה. המשיכו באופן דומה עם שאר האותיות בסדר הנכון שלהן עד שתשלימו את המילה. לדוגמה, נניח שנבחר ב-"Glasgow," ונמשיך כדלקמן: `6`—`1, 7`—`2, 8`—`3, 7`—`4, 8`—`5`, מה שאומר שאנחנו נוגעים ב-`6`, קופצים מעל `7`, וכותבים "G" על `1`; לאחר מכן נוגעים ב-`7`, קופצים מעל `8` ו-`1`, וכותבים "l" על `2`; וכן הלאה. יתברר שאחרי שכתבנו את חמש האותיות הראשונות - "Glasg" - כמו לעיל, אנחנו לא יכולים להמשיך הלאה. או שיש משהו לא בסדר עם "Glasgow," או שלא הצלחנו לבצע את הקפיצות שלנו כראוי. האם תוכלו לרדת לשורש התעלומה?
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 226
-
חידת ההחלפה
הנה חידה קטנה ומשעשעת עם העברת חיילים. אתה צריך רק שנים עשר חיילים—שישה מצבע אחד, המסומנים A, C, E, G, I ו-K, והשישה האחרים מסומנים B, D, F, H, J ו-L. אתה מניח אותם תחילה על הדיאגרמה, כפי שמוצג באיור, והחידה היא להביא אותם לסדר אלפביתי רגיל, כדלקמן:—
A B C D E F G H I J K L המהלכים מתבצעים על ידי החלפות של צבעים מנוגדים העומדים על אותו קו. כך, G ו-J יכולים להחליף מקומות, או F ו-A, אבל אינך יכול להחליף את G ו-C, או F ו-D, מכיוון שבמקרה אחד שניהם לבנים ובמקרה השני שניהם שחורים. האם אתה יכול להביא את הסידור הנדרש בשבע עשרה החלפות?
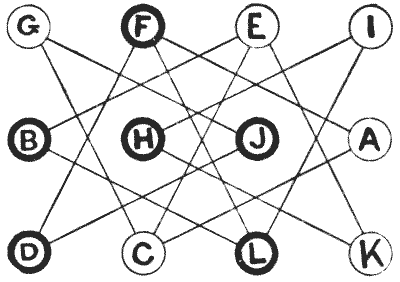
אי אפשר לעשות זאת בפחות מהלכים. החידה באמת הרבה יותר קלה ממה שהיא נראית, אם תוקפים אותה כראוי.
מקורות:נושאים:קומבינטוריקה -> אינווריאנטים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 234
-
בנים ובנות
אם תסמנו עשרה חלוקות על דף נייר כדי לייצג את הכיסאות, ותשתמשו בשמונה אסימונים ממוספרים עבור הילדים, יהיה לכם בילוי מרתק. תנו למספרים האי-זוגיים לייצג בנים ולמספרים הזוגיים בנות, או שתוכלו להשתמש באסימונים משני צבעים, או במטבעות.
החידה היא להסיר שני ילדים היושבים בכיסאות סמוכים ולהניח אותם בשני כיסאות ריקים, כאשר הם מחליפים צדדים תחילה; לאחר מכן הסירו זוג ילדים שני מכיסאות סמוכים והניחו אותם בשני הכיסאות הפנויים כעת, כשהם מחליפים צדדים; וכן הלאה, עד שכל הבנים יהיו ביחד וכל הבנות ביחד, כאשר שני הכיסאות הריקים בקצה אחד כמו עכשיו. כדי לפתור את החידה, עליכם לעשות זאת בחמישה מהלכים. שני הילדים חייבים תמיד להילקח מכיסאות הצמודים זה לזה; וזכרו את הנקודה החשובה של החלפת הצדדים בין שני הילדים, שכן זהו המאפיין הייחודי של החידה. על ידי "החלפת צדדים" אני פשוט מתכוון שאם, לדוגמה, תזיזו תחילה את `1` ו-`2` לכיסאות הריקים, אז הכיסא הראשון (החיצוני) יאוכלס על ידי `2` והשני על ידי `1`.
מקורות: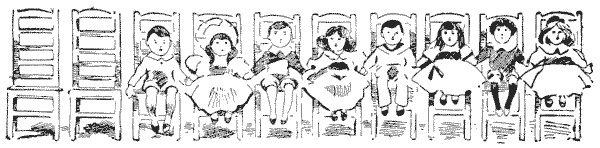
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 237
-
סידור קופסאות הריבה
קרה שראיתי ילדה קטנה ממיינת ריבות בארון עבור אמה. היא הניחה כל סוג ריבה בנפרד על המדפים. שמתי לב שהיא לקחה צנצנת שזיפים ביד אחת וצנצנת דומדמניות ביד השנייה והחליפה ביניהן; אחר כך היא החליפה תות שדה עם פטל, וכן הלאה. היה מעניין לראות כמה טרחה מיותרת היא נתנה לעצמה על ידי ביצוע יותר החלפות ממה שהיה צורך, וחשבתי שזה יכול להפוך לחידה טובה.

כפי שניתן לראות באיור, דורותי הקטנה צריכה לתפעל עשרים וארבע קופסאות ריבה גדולות במספר תאים תואם. היא רוצה לסדר אותן בסדר מספרי נכון—כלומר, `1, 2, 3, 4, 5, 6` על המדף העליון, `7, 8, 9, 10, 11, 12` על המדף הבא, וכן הלאה. עכשיו, אם היא תמיד לוקחת קופסה אחת ביד ימין ואחת ביד שמאל ומחליפה ביניהן, כמה מההחלפות האלה יהיו נחוצות כדי לסדר את כל קופסאות הריבה בסדר הנכון? באופן טבעי היא תחליף קודם את `1` ואת `3`, אחר כך את `2` ואת `3`, ואז יהיו לה שלוש הקופסאות הראשונות במקומן. איך היית מייעץ לה להמשיך מכאן? הניחו כמה אסימונים ממוספרים על דף נייר המחולק למשבצות עבור התאים, ותגלו שזו חידה משעשעת.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 238
-
מסע האופניים
שני רוכבי אופניים התייעצו במפת דרכים לקראת טיול קצר משותף. העיגולים מייצגים ערים, וכל הדרכים הטובות מיוצגות על ידי קווים. הם מתחילים מהעיר עם הכוכב, ועליהם להשלים את הטיול שלהם ב-E. אבל לפני שהם מגיעים לשם הם רוצים לבקר בכל עיר אחרת פעם אחת, ורק פעם אחת. זו הבעיה. מר ספייסר אמר, "אני בטוח שנוכל למצוא דרך לעשות זאת;" אבל מר מגס השיב, "בשום אופן, אני בטוח." עכשיו, מי מהם צדק? קחו את העיפרון שלכם ובדקו אם תוכלו למצוא דרך לעשות זאת. כמובן שעליכם להישאר בדרכים המצוינות.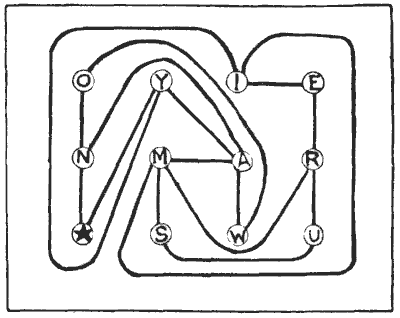 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 248
-
הטיול הגדול
אחת החידות היומיומיות של החיים היא תכנון מסלולים. אם אתם יוצאים לחופשה על אופניים, או לטיול מוטורי, תמיד עולה השאלה כיצד לנצל את הזמן והמשאבים שלכם בצורה הטובה ביותר. החלטתם להגיע למקום מסוים, לכלול ביקורים בעיר כזו וכזו, לנסות לראות משהו מעניין במיוחד במקום אחר, ואולי לנסות לבקר חבר ותיק בנקודה שלא תוציא אתכם בהרבה מהדרך. אז אתם צריכים לתכנן את המסלול שלכם כדי להימנע מכבישים גרועים, אזורים לא מעניינים, ואם אפשר, מהצורך לחזור באותה דרך שבה נסעתם. עם מפה לפניכם, ניגשים לפתרון החידה המעניינת. אציג לכם שאלה קטנה המבוססת על קווים אלה.
אני מציג מפה גסה של מדינה—אין צורך לומר איזו מדינה—העיגולים מייצגים ערים והקווים המקווקווים את מסילות הברזל המחברות ביניהן. עכשיו, בעיר המסומנת A חי אדם שנולד שם, ובמשך כל חייו מעולם לא עזב את מקום הולדתו. מנעוריו הוא היה חרוץ מאוד, דבק בעקביות במקצועו, ולא היה לו רצון לשוטט בחוץ. עם זאת, בהגיעו לגיל חמישים הוא החליט לראות קצת מהמדינה שלו, ובמיוחד לבקר חבר ותיק מאוד שגר בעיר המסומנת Z. מה שהוא הציע היה כזה: שהוא יתחיל מביתו, ייכנס לכל עיר פעם אחת בלבד, ויסיים את מסעו ב-Z. מכיוון שהוא החליט לבצע את הטיול הגדול הזה ברכבת בלבד, הוא התקשה קצת לתכנן את המסלול שלו, אבל בסופו של דבר הוא הצליח לעשות זאת. איך הוא הצליח? אל תשכחו שצריך לבקר בכל עיר פעם אחת, ולא יותר מפעם אחת.
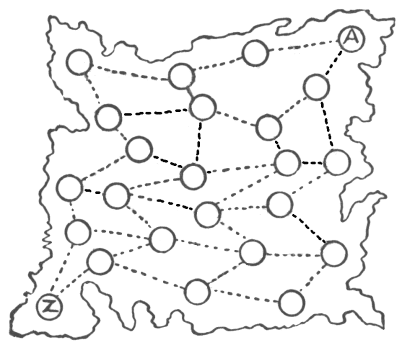 מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 250
-
מים, גז וחשמל
ישנם כחצי תריסר חידות, עתיקות כימי ההיסטוריה, שצצות ועולות תדיר, וכמעט שאין חודש בשנה שלא מביא עמו פניות בנוגע לפתרונן. מדי פעם אחת מהן, שאדם חשב שהיא הר געש כבוי, מתפרצת בצורה מפתיעה. קיבלתי מספר יוצא דופן של מכתבים בנוגע לחידה העתיקה שכיניתי "מים, גז וחשמל". היא עתיקה בהרבה מתאורת חשמל, או אפילו גז, אבל הלבוש החדש מעדכן אותה. החידה היא להניח מים, גז וחשמל, מ-W, G ו-E, לכל אחד משלושת הבתים, A, B ו-C, מבלי שאף צינור יחצה צינור אחר. קחו את העיפרון וציירו קווים המראים כיצד יש לעשות זאת. עד מהרה תמצאו את עצמכם נתקלים בקשיים.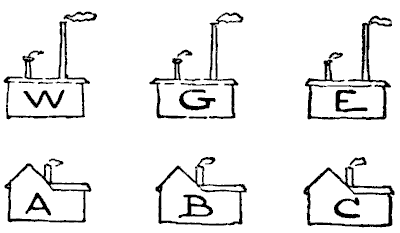 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 251
-
חֲמֵשׁ עֶשְׂרֵה כְּבָשִׂים
אנציקלופדיה מסוימת הציגה את הבעיה המוזרה הבאה, כך שמעתי: "הנח חמש עשרה כבשים בארבעה מכלאות כך שיהיה אותו מספר כבשים בכל מכלאה." לא ניתנה תשובה כלשהי, אז החלטתי לחקור את הנושא. ראיתי שבהתמודדות עם תפוחים או לבנים, הדבר ייראה בלתי אפשרי לחלוטין, מכיוון שארבע פעמים כל מספר חייב להיות מספר זוגי, בעוד שחמש עשרה הוא מספר אי-זוגי. לכן חשבתי שחייבת להיות תכונה מסוימת לכבשים שלא הייתה ידועה בדרך כלל. אז החלטתי לראיין כמה חקלאים בנושא. הראשון ציין שאם נכניס מכלאה אחת בתוך השנייה, כמו הטבעות של מטרה, ונניח את כל הכבשים במכלאה הקטנה ביותר, הכל יהיה בסדר. אבל התנגדתי לכך, כי אתה מודה שאתה מניח את כל הכבשים במכלאה אחת, לא בארבע מכלאות. האיש השני אמר שאם אני אניח ארבע כבשים בכל אחת משלוש מכלאות ושלוש כבשים במכלאה האחרונה (כלומר חמש עשרה כבשים בסך הכל), ולאחת הכבשות במכלאה האחרונה יהיה טלה במהלך הלילה, יהיה אותו מספר בכל מכלאה בבוקר. גם זה לא סיפק אותי. החקלאי השלישי אמר, "יש לי ארבע מכלאות גדר בשדה שלי, ועדר קטן של כבשים מסורסים, אז אם רק תרד איתי למטה אני אראה לך איך זה נעשה." האיור מתאר את ידידי כשהוא עומד להדגים לי את העניין. ההסבר הבהיר שלו היה כנראה זה שהיה במוחו של כותב המאמר באנציקלופדיה. מה זה היה? האם אתה יכול להניח את חמש עשרה הכבשים האלה?
מקורות:נושאים:אלגברה -> בעיות מילוליות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים
החקלאי השלישי אמר, "יש לי ארבע מכלאות גדר בשדה שלי, ועדר קטן של כבשים מסורסים, אז אם רק תרד איתי למטה אני אראה לך איך זה נעשה." האיור מתאר את ידידי כשהוא עומד להדגים לי את העניין. ההסבר הבהיר שלו היה כנראה זה שהיה במוחו של כותב המאמר באנציקלופדיה. מה זה היה? האם אתה יכול להניח את חמש עשרה הכבשים האלה?
מקורות:נושאים:אלגברה -> בעיות מילוליות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 262
-
החלון של האב המנזר
לפני שנים רבות, האב המנזר מסנט אדמונדסברי, כתוצאה מ"מסירות חזקה מדי לראשו," חלה ולא היה מסוגל לעזוב את מיטתו. כששכב ער, מטלטל את ראשו באי שקט מצד לצד, הנזירים הקשובים הבחינו שמשהו מטריד את מחשבותיו; אך איש לא העז לשאול מה זה יכול להיות, כי האב המנזר היה בעל אופי קשוח, ומעולם לא סבל סקרנות. לפתע קרא לאב ג'ון, והנזיר המכובד ההוא מיהר למיטתו.
"אב ג'ון," אמר האב המנזר, "האם אתה יודע שנולדתי לעולם הנורא הזה בערב חג המולד?
"הנזיר הנהן בהסכמה.
"והאם לא אמרתי לך לעתים קרובות, שנולדתי בערב חג המולד, שאין לי אהבה לדברים שהם אי-זוגיים? תסתכל שם!"
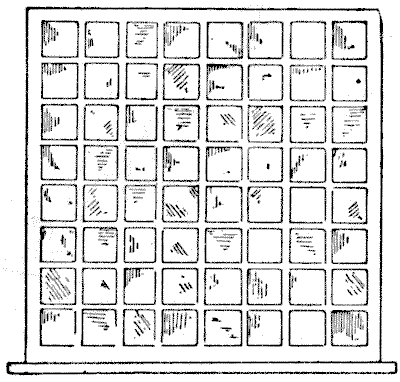
האב המנזר הצביע על חלון המעונות הגדול, שממנו אני נותן סקיצה. הנזיר הביט, והיה נבוך.
"האם אינך רואה ששישים וארבעת האורות מסתכמים למספר זוגי אנכית ואופקית, אך כל הקווים האלכסוניים, למעט ארבעה עשר, הם מספר שהוא אי-זוגי? מדוע זה?"
"אכן, אדוני האב המנזר, זה טבע הדברים, ואי אפשר לשנות זאת."
"לא, אבל זה יש ישתנה. אני מצווה עליך שחלק מהאורות ייחסמו היום, כך שלכל קו יהיה מספר זוגי של אורות. ראה שזה נעשה ללא דיחוי, שמא המרתפים יינעלו לחודש וצרות קשות אחרות יפקדו אותך."
אב ג'ון היה חסר אונים, אך לאחר התייעצות עם מישהו שהיה בקיא בתעלומות מוזרות, נמצאה דרך לספק את גחמתו של האב המנזר. אילו אורות נחסמו, כך שאלה שנותרו הסתכמו למספר זוגי בכל קו אופקית, אנכית ואלכסונית, תוך גרימת ההפרעה המינימלית האפשרית לאור?
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 292
-
שמונה מלכות
המלכה היא ללא ספק הכלי החזק ביותר על לוח השחמט. אם תניח אותה על אחד מארבעת הריבועים במרכז הלוח, היא תוקפת לא פחות מעשרים ושבעה ריבועים אחרים; ואם תנסה להחביא אותה בפינה, היא עדיין תתקוף עשרים ואחד ריבועים. ניתן להניח שמונה מלכות על הלוח כך שאף מלכה לא תתקוף מלכה אחרת, וזוהי חידה ותיקה (שהועלתה לראשונה על ידי נאוק ב-`1850`, ויש לה ספרות משלה) לגלות בכמה דרכים שונות ניתן לעשות זאת. אני מראה דרך אחת בתרשים, ויש בסך הכל שתים עשרה דרכים שונות במהותן. שנים עשר אלה מניבים תשעים ושתיים דרכים אם אנו רואים היפוכים ושיקופים כשונים. התרשים הוא במידה מסוימת סידור סימטרי. אם תהפוך את הדף, הוא ישחזר את עצמו בדיוק; אבל אם תסתכל עליו כשאחד הצדדים האחרים בתחתית, תקבל דרך אחרת שאינה זהה. ואז אם תשקף את שתי הדרכים האלה במראה, תקבל עוד שתי דרכים. כעת, כל אחד-עשר הפתרונות האחרים אינם סימטריים, ולכן ניתן להציג כל אחד מהם בשמונה דרכים על ידי היפוכים ושיקופים אלה. כך יובן מדוע שנים עשר הפתרונות השונים במהותם מניבים רק תשעים ושניים סידורים, כפי שאמרתי, ולא תשעים וששה, כפי שהיה קורה אילו כל שנים עשר לא היו סימטריים. כדאי שתהיה הבנה ברורה בעניין ההיפוכים והשיקופים כאשר עוסקים בחידות על לוח השחמט. האם הקורא יכול להניח את שמונה המלכות על הלוח כך שאף מלכה לא תתקוף מלכה אחרת, וכך שאף שלוש מלכות לא יהיו בקו ישר בכל כיוון אלכסוני? מבט נוסף בתרשים יראה שהסידור הזה לא יענה על התנאים, כי בשני הכיוונים המצוינים בקווים המקווקווים יש שלוש מלכות בקו ישר. יש רק דרך אחת מתוך שתים עשרה הדרכים הבסיסיות שתפתור את החידה. האם אתה יכול למצוא את זה?
מקורות:
האם הקורא יכול להניח את שמונה המלכות על הלוח כך שאף מלכה לא תתקוף מלכה אחרת, וכך שאף שלוש מלכות לא יהיו בקו ישר בכל כיוון אלכסוני? מבט נוסף בתרשים יראה שהסידור הזה לא יענה על התנאים, כי בשני הכיוונים המצוינים בקווים המקווקווים יש שלוש מלכות בקו ישר. יש רק דרך אחת מתוך שתים עשרה הדרכים הבסיסיות שתפתור את החידה. האם אתה יכול למצוא את זה?
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 300