לוגיקה, הגיון
קטגוריה זו מדגישה כישורי חשיבה לוגית כלליים, המיושמים לעיתים קרובות בחידות או תרחישים שאינם פורמליים לחלוטין. היא כוללת דדוקציה, הסקה, זיהוי תבניות והסקת מסקנות מבוססות ממידע נתון. יש חפיפה עם לוגיקה פורמלית אך היא יכולה להיות רחבה יותר.
פרדוקסים-
השוטה של הכפר
אדם שנון שטייל ארוכות באזור הכפרי נתקל בבור יושב על סולם. כיוון שהג'נטלמן לא היה בטוח לחלוטין בדרכו, הוא חשב לשאול את התושב המקומי; אך במבט ראשון הוא קפץ מהר מדי למסקנה שהוא נפל על אידיוט הכפר. לכן הוא החליט לבחון את האינטליגנציה של הבחור על ידי כך שקודם כל ישאל אותו את השאלה הפשוטה ביותר שהוא יכול לחשוב עליה, שהייתה, "איזה יום בשבוע זה, ידידי הטוב?" התשובה החכמה שהוא קיבל הייתה:—
"כאשר היום שאחרי מחר הוא אתמול, היום יהיה רחוק מיום ראשון כפי שהיום היה רחוק מיום ראשון כאשר היום שלפני אתמול היה מחר."
האם הקורא יכול לומר איזה יום בשבוע זה היה? די ברור שהאיש הכפרי לא היה טיפש כמו שנראה. הג'נטלמן המשיך בדרכו מבולבל אך חכם יותר.
מקורות: -
חבית הבירה
אדם קנה כמות מוזרה של יין בחביות וחבית אחת המכילה בירה. אלה מוצגים באיור, המסומנים במספר הגלונים שכל חבית הכילה. הוא מכר כמות מהיין לאדם אחד וכמות כפולה לאחר, אך שמר את הבירה לעצמו. החידה היא לציין איזו חבית מכילה בירה. האם אתה יכול לומר איזו מהן זו? כמובן, האיש מכר את החביות בדיוק כפי שקנה אותן, מבלי לתפעל בשום צורה את התכולה.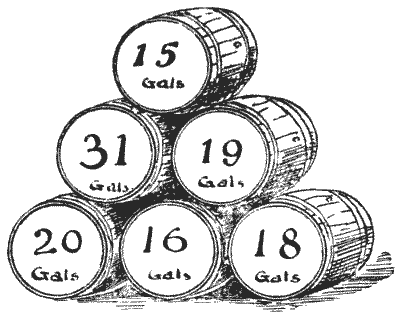 מקורות:נושאים:אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 אלגברה -> בעיות מילוליות לוגיקה -> הגיון
מקורות:נושאים:אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 אלגברה -> בעיות מילוליות לוגיקה -> הגיון -
חידת הלוקרים
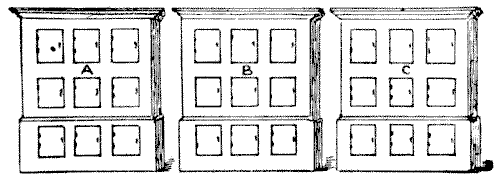
לאיש היו במשרדו שלושה ארונות, שבכל אחד מהם תשעה לוקרים, כפי שמוצג בדיאגרמה. הוא הורה לפקיד שלו להציב ספרה שונה על כל לוקר בארון A, ולעשות את אותו הדבר בארון B ובארון C. מכיוון שמותר לנו כאן לקרוא לאפס ספרה, ולא נאסר עליו להשתמש באפס כמספר, ברור שהייתה לו האפשרות להשמיט כל אחת מעשר הספרות מכל ארון.
כעת, המעסיק לא אמר שהלוקרים ימוספרו בסדר מספרי כלשהו, והוא הופתע לגלות, לאחר שהעבודה הסתיימה, שהספרות כנראה עורבבו באופן אקראי. כשקרא לפקיד שלו להסבר, הנער האקסצנטרי הצהיר שהעלתה בדעתו המחשבה לסדר את הספרות כך שבכל מקרה הן יצרו תרגיל חיבור פשוט, כאשר שתי השורות העליונות של הספרות יוצרות את הסכום בשורה התחתונה. אבל הנקודה המפתיעה ביותר הייתה זו: שהוא סידר אותן כך שהחיבור ב-A נתן את הסכום הקטן ביותר האפשרי, שהחיבור ב-C נתן את הסכום הגדול ביותר האפשרי, וכי כל תשע הספרות בסך הכל בשלושת הסכומים היו שונות. החידה היא להראות כיצד ניתן לעשות זאת. אין לאפשר עשרונים והאפס אינו יכול להופיע במקום המאות.
מקורות: -
חידת המאה
האם תוכלו לכתוב `100` בצורה של מספר מעורב, תוך שימוש בכל תשע הספרות פעם אחת בלבד? המתמטיקאי הצרפתי המכובד, אדוארד לוקאס, מצא שבע דרכים שונות לעשות זאת, והביע את ספקותיו לגבי קיומן של דרכים אחרות. למעשה יש בדיוק אחת-עשרה דרכים ולא יותר. הנה אחת מהן, `91 5742/638`. בתשע מהדרכים האחרות יש באופן דומה שתי ספרות בחלק השלם של המספר, אך לביטוי האחד-עשר יש רק ספרה אחת שם. האם הקורא יכול למצוא את הצורה האחרונה הזו?
מקורות:נושאים:תורת המספרים -> חשבון השאריות -> סימני חלוקה לוגיקה -> הגיון אריתמטיקה -> שברים קומבינטוריקה -> בדיקת מקרים -> תהליכים -
צביעת עמודי התאורה
טים מרפי ופאט דונובן הועסקו על ידי הרשויות המקומיות לצבוע את עמודי התאורה ברחוב מסוים. טים, שהיה קם מוקדם, הגיע ראשון לעבודה, וצבע שלושה עמודים בצד הדרומי כאשר פאט הגיע והצביע על כך שהחוזה של טים היה עבור הצד הצפוני. אז טים התחיל מחדש בצד הצפוני ופאט המשיך בצד הדרומי. כאשר פאט סיים את הצד שלו, הוא עבר את הרחוב וצבע שישה עמודים עבור טים, ואז העבודה הסתיימה. מכיוון שהיה מספר שווה של עמודי תאורה בכל צד של הרחוב, השאלה הפשוטה היא: איזה איש צבע יותר עמודי תאורה, ובכמה יותר? מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 103
-
שיווק של שבת
הנה מקרה משעשע קטן של שיווק, שלמרות שהוא עוסק במספר רב של פריטי כסף, מוביל לשאלה בעלת אופי שונה לחלוטין. ארבעה זוגות נשואים נסעו לכפר שלהם בשבת בערב האחרון כדי לעשות קניות קטנות. הם היו צריכים להיות מאוד חסכוניים, כי ביחד היו להם רק ארבעים מטבעות שילינג. העניין הוא, אן הוציאה `1`s., מרי הוציאה `2`s., ג'יין הוציאה `3`s., וקייט הוציאה `4`s. הגברים היו קצת יותר פזרניים מנשותיהם, כי נד סמית' הוציא כמו אשתו, טום בראון הוציא פי שניים מאשתו, ביל ג'ונס הוציא פי שלושה מאשתו, וג'ק רובינסון הוציא פי ארבעה מאשתו. בדרך הביתה מישהו הציע שהם יחלקו את מה שנשאר להם באופן שווה ביניהם. זה נעשה, והשאלה המטרידה היא פשוט זו: מה היה שם המשפחה של כל אישה? האם אתה יכול להתאים את ארבעת הזוגות?
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 141
-
מִכְלָא הַצֹּאן
זהו עובדה מוזרה שהתשובות שניתנות תמיד לכמה מהחידות הידועות ביותר המופיעות בכל ספר קטן של שעשועי בית שפורסם בחמישים או מאה השנים האחרונות הן או בלתי מספקות לחלוטין או שגויות בבירור. עם זאת, נראה שאף אחד לא מבחין בפגמים שלהן. הנה דוגמה: - לחקלאי היה מכלאה העשויה מחמישים גדרות, המסוגלת להכיל רק מאה כבשים. נניח שהוא רצה להגדיל אותו מספיק כדי להכיל כפול ממספר זה, כמה גדרות נוספות הוא צריך? מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 193
-
חידת החגב
הועלתה סברה שהחידה הזו הייתה חביבה מאוד על החניכים הצעירים של הסיטי של לונדון במאות השש-עשרה והשבע-עשרה. הקוראים בוודאי הבחינו בחגב הפליז המוזר בבורסה המלכותית. יצור ארוך שנים זה ניצל משריפות `1666` ו-`1838`. החגב, כדרכו, היה סמל של סר תומס גרשם, סוחר מכולת, שמת בשנת `1579`, ומסיבה זו הוא שימש כסמל על ידי מכולת באופן כללי. למרבה הצער עבור האגדה לגבי מקורה, החידה הופקה על ידי עצמי רק בשנת `1900`. על שנים עשר מתוך שלושה עשר הדיסקים השחורים מונחים אסימונים ממוספרים או חגבים. החידה היא להפוך את סדרם, כך שיקראו, `1, 2, 3, 4` וכו', בכיוון ההפוך, כאשר הדיסק הריק נשאר באותו מיקום כמו עכשיו. הזיזו אחד בכל פעם בכל סדר, או לדיסק הריק הסמוך או על ידי קפיצה מעל חגב אחד, כמו המהלכים בדמקה. ניתן לבצע את המהלכים או הקפיצות בכל כיוון שאפשרי בכל עת. מהם מספר המהלכים המועט ביותר שבו ניתן לעשות זאת?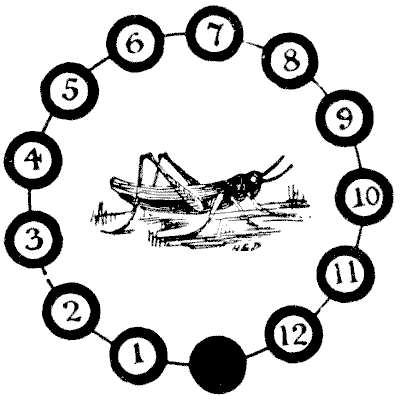 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 215
-
קושי בבית דירות
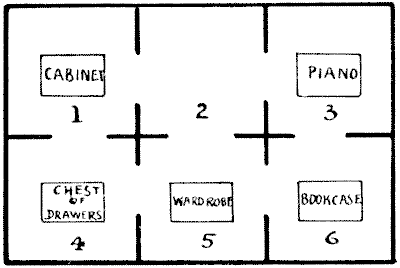 משפחת דובסון שכרה דירות בסלוקום-און-סי. היו שישה חדרים באותה קומה, כולם מחוברים, כפי שמוצג בתרשים. החדרים שהם לקחו היו מספרים `4, 5`, ו-`6`, כולם פונים לים. אבל התעוררה בעיה קטנה. מר דובסון התעקש שהפסנתר וארון הספרים יחליפו חדרים. זה היה ערמומי, כי משפחת דובסון לא הייתה מוזיקלית, אבל הם רצו למנוע מכל אחד אחר לנגן בכלי הנגינה. עכשיו, החדרים היו קטנים מאוד ופריטי הריהוט שצוינו היו גדולים מאוד, כך שלא ניתן היה להכניס שניים מהפריטים הללו לאף חדר באותו זמן. איך ניתן לבצע את ההחלפה עם מינימום עבודה? נניח, לדוגמה, שאתה מעביר תחילה את הארון לבגדים למספר `2`; אז אתה יכול להעביר את ארון הספרים למספר `5` ואת הפסנתר למספר `6`, וכן הלאה. זו חידה מרתקת, אבל לבעלת הבית היו סיבות לא להעריך אותה. נסה לפתור את הקושי שלה במספר המינימלי האפשרי של העברות עם אסימונים על דף נייר.
מקורות:
משפחת דובסון שכרה דירות בסלוקום-און-סי. היו שישה חדרים באותה קומה, כולם מחוברים, כפי שמוצג בתרשים. החדרים שהם לקחו היו מספרים `4, 5`, ו-`6`, כולם פונים לים. אבל התעוררה בעיה קטנה. מר דובסון התעקש שהפסנתר וארון הספרים יחליפו חדרים. זה היה ערמומי, כי משפחת דובסון לא הייתה מוזיקלית, אבל הם רצו למנוע מכל אחד אחר לנגן בכלי הנגינה. עכשיו, החדרים היו קטנים מאוד ופריטי הריהוט שצוינו היו גדולים מאוד, כך שלא ניתן היה להכניס שניים מהפריטים הללו לאף חדר באותו זמן. איך ניתן לבצע את ההחלפה עם מינימום עבודה? נניח, לדוגמה, שאתה מעביר תחילה את הארון לבגדים למספר `2`; אז אתה יכול להעביר את ארון הספרים למספר `5` ואת הפסנתר למספר `6`, וכן הלאה. זו חידה מרתקת, אבל לבעלת הבית היו סיבות לא להעריך אותה. נסה לפתור את הקושי שלה במספר המינימלי האפשרי של העברות עם אסימונים על דף נייר.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 220
-
חידת מוסך המכוניות
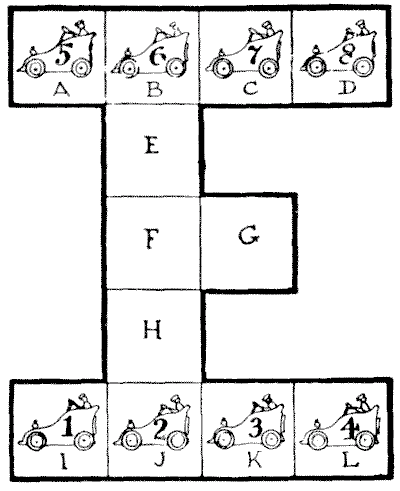
הקשיים של בעל מוסך מוסבים למעין בילוי שיש בו קסם מיוחד. כל מה שצריך זה להכין תוכנית או דיאגרמה פשוטה על דף נייר או קרטון ולמספר שמונה אסימונים, מ-`1` עד `8`. אז משפחה שלמה יכולה להיכנס לתחרות משעשעת כדי למצוא את הפתרון הטוב ביותר לקושי.
האיור מייצג את תוכנית מוסך המכוניות, עם מקום לשתים עשרה מכוניות. אבל השטח מצומצם בצורה לא נוחה, ולכן הבעלים נתקל לעתים קרובות במבוכה רבה. נניח, למשל, ששמונה המכוניות הממוספרות מ-`1` עד `8` נמצאות במקומות המוצגים, איך ניתן להזיז אותן בצורה המהירה ביותר כך ש-`1, 2, 3` ו-`4` יחליפו מקומות עם `5, 6, 7` ו-`8` — כלומר, כשהמספרים עדיין רצים משמאל לימין, כפי שהם כרגע, אבל השורה העליונה הוחלפה בשורה התחתונה? מהו המספר הקטן ביותר של מהלכים אפשריים?
מכונית אחת זזה בכל פעם, וכל מרחק נחשב למהלך אחד. כדי למנוע אי הבנות, מקומות העצירה מסומנים בריבועים, ויכולה להיות רק מכונית אחת בריבוע בכל פעם.
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 224