קומבינטוריקה, צביעות

בעיות צביעה כוללות הקצאת 'צבעים' (תוויות) לאובייקטים (כמו אזורים במפה, קדקודים/קשתות של גרף, או משבצות על לוח) בכפוף לאילוצים מסוימים (למשל, אובייקטים סמוכים חייבים להיות בצבעים שונים). שאלות שואלות האם צביעה אפשרית או מחפשות את המספר המינימלי של צבעים.

בעיה בפסיפסים

אמנות יצירת תמונות או עיצובים באמצעות חיבור חתיכות של חומרים קשים, צבועים באופן טבעי או מלאכותי, היא עתיקה מאוד. היא הייתה ידועה בוודאות בתקופת הפרעונים, ואנו מוצאים התייחסות במגילת אסתר ל"מרצפת בהט ושש ודר וסחרת". נראה כי חלק מהעבודה העתיקה הזו שהגיעה אלינו, במיוחד כמה מהפסיפסים הרומיים, מראים בבירור, גם כאשר העיצוב אינו ניכר בתחילה, כי מחשבה רבה הושקעה בסידורים שנראים לכאורה לא מסודרים. כאשר, למשל, העבודה הופקה עם מספר מוגבל מאוד של צבעים, ישנן עדויות לתחכום רב במניעת גוונים זהים המגיעים בסמיכות זה לזה. קוראות ליידי שמכירות את בניית שמיכות טלאים ידעו כמה רצוי לפעמים, כאשר הן מוגבלות בבחירת החומר, למנוע מחתיכות מאותו חומר להתקרב מדי זו לזו. כעת, החידה הזו תחול במידה שווה על שמיכות טלאים או ריצוף טסלטה.

ניתן לראות מהדיאגרמה כיצד ניתן לרצף פיסת רצפה מרובעת עם שישים ושתיים אריחים מרובעים משמונת הצבעים סגול, אדום, צהוב, ירוק, כתום, ארגמן, לבן וכחול (המצוינים באותיות הראשונות), כך שאף אריח אינו נמצא בקו אחד עם אריח צבעוני דומה, אנכית, אופקית או אלכסונית. לא ניתן יהיה להציב שישים וארבעה אריחים כאלה בתנאים אלה, אך שני הריבועים המוצלים תפוסים על ידי פתחי אוורור מברזל.

החידה היא זו. יש להסיר את שני פתחי האוורור הללו למיקומים המצוינים על ידי האריחים התחומים כהה, ושני אריחים ממוקמים בריבועי הפינה התחתונה הללו. האם אתה יכול להתאים מחדש את שלושים ושניים האריחים כך ששניים מאותו צבע עדיין לא יהיו בקו?

נושאים:
קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> צביעות
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 302
שאלה

על המעגל נתונות נקודות כחולות ואדומות. מותר להוסיף נקודה אדומה ולשנות את הצבעים של הנקודות השכנות שלה או להסיר נקודה אדומה ולשנות את הצבעים של הנקודות השכנות שלה בעבר (אסור להשאיר פחות מ-2 נקודות על המעגל). הוכח/י כי אי אפשר להעביר רק ע"י הפעולות האלה מעגל עם שתי נקודות אדומות למעגל עם שתי נקודות כחולות.
ק. קזרנובסקי

נושאים:
קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> אינווריאנטים אלגברה לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות תורת הקבוצות קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> צביעות -> צביעת שחמט
מקורות:
- תחרות הערים, תש"מ, עיקרית, אביב שאלה 1
שאלה

האם ניתן לרצף לוח `5xx5` על ידי אבני דומינו?

הערה: גודל של משבצת הלוח תואם לגודל המשבצת של דומינו.

נושאים:
קומבינטוריקה -> גאומטריה קומבינטורית לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות קומבינטוריקה -> צביעות -> צביעת שחמט
שאלה

פרש שח יצא מהמשבצת `a1`, ותוך מספר מהלכים חזר לאותה המשבצת.

האם יתכן שהפרש ביצע מספר אי-זוגי של מהלכים?

התחברו כאן לאתר על מנת לקבל את הרמז

נושאים:
קומבינטוריקה -> אינווריאנטים לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות קומבינטוריקה -> צביעות -> צביעת שחמט
שאלה

פרש שח יצא מהמשבצת `a1` והגיע למשבצת `h8`. האם יתכן שבדרך הוא ביקר בכל משבצות הלוח בדיוק פעם אחת?

התחברו כאן לאתר על מנת לקבל את הרמז

נושאים:
קומבינטוריקה -> ספירה כפולה קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה -> הוכחה בשלילה קומבינטוריקה -> צביעות -> צביעת שחמט
שאלה

מלוח שחמט גוזרים שתי פינות מנוגדות (השדות `a1` ו-`h8`, למשל). האם תוכלו לרצף את הלוח שנשאר על ידי אבני דומינו?

התחברו כאן לאתר על מנת לקבל את הרמז

נושאים:
קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> התאמות לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה -> הוכחה בשלילה קומבינטוריקה -> צביעות -> צביעת שחמט חידות ורבוסים
שאלה

הוכיחו כי לא ניתן לחתוך את הצורה הנתונה לאבני דומינו:

נושאים:
קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> התאמות תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה -> הוכחה בשלילה קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
שאלה

האם תוכלו לחתוך את הצורה שבצד שמאל לשש צורות כמו הצורה בצד ימין?

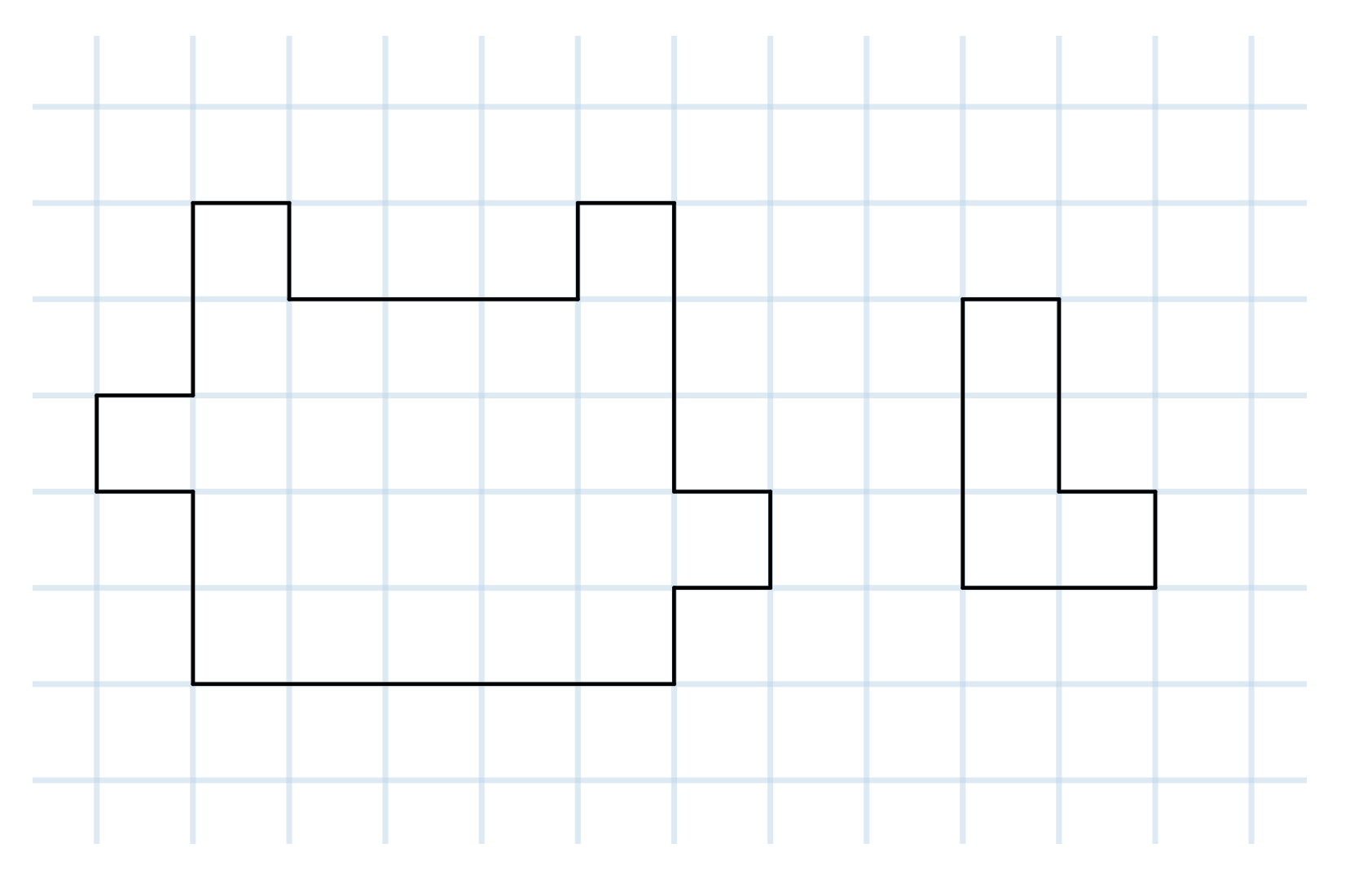נושאים:
קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> התאמות הוכחה ודוגמה קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
שאלה

ברשותו של שלומי לוח שחמט וקובייה שגודל הפאה שלה הוא כמו גודל של משבצת הלוח. שלומי רוצה לצבוע את פאות הקובייה בשחור ולבן, ואז לגלגל את הקובייה על פני הלוח כך שכל פעם הפאה שנוגעת בלוח תהיה באותו הצבע כמו המשבצת בה היא נוגעת. הקובייה אמורה לעבור בכל משבצת בלוח בדיוק פעם אחת. האם שלומי יוכל לעשות זאת? נמקו או הביאו דוגמה.

נושאים:
קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון הוכחה ודוגמה -> הוכחה בשלילה קומבינטוריקה -> צביעות -> צביעת שחמט

הפרשים בלוח הכפל

צובעים את לוח הכפל `10xx10` בצביעת שחמט שחור ולבן, כך שהמשבצת של `1xx1` צבועה בשחור.
מצאו את ההפרש בין סכום כל המספרים במשבצות השחורות לסכום כל המספרים במשבצות הלבנות.

	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

אריתמטיקה קומבינטוריקה -> טבלאות מספריות קומבינטוריקה -> צביעות -> צביעת שחמט

מקורות:

	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100