קומבינטוריקה, גאומטריה קומבינטורית, חתכו צורה

בעיות חיתוך ופירוק צורות כוללות חיתוך צורה גאומטרית נתונה לחלקים שניתן לסדר מחדש ליצירת צורה אחרת מוגדרת, או כדי לעמוד בתנאים מסוימים (למשל, יצירת חלקים זהים). שאלות בודקות חשיבה מרחבית והבנה של שימור שטח.

  • פאזל גזירה

    הנה חידה קטנה בגזירה. אני לוקח רצועת נייר, בגודל חמישה אינץ' על אינץ' אחד, ובאמצעות חיתוך לחמישה חלקים, החלקים מתאימים יחד ויוצרים ריבוע, כפי שמוצג באיור. עכשיו, זהו פאזל די מעניין לגלות איך אנחנו יכולים לעשות זאת רק בארבעה חלקים.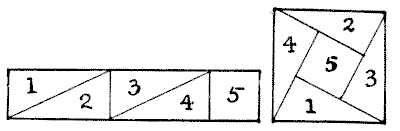 מקורות:

  • שטיח האח של גברת הובסון

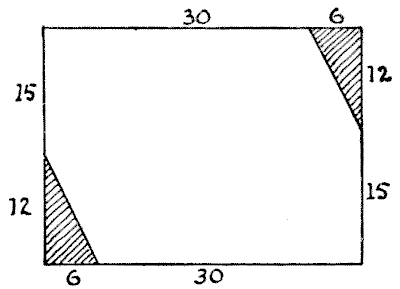
    לבנה של גברת הובסון הייתה תאונה כששיחק באש, ושרף שתיים מפינותיו של שטיח אח יפה. הפינות הפגומות נחתכו, וכעת יש לו את המראה והפרופורציות המוצגים בדיאגרמה שלי. איך גברת הובסון צריכה לחתוך את השטיח למספר המינימלי האפשרי של חלקים שיתאימו זה לזה וייצרו שטיח מרובע לחלוטין? ניתן לראות שהשטיח הוא בפרופורציות של `36` × `27` (לא משנה אם נאמר אינצ'ים או יארדים), וכל חתיכה שנחתכה הייתה במידות של `12` ו-`6` מבחוץ כמו בציור.

    מקורות:

  • המחומש והריבוע

    מעניין אותי כמה מקוראיי, מבין אלה שלא הקדישו תשומת לב רבה ליסודות הגיאומטריה, יוכלו לצייר מחומש משוכלל, או צורה בעלת חמש צלעות, אם יידרשו לעשות זאת באופן פתאומי. משושה משוכלל, או צורה בעלת שש צלעות, הוא די קל, כי כולם יודעים שכל מה שצריך לעשות הוא לתאר מעגל ואז, לקחת את הרדיוס כאורך אחת הצלעות, ולסמן את שש הנקודות סביב ההיקף. אבל מחומש הוא עניין אחר לגמרי. אז, מכיוון שהחידה שלי קשורה לחיתוך של מחומש משוכלל, אולי כדאי שאקודם כל אראה לקוראים הפחות מנוסים שלי איך יש לצייר צורה זו בצורה נכונה. תארו מעגל וציירו את שני הקווים H B ו-D G, בתרשים, דרך המרכז בזוויות ישרות. כעת מצאו את הנקודה A, באמצע בין C ו-B. לאחר מכן הניחו את חוד המצפן שלכם ב-A ועם המרחק A D תארו את הקשת החותכת את H B ב-E. לאחר מכן הניחו את חוד המצפן שלכם ב-D ועם המרחק D E תארו את הקשת החותכת את ההיקף ב-F. כעת, D F היא אחת הצלעות של המחומש שלכם, ועליכם פשוט לסמן את הצלעות האחרות סביב המעגל. די פשוט כשאתם יודעים איך, אבל אחרת קצת קשה.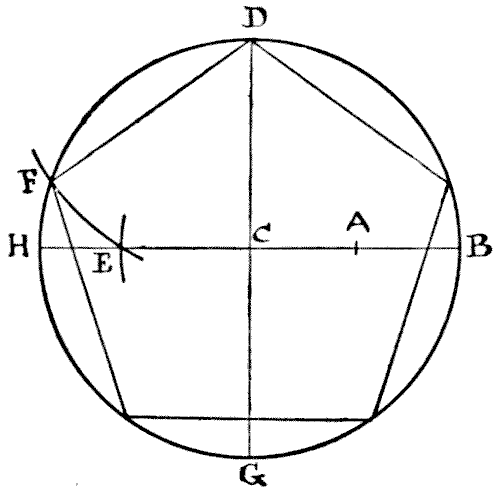 לאחר שיצרתם את המחומש שלכם, החידה היא לחתוך אותו למספר המועט ביותר של חלקים שיתאימו זה לזה וייצרו ריבוע מושלם. מקורות:

  • המשולש המנותח

     

    חידה טובה היא זו שהג'נטלמן באיור מציג לחבריו. הוא פשוט גזר מנייר משולש שווה צלעות — כלומר, משולש שבו שלוש הצלעות באותו אורך. הוא מציע לחתוך אותו לחמישה חלקים בצורה כזו שהם יתאימו זה לזה וייצרו שניים או שלושה משולשים שווי צלעות קטנים יותר, תוך שימוש בכל החומר בכל מקרה. האם תוכלו לגלות כיצד יש לבצע את החיתוכים?

    זכרו שכאשר הכנתם את חמשת החלקים שלכם, עליכם להיות מסוגלים, כרצוי, לחבר אותם יחד כדי ליצור או את המשולש המקורי הבודד או ליצור שני משולשים או ליצור שלושה משולשים — כולם שווי צלעות.

    מקורות:

  • השולחן והשרפרפים

    הזדמן לי לא פעם להראות שהתשובות שפורסמו למספר רב של החידות העתיקות והידועות ביותר הן שגויות לחלוטין או ניתנות לשיפור. אני מציע לשקול את החידה הישנה של השולחן והשרפרפים שרוב הקוראים שלי ראו כנראה בצורה זו או אחרת בספרים שנערכו לשעשוע הילדות.

    הסיפור מספר שמנהל בית ספר חסכן ובעל תושייה רצה פעם להפוך משטח שולחן עגול, שלא היה לו שימוש בו, למושבים עבור שני שרפרפים אובליים, שלכל אחד מהם חור אחיזה במרכז. הוא הורה לנגר לבצע את החיתוכים כפי שמוצג באיור ולאחר מכן לחבר את שמונת החלקים יחד באופן המוצג. הוא התרשם כל כך מהתושייה שבהופעתו, שהוא הציג את החידה לכיתת הגיאומטריה שלו כלימוד קטן בניתוח. אבל המשך הסיפור מעולם לא פורסם, מכיוון שלפי השמועה, היה זה אופייני למנהלי האקדמיות שהם לעולם לא יודו שהם יכולים לטעות. אני מקבל את המידע שלי מצאצא של הילד המקורי שהיה לו הכי הרבה סיבות להתעניין בעניין.

    הצעיר החכם הציע בענווה למורה שחורי האחיזה גדולים מדי, וייתכן שילד קטן עלול ליפול דרכם. לכן הוא הציע דרך נוספת לבצע את החיתוכים שתתגבר על ההתנגדות הזו. על חוצפתו הוא קיבל עונש כה חמור שהוא השתכנע שככל שחור האחיזה בשרפרפים גדול יותר, כך הם עלולים להיות נוחים יותר. 

     

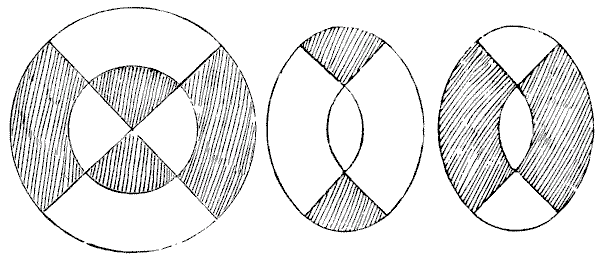
    מה הייתה השיטה שהילד הציע?

    האם אתה יכול להראות כיצד ניתן לחתוך את משטח השולחן העגול לשמונה חלקים שיתאימו זה לזה וייצרו שני מושבים אובליים לשרפרפים (כל אחד באותו גודל וצורה בדיוק) ולכל אחד מהם חורי אחיזה דומים במידות קטנות יותר מאשר במקרה המוצג לעיל? כמובן, יש להשתמש בכל העץ.

    מקורות:

  • המונד הגדול

     

    הנה סמל בעל עתיקות עצומה הראוי לתשומת לב. הוא מוטבע על נס קוריאה ועל דגל הסוחר שלה, ואומץ כסימן מסחרי על ידי חברת הרכבות Northern Pacific, אם כי מעטים מודעים לכך שמדובר במונד הגדול, כפי שמוצג בסקיצה למטה. סימן זה עבור הסיני הוא כמו הצלב עבור הנוצרי. זהו סימן האלוהות והנצח, בעוד שני החלקים שאליהם מחולק המעגל נקראים יין ויאנג—הכוחות הזכריים והנקביים של הטבע. סופר בנושא לפני יותר משלושת אלפים שנה דיווח כי אמר בהתייחסו אליו: "הבלתי מוגבל מייצר את הקיצוניות הגדולה. הקיצוניות הגדולה מייצרת את שני העקרונות. שני העקרונות מייצרים את ארבעת הרבעים, ומארבעת הרבעים אנו מפתחים את הריבוע של שמונת הדיאגרמות של פואה-הי." אני מקווה שהקוראים לא יבקשו ממני להסביר זאת, כי אין לי מושג קלוש מה זה אומר. עם זאת, אני משוכנע שבמשך עידנים לסמל היו משמעויות נסתרות וכנראה מתמטיות עבור הסטודנט האזוטרי.

    אציג את המונד בצורתו היסודית. הנה שלוש שאלות קלות בנוגע לסמל הגדול הזה:—

    (I.) למי יש שטח גדול יותר, למעגל הפנימי המכיל את היין והיאנג, או לטבעת החיצונית?

    (II.) חלקו את היין והיאנג לארבעה חלקים באותו גודל ובאותה צורה על ידי חתך אחד.

    (III.) חלקו את היין והיאנג לארבעה חלקים באותו גודל, אך בצורה שונה, על ידי חתך ישר אחד.

    מקורות:

  • שני פרסות הסוס

    מדוע יש להתייחס לפרסות סוס כאל "מזל" הוא אחד מאותם דברים שאף אדם לא יכול להבין. זוהי אמונה טפלה עתיקה מאוד, וג'ון אוברי (`1626-1700`) אומר, "לרוב הבתים בווסט אנד של לונדון יש פרסת סוס על סף הדלת." ברחוב מונמות' היו שבע עשרה בשנת `1813` ושבע עד לשנת `1855`. אפילו לורד נלסון מסמר אחת לתורן של הספינה ויקטורי. כיום אנו מוצאים שזה יותר מועיל ל"מזל טוב" לוודא שהם ממוסמרים היטב על רגלי הסוס שאנו עומדים לנסוע בו.

    אף על פי כן, עד כמה שהפרסה, כמו הצלב קרס וסמלים אחרים שיצא לי לעסוק בהם מדי פעם, שימשה לסמל בריאות, שגשוג ורצון טוב כלפי בני אדם, אנו יכולים להתייחס אליה בכבוד מסוים. האם ייתכן שיש איזשהו מסתורין מתמטי איזוטרי או אבוד החבוי בצורת פרסת סוס? בחנתי את הנושא הזה, ואני רוצה להסב את תשומת לבם של הקוראים שלי לעובדה המדהימה ביותר שזוג פרסות הסוס המוצגות באיור שלי קשורות בצורה בולטת ויפה לעיגול, שהוא הסמל של הנצח. אני מציג את העובדה הזו בצורה של בעיה פשוטה, כדי שניתן יהיה לראות עד כמה הקשר הזה הוסתר בצורה מתוחכמת במשך עידנים רבים. הקוראים שלי ישמחו, אני יודע, כשהם ימצאו את המפתח למסתורין.

     

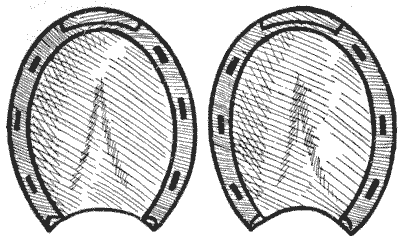
    גזרו בזהירות את שתי פרסות הסוס מסביב לקו המתאר ואז חתכו אותן לארבעה חלקים, שכולם שונים בצורתם, שיתאימו זה לזה וייצרו מעגל מושלם. כל נעל חייבת להיחתך לשני חלקים וכל החלק בטלף הסוס הכלול בתוך קו המתאר ישמש וייחשב כחלק מהשטח.

    מקורות:

  • חידת בטסי רוס

    כתב לי כתב וביקש ממני לספק לו את הפתרון לחידה ישנה המיוחסת לבטסי רוס מפילדלפיה, שהראתה אותה לג'ורג' וושינגטון. היא מורכבת מקיפול פיסת נייר כך שבעזרת גזירה אחת במספריים ניתן יהיה ליצור כוכב חמש-קצוות של חופש. אני לא יכול לומר אם סיפור מקור החידה הוא אמיתי או לא, אבל יש לי הדפס של הבית הישן בפילדלפיה שבו נאמר שהגברת גרה, ואני מאמין שהוא עדיין עומד שם. אבל הקוראים שלי ללא ספק יתעניינו בחידה הקטנה הזו.

    קחו פיסת נייר עגולה וקפלו אותה כך שבעזרת חיתוך אחד במספריים תוכלו ליצור כוכב מושלם בעל חמש פינות.

    מקורות:

  • שרשרת הקרטון

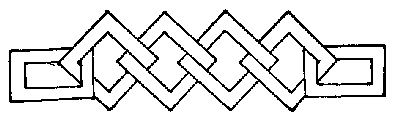    האם תוכלו לגזור את השרשרת הזו מחתיכת קרטון ללא כל חיבור שהוא? כל חוליה היא מוצקה; מבלי שנחתכה וחובּרה מחדש בשום מקום. זהו חידה ישנה ומעניינת שלמדתי כשהייתי ילד, אך אין לי ידע לגבי ממציאה. מקורות:

  • חידת תפוח האדמה

    קחו פרוסה עגולה של תפוח אדמה, הניחו אותה על השולחן, ובדקו לכמה חלקים תוכלו לחלק אותה באמצעות שישה חיתוכים בסכין. כמובן שאסור לכם לסדר מחדש את החלקים או לערום אותם לאחר חיתוך. מהו המספר הגדול ביותר של חלקים שתוכלו ליצור?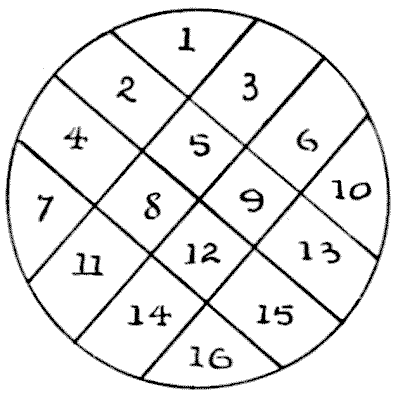 האיור מראה כיצד ליצור שישה עשר חלקים. כמובן שאפשר לשפר תוצאה זו בקלות. מקורות: