קומבינטוריקה, גאומטריה קומבינטורית, חתכו צורה

בעיות חיתוך ופירוק צורות כוללות חיתוך צורה גאומטרית נתונה לחלקים שניתן לסדר מחדש ליצירת צורה אחרת מוגדרת, או כדי לעמוד בתנאים מסוימים (למשל, יצירת חלקים זהים). שאלות בודקות חשיבה מרחבית והבנה של שימור שטח.

• חיתוך לינולאום

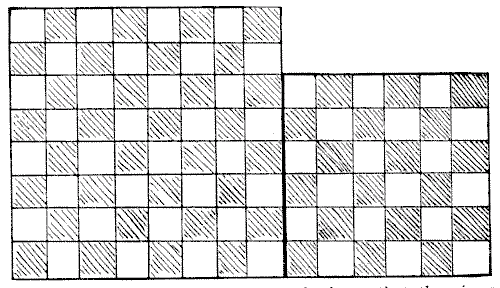  הדיאגרמה כאן מייצגת שני חלקי לינולאום נפרדים. דוגמת המשבצות לא חוזרת על עצמה בגב, כך שלא ניתן להפוך את החלקים. החידה היא לחתוך את שתי הריבועים לארבעה חלקים כך שהם יתאימו זה לזה וייצרו ריבוע מושלם אחד בגודל `10`×`10`, כך שהדוגמה תתאים כראוי, וכך שלחלק הגדול יותר יהיה חלק קטן ככל האפשר שנחתך ממנו.
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 176

• חידת לינולאום נוספת

   

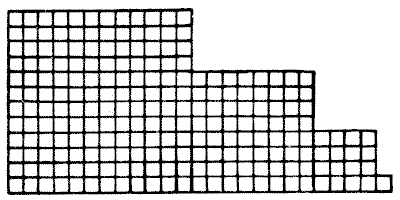
  האם תוכלו לחתוך את פיסת הלינולאום הזו לארבע חתיכות שיתאימו זו לזו וייצרו ריבוע מושלם? כמובן שהחיתוכים יכולים להתבצע רק לאורך הקווים.

  נושאים:

  גאומטריה -> גאומטריה במישור קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 177

• ארבעת הבנים

  קוראים יזהו את הדיאגרמה כחבר ותיק מימי נעוריהם. לאיש הייתה אחוזה בצורת ריבוע. הוא הוריש לאלמנתו את הרבע המוצל של האחוזה. את היתר היה צריך לחלק באופן שווה בין ארבעת בניו, כך שכל אחד יקבל קרקע באותו שטח בדיוק ובאותה צורה בדיוק. מוצג לנו איך זה נעשה. אבל המשך הסיפור אינו ידוע כל כך. במרכז האחוזה הייתה באר, המסומנת על ידי הנקודה הכהה, ובנימין, צ'ארלס ודוד התלוננו שהחלוקה אינה "הוגנת", מכיוון שלאAlfred הייתה גישה לבאר הזו, בעוד שהם לא יכלו להגיע אליה מבלי להסיג את גבולו של מישהו אחר. החידה היא להראות כיצד יש לחלק את האחוזה כך שלכל בן תהיה קרקע באותו צורה ובאותו שטח, ולכל אחד תהיה גישה לבאר מבלי לרדת מהשטח שלו.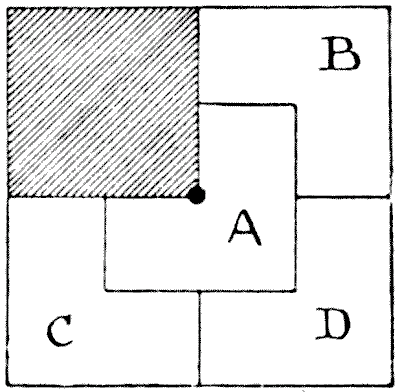
  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 180

• חומות הגן

   

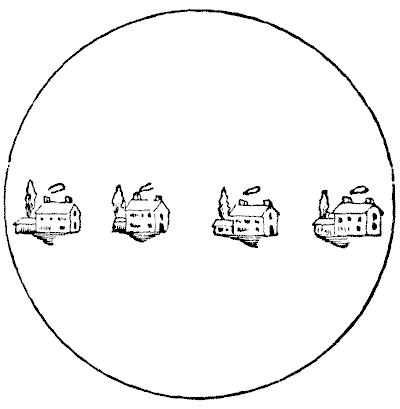
  יזם נדל"ן ספקולטיבי מחזיק בשדה עגול, עליו הקים ארבעה קוטג'ים, כפי שמוצג באיור. השדה מוקף בחומה מלבנים, והבעלים התחייב להקים עוד שלושה קירות לבנים, כך שהשכנים לא יוכלו להציץ אחד לשני, אך ארבעת הדיירים מתעקשים שלא תהיה אפליה, ושלכל אחד יהיה בדיוק אותו אורך שטח קיר לעצי הפרי שלו. החידה היא להראות כיצד ניתן לבנות את שלושת הקירות כך שלכל דייר יהיה אותו שטח אדמה, ובדיוק אותו אורך של קיר.

  כמובן, כל גן חייב להיות סגור לחלוטין על ידי קירותיו, וחייב להיות אפשרי להוכיח שלכל גן יש בדיוק אותו אורך של קיר. אם החידה נפתרת כראוי, אין צורך במספרים.

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 194

• חידת גפרורים חדשה

  באיור מוצגים שמונה-עשר גפרורים המסודרים כך שהם תוחמים שני שטחים, כאשר אחד גדול פי שניים מהשני. האם תוכלו לסדר אותם מחדש (`1`) כך שיתחמו שני שטחים מרובעים, כאשר אחד גדול בדיוק פי שלושה מהשני, ו- (`2`) כך שיתחמו שני שטחים מחומשים, כאשר אחד גדול בדיוק פי שלושה מהשני? יש להשתמש בכל שמונה-עשר הגפרורים בצורה הוגנת בכל מקרה; שני השטחים חייבים להיות מופרדים לחלוטין, ולא צריכים להיות קצוות רופפים או גפרורים כפולים.
  נושאים:

  גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה חידות ורבוסים -> חידות גפרורים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 204

• מטע בבורמה

  לפני זמן קצר קיבלתי מכתב מעניין מהכומר הבריטי במייקטילה, בורמה העליונה, בו כתב לי הכומר שנהנה באונייה בדרכו לשם לנסות לפתור את החידה הקטנה הזו.

   

  אם יש לו מטע של ארבעים ותשעה עצים, נטועים בצורת ריבוע כפי שמוצג באיור המצורף, הוא רוצה לדעת איך הוא יכול לכרות עשרים ושבעה מהעצים כך שעשרים ושניים העצים שיישארו יעמדו בשורות רבות ככל האפשר עם ארבעה עצים בכל שורה.

  כמובן שלא יכולים להיות יותר מארבעה עצים בשורה.

  נושאים:

  קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 212

• חלוקות לוח שחמט

  לאחרונה שאלתי את עצמי את השאלה: בכמה דרכים שונות ניתן לחלק לוח שחמט לשני חלקים באותו גודל וצורה על ידי חתכים לאורך הקווים המחלקים את הריבועים? עד מהרה התברר שהבעיה מרתקת ומלאת קשיים. אני מציג אותה בצורה פשוטה, תוך שימוש בלוח בעל ממדים קטנים יותר. ברור שלוח של ארבעה ריבועים יכול להיות מחולק רק בדרך אחת - על ידי חיתוך ישר במרכז - מכיוון שלא נספור היפוכים ושיקופים כשונים. במקרה של לוח של שישה עשר ריבועים - ארבעה על ארבעה - יש בדיוק שש דרכים שונות. נתתי את כולן בתרשים, והקורא לא ימצא אחרות. כעת, קחו את הלוח הגדול יותר של שלושים ושישה ריבועים, ונסו לגלות בכמה דרכים ניתן לחתוך אותו לשני חלקים באותו גודל וצורה.
  נושאים:

  קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 288

• אריות וכתרים

  הגברת הצעירה באיור מתמודדת עם קושי קטן בגזירה, שבו הקורא ישמח לסייע לה. היא רוצה, מסיבה כלשהי שהיא לא מסרה לי, לחתוך את חתיכת הבד המרובעת והיקרה הזו לארבעה חלקים, כולם בדיוק באותו גודל ובאותה צורה, אבל חשוב שכל חתיכה תכיל אריה וכתר. מכיוון שהיא מתעקשת שהחתכים ייעשו רק לאורך הקווים המחלקים את הריבועים, היא נבוכה למדי לגלות איך לעשות זאת. האם תוכלו להראות לה את הדרך? יש רק שיטה אפשרית אחת לחתוך את הבד.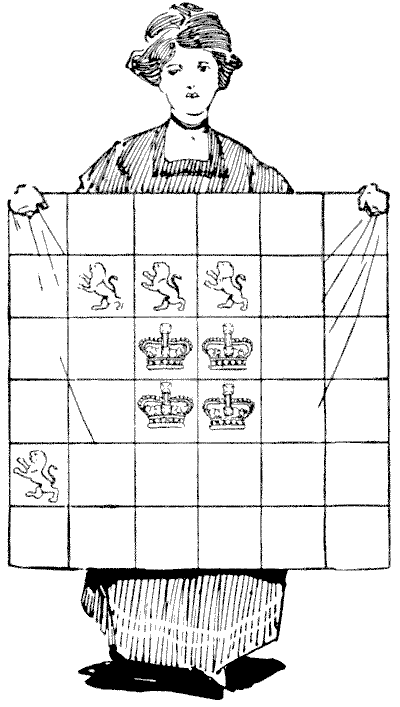
  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 289

• לוחות עם מספר אי-זוגי של משבצות

  אנו נדון כאן בשאלה של אותם לוחות המכילים מספר אי-זוגי של משבצות. נניח שהמשבצת המרכזית נחתכת תחילה, כך שיישאר מספר זוגי של משבצות לחלוקה. כעת, ברור שלוח ריבוע שלוש על שלוש ניתן לחלוקה רק בדרך אחת, כפי שמוצג באיור `1`. ניתן לראות שהחלקים A ו-B הם באותו גודל וצורה, וכי כל דרך חיתוך אחרת תייצר רק חלקים בעלי צורה זהה, אז זכרו שווריאציות אלה אינן נספרות כדרכים שונות. החידה שאני מציע היא לחתוך את הלוח חמש על חמש (איור `2`) לשני חלקים באותו גודל וצורה בכמה שיותר דרכים שונות. הדגמתי באיור דרך אחת לעשות זאת. כמה דרכים שונות יש בסך הכל? חתיכה שכאשר הופכים אותה דומה לחתיכה אחרת אינה נחשבת כבעלת צורה שונה.
  נושאים:

  גאומטריה -> גאומטריה במישור -> סימטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 290

• הבעיה של הגראנד לאמה

  לפני זמן רב היה גראנד לאמה שהייתה לו לוח שחמט עשוי זהב טהור, חרוט בצורה מפוארת, וכמובן, בעל ערך רב. מדי שנה נערך טורניר בלהסה בין הכמרים, ובכל פעם שמישהו ניצח את הגראנד לאמה זה נחשב לכבוד גדול, ושמו נכתב על גב הלוח, ותכשיט יקר הוצב במשבצת המסוימת שבה ניתן השחמט. לאחר שהפונטיף הריבוני הזה הובס בארבעה מקרים הוא מת - אולי מצער.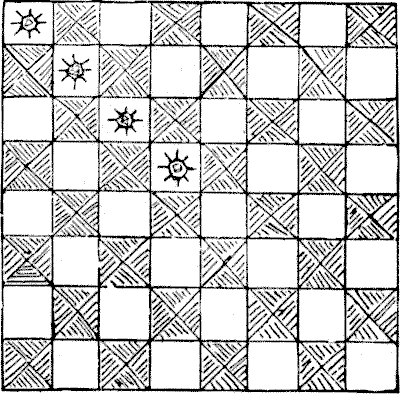 כעת הגראנד לאמה החדש היה שחקן שחמט נחות, והעדיף צורות אחרות של שעשוע תמים, כמו עריפת ראשים של אנשים. אז הוא פסל את השחמט כמשחק משפיל, שלא שיפר לא את המוח ולא את המוסר, וביטל את הטורניר באופן מיידי. ואז הוא שלח לארבעת הכמרים שהייתה להם החוצפה לשחק טוב יותר מגראנד לאמה, ופנה אליהם כדלקמן: "אנשים עלובים וכופרים, המכנים את עצמכם כמרים! האם אינכם יודעים שלטעון ליכולת לעשות משהו טוב יותר מקודמי הוא עבירה שעונשה מוות? קחו את לוח השחמט הזה ולפני שהשחר יעלה על חדר העינויים, חתכו אותו לארבעה חלקים שווים בעלי אותו צורה, שכל אחד מהם מכיל שישה עשר ריבועים מושלמים, עם אחד מהאבנים היקרות בכל חלק! אם תיכשלו בכך, אז יומצאו ספורט אחרים להנאתכם המיוחדת. לכו!" ארבעת הכמרים הצליחו במשימתם שנראתה חסרת סיכוי. האם תוכלו להראות כיצד ניתן לחלק את הלוח לארבעה חלקים שווים, שכל אחד מהם בעל אותו צורה בדיוק, על ידי חיתוכים לאורך הקווים המחלקים את הריבועים, כאשר כל חלק מכיל אחת מהאבנים היקרות?
  נושאים:

  קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה חידות ורבוסים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 291