几何学, 平面几何学, 平面变换, 全等变换(等距变换)
等距变换是保持距离和角度度量不变的变换,意味着变换后的图形(像)与原始图形全等。这些包括平移、旋转和反射。问题侧重于应用这些变换并理解它们的属性。
平行平移/平移 旋转 反射-
分割成四个相等的部分
如果几何形状在彼此叠放时重合,则称它们全等。将下面的形状切割成四个全等的部分:
来源: -
问题
在平面上,给定 `12` 条相交的直线。证明其中必有两条直线之间的夹角小于 `17^@`。
-
在线条上的三角形
六个全等的等腰三角形如图所示放置在一起。
证明点 C、F 和 M 在一条直线上。 来源:
来源: -
五边形
在凸五边形 `ABCDE` 中,已知: `AE=AD`, `AB=AC` 且 `angle CAD=angle ABE + angle AEB`。
在三角形 `ABE` 中,作中线 `AM`。 证明: `AM` 的长度是线段 `CD` 长度的一半。
来源: -
问题
在边长为 1 的正方形 ABCD 内标记一点 E,在正方形外标记一点 F,使得三角形 ABE 和 DAF 均为等边三角形。计算五边形 CBEFD 的面积。
来源:

-
问题
有一个台球桌,其形状为三角形,其角分别为\(90^{\circ}\)、\(30^{\circ}\)和\(60^{\circ}\)。
给定一个直角三角形的台球桌,其角上有“袋”。 其中一个锐角为\(30^{\circ}\)。 从这个角(30 度角)发出的球击中三角形的对边中点(中线)。 证明,如果球被反弹超过八次(入射角等于反射角),那么最终球将进入位于三角形 60 度角的“袋”中。
-
问题
将给定的形状切割成四个全等的部分:
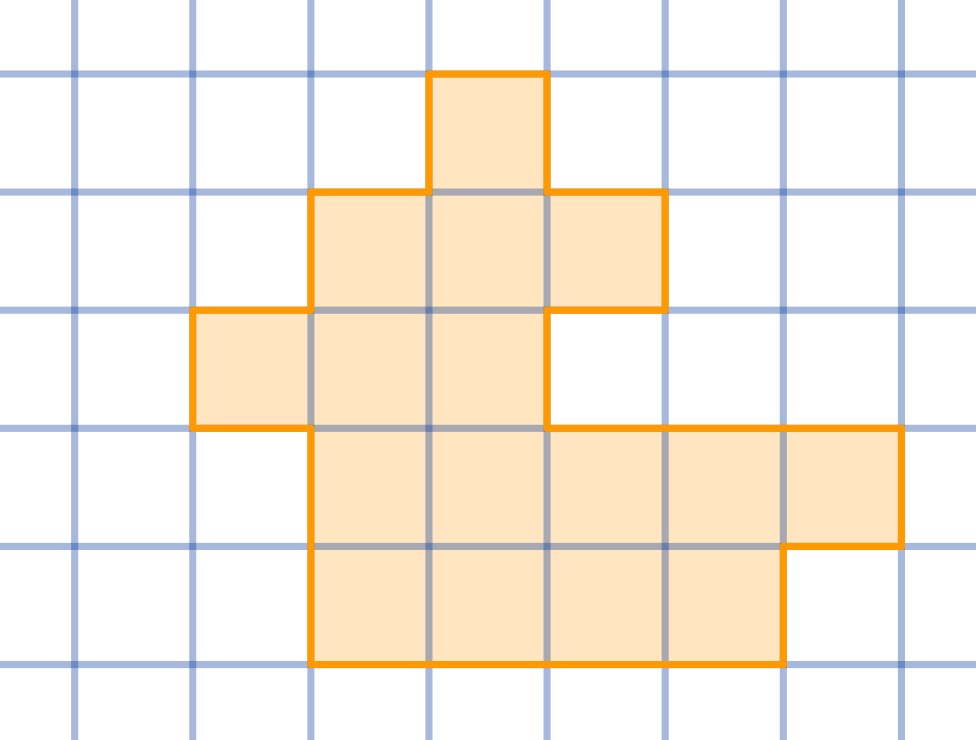
-
平面上的旅行
给定一个平面直角坐标系 x-y。需要从点 (1,0) 到达点 (2006,2005),每次移动可以向上(沿 y 轴正方向)移动一个单位,或者向右(沿 x 轴正方向)移动一个单位。
a. 有多少种不同的路径可以完成这个任务?
b. 如果不允许在任何阶段通过位于直线 x=y 上的点,那么有多少种不同的路径可以完成这个任务?
来源:
