Combinatorics

Combinatorics is the art of counting. It deals with selections, arrangements, and combinations of objects. Questions involve determining the number of ways to perform tasks, arrange items (permutations), or choose subsets (combinations), often using principles like the product rule and sum rule.

Pigeonhole Principle Double Counting Binomial Coefficients and Pascal's Triangle Product Rule / Rule of Product Graph Theory Matchings Induction (Mathematical Induction) Game Theory Combinatorial Geometry Invariants Case Analysis / Checking Cases Processes / Procedures Number Tables Colorings

  • MRS. HOBSON'S HEARTHRUG

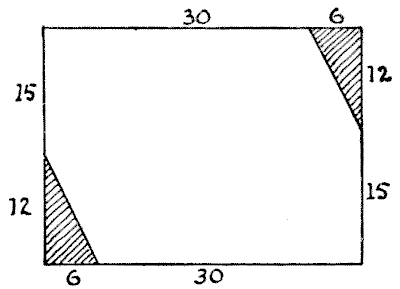
    Mrs. Hobson's boy had an accident when playing with the fire, and burnt two of the corners of a pretty hearthrug. The damaged corners have been cut away, and it now has the appearance and proportions shown in my diagram. How is Mrs. Hobson to cut the rug into the fewest possible pieces that will fit together and form a perfectly square rug? It will be seen that the rug is in the proportions `36` × `27` (it does not matter whether we say inches or yards), and each piece cut away measured `12` and `6` on the outside.

    Sources:

  • THE PENTAGON AND SQUARE

    I wonder how many of my readers, amongst those who have not given any close attention to the elements of geometry, could draw a regular pentagon, or five-sided figure, if they suddenly required to do so. A regular hexagon, or six-sided figure, is easy enough, for everybody knows that all you have to do is to describe a circle and then, taking the radius as the length of one of the sides, mark off the six points round the circumference. But a pentagon is quite another matter. So, as my puzzle has to do with the cutting up of a regular pentagon, it will perhaps be well if I first show my less experienced readers how this figure is to be correctly drawn. Describe a circle and draw the two lines H B and D G, in the diagram, through the centre at right angles. Now find the point A, midway between C and B. Next place the point of your compasses at A and with the distance A D describe the arc cutting H B at E. Then place the point of your compasses at D and with the distance D E describe the arc cutting the circumference at F. Now, D F is one of the sides of your pentagon, and you have simply to mark off the other sides round the circle. Quite simple when you know how, but otherwise somewhat of a poser.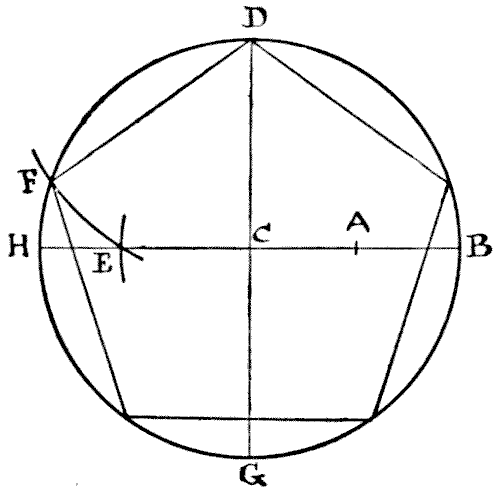 Having formed your pentagon, the puzzle is to cut it into the fewest possible pieces that will fit together and form a perfect square. Sources:

  • THE DISSECTED TRIANGLE

     

    A good puzzle is that which the gentleman in the illustration is showing to his friends. He has simply cut out of paper an equilateral triangle—that is, a triangle with all its three sides of the same length. He proposes that it shall be cut into five pieces in such a way that they will fit together and form either two or three smaller equilateral triangles, using all the material in each case. Can you discover how the cuts should be made?

    Remember that when you have made your five pieces, you must be able, as desired, to put them together to form either the single original triangle or to form two triangles or to form three triangles—all equilateral.

    Sources:

  • THE TABLE-TOP AND STOOLS

    I have frequently had occasion to show that the published answers to a great many of the oldest and most widely known puzzles are either quite incorrect or capable of improvement. I propose to consider the old poser of the table-top and stools that most of my readers have probably seen in some form or another in books compiled for the recreation of childhood.

    The story is told that an economical and ingenious schoolmaster once wished to convert a circular table-top, for which he had no use, into seats for two oval stools, each with a hand-hole in the centre. He instructed the carpenter to make the cuts as in the illustration and then join the eight pieces together in the manner shown. So impressed was he with the ingenuity of his performance that he set the puzzle to his geometry class as a little study in dissection. But the remainder of the story has never been published, because, so it is said, it was a characteristic of the principals of academies that they would never admit that they could err. I get my information from a descendant of the original boy who had most reason to be interested in the matter.

    The clever youth suggested modestly to the master that the hand-holes were too big, and that a small boy might perhaps fall through them. He therefore proposed another way of making the cuts that would get over this objection. For his impertinence he received such severe chastisement that he became convinced that the larger the hand-hole in the stools the more comfortable might they be. 

     

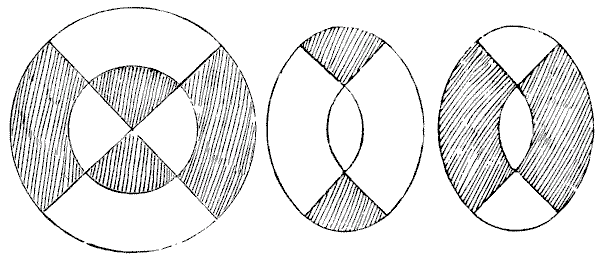
    Now what was the method the boy proposed?

    Can you show how the circular table-top may be cut into eight pieces that will fit together and form two oval seats for stools (each of exactly the same size and shape) and each having similar hand-holes of smaller dimensions than in the case shown above? Of course, all the wood must be used.

    Sources:

  • THE GREAT MONAD

     

    Here is a symbol of tremendous antiquity which is worthy of notice. It is borne on the Korean ensign and merchant flag, and has been adopted as a trade sign by the Northern Pacific Railroad Company, though probably few are aware that it is the Great Monad, as shown in the sketch below. This sign is to the Chinaman what the cross is to the Christian. It is the sign of Deity and eternity, while the two parts into which the circle is divided are called the Yin and the Yan—the male and female forces of nature. A writer on the subject more than three thousand years ago is reported to have said in reference to it: "The illimitable produces the great extreme. The great extreme produces the two principles. The two principles produce the four quarters, and from the four quarters we develop the quadrature of the eight diagrams of Feuh-hi." I hope readers will not ask me to explain this, for I have not the slightest idea what it means. Yet I am persuaded that for ages the symbol has had occult and probably mathematical meanings for the esoteric student.

    I will introduce the Monad in its elementary form. Here are three easy questions respecting this great symbol:—

    (I.) Which has the greater area, the inner circle containing the Yin and the Yan, or the outer ring?

    (II.) Divide the Yin and the Yan into four pieces of the same size and shape by one cut.

    (III.) Divide the Yin and the Yan into four pieces of the same size, but different shape, by one straight cut.

    Sources:

  • THE TWO HORSESHOES

    Why horseshoes should be considered "lucky" is one of those things which no man can understand. It is a very old superstition, and John Aubrey (`1626-1700`) says, "Most houses at the West End of London have a horseshoe on the threshold." In Monmouth Street there were seventeen in `1813` and seven so late as `1855`. Even Lord Nelson had one nailed to the mast of the ship Victory. To-day we find it more conducive to "good luck" to see that they are securely nailed on the feet of the horse we are about to drive.

    Nevertheless, so far as the horseshoe, like the Swastika and other emblems that I have had occasion at times to deal with, has served to symbolize health, prosperity, and goodwill towards men, we may well treat it with a certain amount of respectful interest. May there not, moreover, be some esoteric or lost mathematical mystery concealed in the form of a horseshoe? I have been looking into this matter, and I wish to draw my readers' attention to the very remarkable fact that the pair of horseshoes shown in my illustration are related in a striking and beautiful manner to the circle, which is the symbol of eternity. I present this fact in the form of a simple problem, so that it may be seen how subtly this relation has been concealed for ages and ages. My readers will, I know, be pleased when they find the key to the mystery.

     

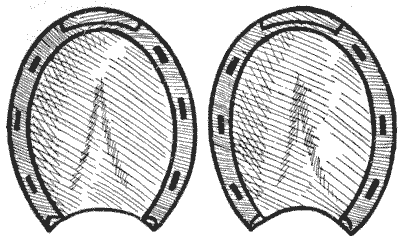
    Cut out the two horseshoes carefully round the outline and then cut them into four pieces, all different in shape, that will fit together and form a perfect circle. Each shoe must be cut into two pieces and all the part of the horse's hoof contained within the outline is to be used and regarded as part of the area.

    Sources:

  • THE BETSY ROSS PUZZLE

    A correspondent asked me to supply him with the solution to an old puzzle that is attributed to a certain Betsy Ross, of Philadelphia, who showed it to George Washington. It consists in so folding a piece of paper that with one clip of the scissors a five-pointed star of Freedom may be produced. Whether the story of the puzzle's origin is a true one or not I cannot say, but I have a print of the old house in Philadelphia where the lady is said to have lived, and I believe it still stands there. But my readers will doubtless be interested in the little poser.

    Take a circular piece of paper and so fold it that with one cut of the scissors you can produce a perfect five-pointed star.

    Sources:

  • THE CARDBOARD CHAIN

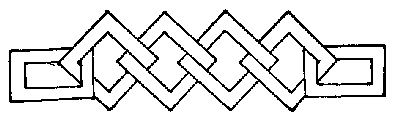    Can you cut this chain out of a piece of cardboard without any join whatever? Every link is solid; without its having been split and afterwards joined at any place. It is an interesting old puzzle that I learnt as a child, but I have no knowledge as to its inventor. Sources:

  • THE POTATO PUZZLE

    Take a circular slice of potato, place it on the table, and see into how large a number of pieces you can divide it with six cuts of a knife. Of course you must not readjust the pieces or pile them after a cut. What is the greatest number of pieces you can make? The illustration shows how to make sixteen pieces. This can, of course, be easily beaten. Sources:

  • THE SEVEN PIGS

     

    Here is a little puzzle that was put to one of the sons of Erin the other day and perplexed him unduly, for it is really quite easy. It will be seen from the illustration that he was shown a sketch of a square pen containing seven pigs. He was asked how he would intersect the pen with three straight fences so as to enclose every pig in a separate sty. In other words, all you have to do is to take your pencil and, with three straight strokes across the square, enclose each pig separately. Nothing could be simpler.

    The Irishman complained that the pigs would not keep still while he was putting up the fences. He said that they would all flock together, or one obstinate beast would go into a corner and flock all by himself. It was pointed out to him that for the purposes of the puzzle the pigs were stationary. He answered that Irish pigs are not stationery—they are pork. Being persuaded to make the attempt, he drew three lines, one of which cut through a pig. When it was explained that this is not allowed, he protested that a pig was no use until you cut its throat. "Begorra, if it's bacon ye want without cutting your pig, it will be all gammon." We will not do the Irishman the injustice of suggesting that the miserable pun was intentional. However, he failed to solve the puzzle. Can you do it?

    Sources: