שעשועונים במתמטיקה, הנרי ארנסט דודני
-
שאלה 171 - חידת הבאנר
 לגברת הייתה חתיכת בד מרובעת עם שני אריות עליה, שהאיור הוא שעתוק מוקטן ומדויק שלה. היא רצתה לחתוך את הבד לחתיכות שיתאימו זו לזו וייצרו שני באנרים מרובעים עם אריה על כל באנר. היא גילתה שאפשר לעשות זאת בארבע חתיכות בלבד. איך היא הצליחה? כמובן, לחתוך את האריה הבריטי יהיה פשע בל יכופר, אז עליכם להיזהר שאף חיתוך לא יעבור דרך אף חלק מהם. לגברות נמסר שאין להתחשב כלל ב"תפרים", ואין לבזבז אף חלק מהחומר. זוהי חידת חיתוך פשוטה למדי אם ניגשים אליה נכון. זכרו שהבאנרים צריכים להיות ריבועים מושלמים, אם כי הם לא צריכים להיות באותו גודל.
לגברת הייתה חתיכת בד מרובעת עם שני אריות עליה, שהאיור הוא שעתוק מוקטן ומדויק שלה. היא רצתה לחתוך את הבד לחתיכות שיתאימו זו לזו וייצרו שני באנרים מרובעים עם אריה על כל באנר. היא גילתה שאפשר לעשות זאת בארבע חתיכות בלבד. איך היא הצליחה? כמובן, לחתוך את האריה הבריטי יהיה פשע בל יכופר, אז עליכם להיזהר שאף חיתוך לא יעבור דרך אף חלק מהם. לגברות נמסר שאין להתחשב כלל ב"תפרים", ואין לבזבז אף חלק מהחומר. זוהי חידת חיתוך פשוטה למדי אם ניגשים אליה נכון. זכרו שהבאנרים צריכים להיות ריבועים מושלמים, אם כי הם לא צריכים להיות באותו גודל.
-
שאלה 172 - המתנה לחג המולד של גברת סמיילי
הבעת ההנאה של גברת סמיילי הייתה כנה כאשר שש נכדותיה שלחו לה, כמתנה לחג המולד, שמיכת טלאים יפה מאוד, שהן הכינו במו ידיהן. היא נבנתה מחתיכות מרובעות של חומר משי, כולן באותו גודל, ומכיוון שהן הכינו שמיכה גדולה עם ארבעה עשר ריבועים קטנים אלה בכל צד, ברור שנתפרו לתוכה בדיוק `196` חתיכות. עכשיו, שש הנכדות תרמו כל אחת חלק מהעבודה בצורה של ריבוע מושלם (כל ששת החלקים בגודל שונה), אך כדי לחבר אותם ליצירת השמיכה המרובעת היה צורך לפרום את עבודתה של ילדה אחת לשלושה חלקים נפרדים. האם תוכלו להראות כיצד ניתן היה לבצע את החיבורים? כמובן, שאף חלק לא ניתן להפוך.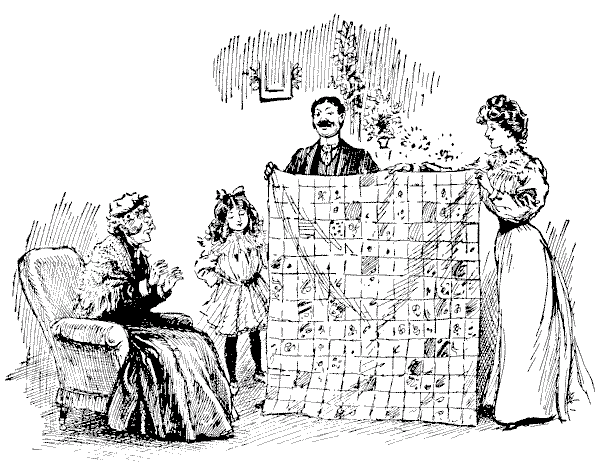
-
שאלה 173 - השמיכה של גברת פרקינס
 ניתן לראות שבמקרה זה שמיכת הטלאים המרובעת בנויה מ-`169` חלקים. החידה היא למצוא את המספר הקטן ביותר האפשרי של חלקים מרובעים שמהם יכולה להיות מורכבת השמיכה ולהראות כיצד ניתן לחבר אותם יחד. או, כדי להציג זאת הפוך, חלקו את השמיכה למספר הקטן ביותר האפשרי של חלקים מרובעים רק על ידי חיתוך התפרים.
נושאים:גאומטריה -> גאומטריה במישור בעיות מינימום ומקסימום קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
ניתן לראות שבמקרה זה שמיכת הטלאים המרובעת בנויה מ-`169` חלקים. החידה היא למצוא את המספר הקטן ביותר האפשרי של חלקים מרובעים שמהם יכולה להיות מורכבת השמיכה ולהראות כיצד ניתן לחבר אותם יחד. או, כדי להציג זאת הפוך, חלקו את השמיכה למספר הקטן ביותר האפשרי של חלקים מרובעים רק על ידי חיתוך התפרים.
נושאים:גאומטריה -> גאומטריה במישור בעיות מינימום ומקסימום קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה -
שאלה 174 - ריבועי הברוקד

קרה שנכחתי בביתה של גברת, כאשר הרמתי משולחן שני ריבועים יפהפיים של ברוקד. הם היו דוגמאות יפהפיות של אומנות מזרחית — שניהם באותו עיצוב, דוגמה משובצת עדינה
."הם לא מעודנים?" אמרה חברתי. "הם הובאו לי על ידי בן דוד שחזר זה עתה מהודו. עכשיו, אני רוצה שתעניק לי קצת עזרה. אתה רואה, החלטתי לחבר אותם יחד כדי ליצור כיסוי כרית מרובע גדול אחד. איך עלי לעשות זאת כדי לשחית את החומר כמה שפחות? כמובן שאני מציעה לבצע את החתכים שלי רק לאורך הקווים שמחלקים את המשבצות הקטנות."

חתכתי את שני הריבועים באופן הרצוי לארבעה חלקים שיכולים להתאים יחד וליצור ריבוע גדול יותר, תוך הקפדה על כך שהדוגמה תתאים כראוי, וכאשר סיימתי שמתי לב שלשניים מהחלקים יש בדיוק אותו שטח; כלומר, כל אחד משני החלקים הכיל את אותו מספר משבצות. האם אתה יכול להראות כיצד בוצעו החתכים בהתאם לתנאים אלה?
-
שאלה 175 - עוד חידת טלאים
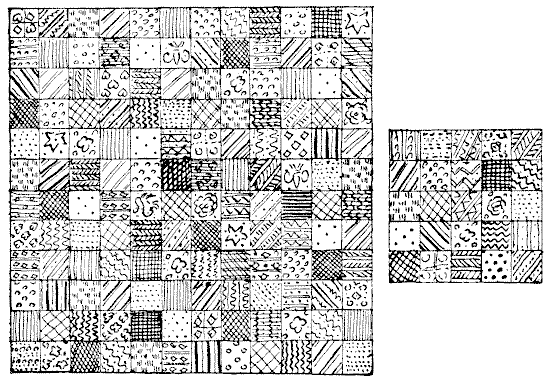 גברת קיבלה משתי חברותיה טלאי משי יפהפה, כפי שניתן לראות באיור. ניתן לראות ששני החלקים מורכבים מריבועים בגודל זהה - אחד `12x12` והשני `5x5`. היא מציעה לחבר אותם יחד וליצור שמיכת טלאים מרובעת אחת, `13x13`, אך כמובן, היא לא תחתוך אף אחד מהחומרים - רק תפרום את התפרים היכן שצריך ותחבר שוב. מה שמבלבל אותה הוא זה. חברה מבטיחה לה שלא צריך יותר מארבעה חלקים בסך הכל כדי לחבר לשמיכה החדשה. האם תוכלו להראות לה כיצד ניתן לפתור את חידת התפירה הקטנה הזו במספר כה מצומצם של חלקים?
נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
גברת קיבלה משתי חברותיה טלאי משי יפהפה, כפי שניתן לראות באיור. ניתן לראות ששני החלקים מורכבים מריבועים בגודל זהה - אחד `12x12` והשני `5x5`. היא מציעה לחבר אותם יחד וליצור שמיכת טלאים מרובעת אחת, `13x13`, אך כמובן, היא לא תחתוך אף אחד מהחומרים - רק תפרום את התפרים היכן שצריך ותחבר שוב. מה שמבלבל אותה הוא זה. חברה מבטיחה לה שלא צריך יותר מארבעה חלקים בסך הכל כדי לחבר לשמיכה החדשה. האם תוכלו להראות לה כיצד ניתן לפתור את חידת התפירה הקטנה הזו במספר כה מצומצם של חלקים?
נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה -
שאלה 176 - חיתוך לינולאום
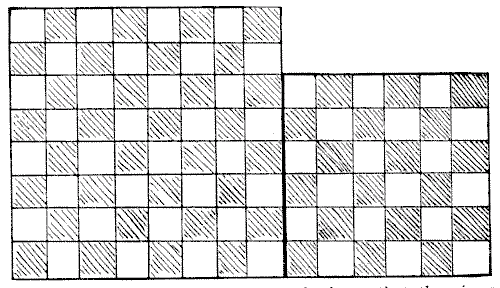 הדיאגרמה כאן מייצגת שני חלקי לינולאום נפרדים. דוגמת המשבצות לא חוזרת על עצמה בגב, כך שלא ניתן להפוך את החלקים. החידה היא לחתוך את שתי הריבועים לארבעה חלקים כך שהם יתאימו זה לזה וייצרו ריבוע מושלם אחד בגודל `10`×`10`, כך שהדוגמה תתאים כראוי, וכך שלחלק הגדול יותר יהיה חלק קטן ככל האפשר שנחתך ממנו.
נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
הדיאגרמה כאן מייצגת שני חלקי לינולאום נפרדים. דוגמת המשבצות לא חוזרת על עצמה בגב, כך שלא ניתן להפוך את החלקים. החידה היא לחתוך את שתי הריבועים לארבעה חלקים כך שהם יתאימו זה לזה וייצרו ריבוע מושלם אחד בגודל `10`×`10`, כך שהדוגמה תתאים כראוי, וכך שלחלק הגדול יותר יהיה חלק קטן ככל האפשר שנחתך ממנו.
נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה -
שאלה 177 - חידת לינולאום נוספת
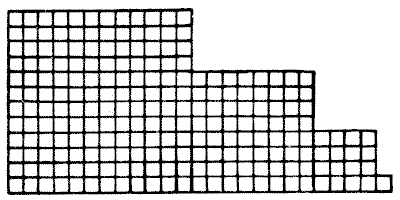
האם תוכלו לחתוך את פיסת הלינולאום הזו לארבע חתיכות שיתאימו זו לזו וייצרו ריבוע מושלם? כמובן שהחיתוכים יכולים להתבצע רק לאורך הקווים.
-
שאלה 178 - קופסת הקרטון
חידה זו אינה קשה, אך יהיה משעשע לגלות את הכלל הפשוט לפתרונה. יש לי קופסת קרטון מלבנית. לשטח החלק העליון `120` אינץ' רבוע, לשטח הצד `96` אינץ' רבוע, ולשטח הקצה `80` אינץ' רבוע. מהם הממדים המדויקים של הקופסה?נושאים:גאומטריה -> גאומטריה במרחב גאומטריה -> חשבון שטחים אלגברה -> משוואות אלגברה -> בעיות מילוליות -
שאלה 179 - גְּנֵבַת חַבְלֵי הַפַּעֲמוֹנִים
שְׁנֵי אֲנָשִׁים פָּרְצוּ לְמִגְדַּל כְּנֵסִיָּה לַיְלָה אֶחָד כְּדֵי לִגְנֹב אֶת חַבְלֵי הַפַּעֲמוֹנִים. שְׁנֵי הַחֲבָלִים עָבְרוּ דֶּרֶךְ חֹרִים בַּתִּקְרָה הָעֲשׂוּיָה עֵץ שֶׁהָיְתָה מֵעֲלֵיהֶם, וְהֵם לֹא בִּזְבְּזוּ זְמַן וְטִפְּסוּ לְרֹאשׁ הַמִּגְדָּל. אָז אִישׁ אֶחָד שָׁלַף אֶת סַכִּינוֹ וְחָתַךְ אֶת הַחֶבֶל מֵעַל רֹאשׁוֹ, וּכְתוֹצָה מִכָּךְ הוּא נָפַל עַל הָרִצְפָּה וְנִפְצַע קָשׁוֹת. חֲבֵרוֹ-הַגַּנָּב קָרָא שֶׁמַּגִּיעַ לוֹ עַל שֶׁהוּא כָּזֶה טִפֵּשׁ. הוּא אָמַר שֶׁהוּא הָיָה צָרִיךְ לַעֲשׂוֹת כְּפִי שֶׁהוּא עוֹשֶׂה, וְעַל כֵּן הוּא חָתַךְ אֶת הַחֶבֶל מִתַּחַת לַמָּקוֹם שֶׁבּוֹ הוּא הֶחְזִיק. אָז, לְתַדְהֵמָתוֹ, הוּא גִּלָּה שֶׁהוּא לֹא בְּמַצָּב טוֹב יוֹתֵר, כִּי אַחֲרֵי שֶׁנִּתְלָה כָּל עוֹד כֹּחוֹ הֶחְזִיק מַעֲמָד, הוּא הֻכְרַח לְהַרְפּוֹת וְלִנְפֹּל לְצַד חֲבֵרוֹ. כָּאן שְׁנֵיהֶם נִמְצְאוּ לְמָחֳרָת בַּבֹּקֶר עִם גְּפָפִים שְׁבוּרִים. מָה הָיָה גֹּבַהּ הַנְּפִילָה שֶׁלָּהֶם? אֶחָד מֵהַחֲבָלִים, כְּשֶׁמָּצְאוּ אוֹתוֹ, רַק נָגַע בָּרִצְפָּה, וְכַאֲשֶׁר מָשַׁכְתָּ אֶת הַקָּצֶה אֶל הַקִּיר, כְּשֶׁהַחֶבֶל מָתוּחַ, הוּא נָגַע בְּנְקֻדָּה שֶׁהִיא רַק שְׁלוֹשָׁה אִינְטְשִׁים מֵעַל הָרִצְפָּה, וְהַקִּיר הָיָה אַרְבָּעָה רֶגֶלִים מֵהַחֶבֶל כְּשֶׁהוּא תָּלוּי בְּמָנוֹחַ. מָה הָאֹרֶךְ שֶׁל הַחֶבֶל מֵהָרִצְפָּה עַד הַתִּקְרָה? -
שאלה 180 - ארבעת הבנים
קוראים יזהו את הדיאגרמה כחבר ותיק מימי נעוריהם. לאיש הייתה אחוזה בצורת ריבוע. הוא הוריש לאלמנתו את הרבע המוצל של האחוזה. את היתר היה צריך לחלק באופן שווה בין ארבעת בניו, כך שכל אחד יקבל קרקע באותו שטח בדיוק ובאותה צורה בדיוק. מוצג לנו איך זה נעשה. אבל המשך הסיפור אינו ידוע כל כך. במרכז האחוזה הייתה באר, המסומנת על ידי הנקודה הכהה, ובנימין, צ'ארלס ודוד התלוננו שהחלוקה אינה "הוגנת", מכיוון שלאAlfred הייתה גישה לבאר הזו, בעוד שהם לא יכלו להגיע אליה מבלי להסיג את גבולו של מישהו אחר. החידה היא להראות כיצד יש לחלק את האחוזה כך שלכל בן תהיה קרקע באותו צורה ובאותו שטח, ולכל אחד תהיה גישה לבאר מבלי לרדת מהשטח שלו.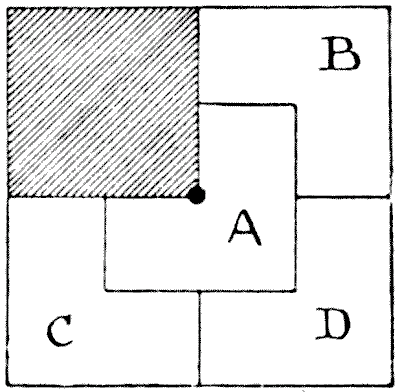 נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה