שעשועונים במתמטיקה, הנרי ארנסט דודני
-
שאלה 191 - חידת הירח
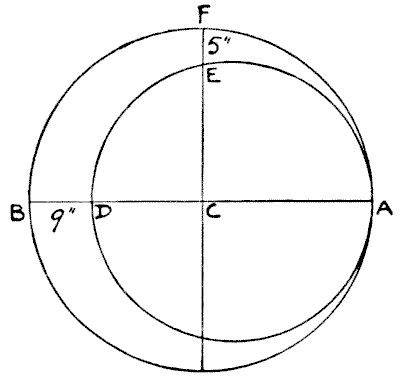 הנה חידה גיאומטרית קלה. הירח נוצר על ידי שני מעגלים, ו-C הוא מרכז המעגל הגדול יותר. רוחב הירח בין B ל-D הוא `9` אינץ', ובין E ל-F הוא `5` אינץ'. מהם הקטרים של שני המעגלים?
הנה חידה גיאומטרית קלה. הירח נוצר על ידי שני מעגלים, ו-C הוא מרכז המעגל הגדול יותר. רוחב הירח בין B ל-D הוא `9` אינץ', ובין E ל-F הוא `5` אינץ'. מהם הקטרים של שני המעגלים?
-
שאלה 192 - קיר החידה
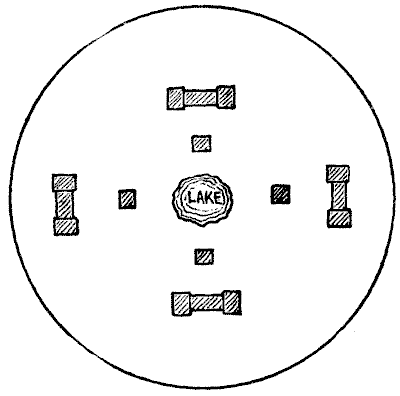 היה אגם קטן, סביבו בנו ארבעה אנשים עניים את בקתותיהם. ארבעה אנשים עשירים בנו לאחר מכן את אחוזותיהם, כפי שמוצג באיור, והם רצו שהאגם יהיה רק לרשותם, ולכן הורו לבנאי להקים את החומה הקצרה ביותר האפשרית שתמנע מהבעלים של הבקתות גישה לאגם, אך תעניק להם גישה חופשית לאגם. איך היה צריך לבנות את החומה?
היה אגם קטן, סביבו בנו ארבעה אנשים עניים את בקתותיהם. ארבעה אנשים עשירים בנו לאחר מכן את אחוזותיהם, כפי שמוצג באיור, והם רצו שהאגם יהיה רק לרשותם, ולכן הורו לבנאי להקים את החומה הקצרה ביותר האפשרית שתמנע מהבעלים של הבקתות גישה לאגם, אך תעניק להם גישה חופשית לאגם. איך היה צריך לבנות את החומה?
-
שאלה 193 - מִכְלָא הַצֹּאן
זהו עובדה מוזרה שהתשובות שניתנות תמיד לכמה מהחידות הידועות ביותר המופיעות בכל ספר קטן של שעשועי בית שפורסם בחמישים או מאה השנים האחרונות הן או בלתי מספקות לחלוטין או שגויות בבירור. עם זאת, נראה שאף אחד לא מבחין בפגמים שלהן. הנה דוגמה: - לחקלאי היה מכלאה העשויה מחמישים גדרות, המסוגלת להכיל רק מאה כבשים. נניח שהוא רצה להגדיל אותו מספיק כדי להכיל כפול ממספר זה, כמה גדרות נוספות הוא צריך? -
שאלה 194 - חומות הגן
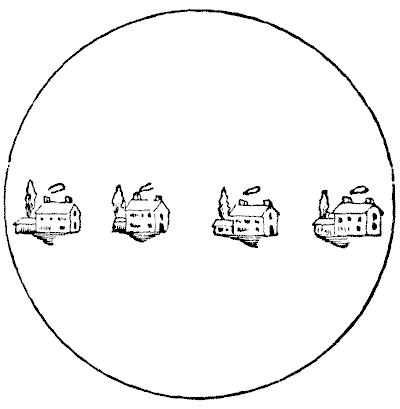
יזם נדל"ן ספקולטיבי מחזיק בשדה עגול, עליו הקים ארבעה קוטג'ים, כפי שמוצג באיור. השדה מוקף בחומה מלבנים, והבעלים התחייב להקים עוד שלושה קירות לבנים, כך שהשכנים לא יוכלו להציץ אחד לשני, אך ארבעת הדיירים מתעקשים שלא תהיה אפליה, ושלכל אחד יהיה בדיוק אותו אורך שטח קיר לעצי הפרי שלו. החידה היא להראות כיצד ניתן לבנות את שלושת הקירות כך שלכל דייר יהיה אותו שטח אדמה, ובדיוק אותו אורך של קיר.
כמובן, כל גן חייב להיות סגור לחלוטין על ידי קירותיו, וחייב להיות אפשרי להוכיח שלכל גן יש בדיוק אותו אורך של קיר. אם החידה נפתרת כראוי, אין צורך במספרים.
נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה -
שאלה 195 - הגן של ליידי בלינדה
ליידי בלינדה היא גננת נלהבת. באיור היא מתוארת כשהיא שקועה בפתרון בעיה קטנה ומהנה שאותה אספר. אחד הגנים שלה הוא בצורת מלבן, מוקף בגדר חיה גבוהה של צמח ההולי, והיא הופכת אותו לגינת ורדים לטיפוח כמה מזני הורדים המשובחים ביותר שלה. היא רוצה להקדיש בדיוק מחצית משטח הגן לפרחים, בערוגה גדולה אחת, ואת המחצית השנייה לשביל המקיף אותו מכל צדדיו ברוחב שווה. גן כזה מוצג בתרשים בתחתית התמונה. כיצד עליה לסמן את הגן בתנאים פשוטים אלה? יש לה רק סרט מדידה, באורך הגן, כדי לעשות זאת, ומכיוון שגדר ההולי עבה וצפופה מאוד, עליה לבצע את כל המדידות בפנים. ליידי בלינדה לא ידעה את המידות המדויקות של הגן, ומכיוון שלא היה צורך שתדע, גם אני לא מציין מידות. זו משימה פשוטה למדי, לא משנה מה גודל או פרופורציות הגן. עם זאת, כמה גננות היו יודעות בדיוק כיצד להמשיך? סרט המדידה יכול להיות פשוט למדי - כלומר, אין צורך שיהיה מדד מדורג. נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים אלגברה -> טכניקה אלגברית אלגברה -> משוואות
נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים אלגברה -> טכניקה אלגברית אלגברה -> משוואות -
שאלה 196 - העז הקשורה
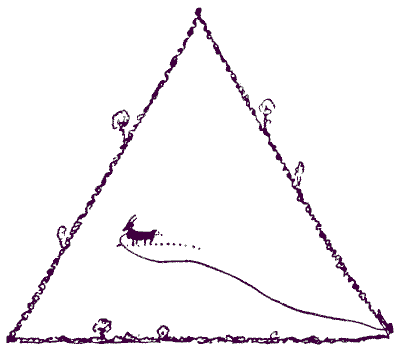 הנה בעיה קטנה שכל אחד צריך לדעת איך לפתור. העז ממוקמת באחו בשטח של חצי אקר, אשר צורתו משולש שווה צלעות. היא קשורה לעמוד בפינה אחת של השדה. מה צריך להיות אורך החבל (באינץ' הקרוב ביותר) כדי שהעז תוכל לאכול רק חצי מהדשא בשדה? ההנחה היא שהעז יכולה לאכול עד סוף החבל.
נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> חשבון זוויות
הנה בעיה קטנה שכל אחד צריך לדעת איך לפתור. העז ממוקמת באחו בשטח של חצי אקר, אשר צורתו משולש שווה צלעות. היא קשורה לעמוד בפינה אחת של השדה. מה צריך להיות אורך החבל (באינץ' הקרוב ביותר) כדי שהעז תוכל לאכול רק חצי מהדשא בשדה? ההנחה היא שהעז יכולה לאכול עד סוף החבל.
נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> חשבון זוויות -
שאלה 197 - חידת המַחְגֵּלִים
זה משונה איך תנאי או מגבלה נוספים יכולים לפעמים להפוך חידה קלה באופן אבסורדי לחידה מעניינת ואולי קשה. אני זוכר שקניתי ברחוב לפני שנים רבות חידה מכנית קטנה שנמכרה בצורה אדירה באותה תקופה. היא כללה מדליה עם חורים, והחידה הייתה להעביר טבעת עם רווח מחור לחור עד שהיא ניתקה סופית. כשהלכתי ברחוב, מהר מאוד רכשתי את הטריק להסיר את הטבעת ביד אחת תוך כדי החזקת החידה בכיס. חבר שהראיתי לו את הפעלול הקטן ניגש להשיג זאת בעצמו, וכשפגשתי אותו כמה ימים לאחר מכן הוא הציג את מומחיותו באומנות. אבל הוא הופתע קצת כשלקחתי ממנו את החידה ואז, תוך כדי החזקת המדליה בין האצבע לאגודל של יד אחת, בסדרה של טלטלות ונענועים קטנים גרמתי לטבעת, בלי שאגע בה אפילו, ליפול על הרצפה. הבוחן הקטן הבא כנראה יתברר כאגוז קשה לפיצוח עבור קוראים רבים, פשוט בגלל התנאים המוגבלים:—
הראו כיצד למצוא בדיוק את אמצעו של כל קו ישר באמצעות מַחְגֵּלִים בלבד. אסור להשתמש בשום סרגל, עיפרון או חפץ אחר—רק במַחְגֵּלִים; ולא יתאפשר שום טריק או התחמקות, כמו קיפול הנייר. אתם חייבים פשוט להשתמש במַחְגֵּלִים בצורה רגילה ולגיטימית.
נושאים:גאומטריה -> גאומטריה במישור -> מעגלים -
שאלה 198 - שמונה מקלות
יש לי שמונה מקלות, ארבעה מהם באורך בדיוק חצי מהאחרים. אני מניח כל אחד מהם על השולחן, כך שהם תוחמים שלושה ריבועים, כולם באותו גודל. איך אני עושה את זה? אסור שיהיו קצוות משוחררים שתלויים מעל. -
שאלה 199 - החידה של פאפוס
זוהי חידה מאת פאפוס, שחי באלכסנדריה בערך בסוף המאה השלישית. זהו המשפט החמישי בספר השמיני של אוספים מתמטיים שלו. אני מציג אותה בצורה שהצגתי אותה לפני כמה שנים תחת הכותרת "החידה של פאפוס", רק כדי לראות כמה קוראים יגלו שהיא מאת פאפוס עצמו. "לאבא של העלמה הקטנה יש שני פיסות קרטון מלבניות בגדלים שונים, והוא גזר פיסה משולשת מאחת מהן, כך שכאשר היא תלויה בחוט מהנקודה A היא תלויה כשהצד הארוך אופקי לחלוטין, כפי שמוצג באיור. הוא הדהים את הילדה בכך שביקש ממנה למצוא את הנקודה A על הכרטיס השני, כדי להפיק תוצאה דומה כאשר הוא נחתך ותלוי בחוט." כמובן, אסור למצוא את הנקודה על ידי גזירות ניסיון. נקודה מוזרה ויפה מעורבת בהצגת החידה הזו. האם הקורא יכול לגלות אותה?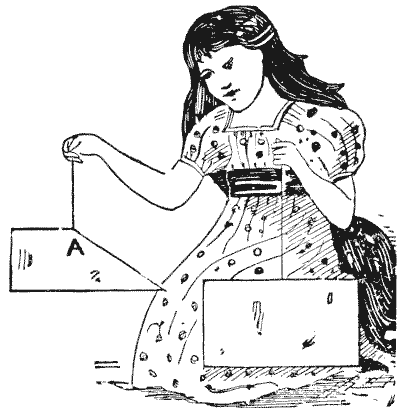 נושאים:גאומטריה -> גאומטריה במישור -> משולשים
נושאים:גאומטריה -> גאומטריה במישור -> משולשים -
שאלה 200 - חידה על עפיפון
בעודי מלווה את ידידי, פרופסור הייפלייט, בתחרות הטסת עפיפונים מדעית בגבעות הדרומיות של סאסקס, נקלעתי לחישוב קטן שאמור לעניין את קוראיי. הפרופסור פרש את החוט שאליו היה מחובר העפיפון שלו מכננת שעליה הוא גולגל בצורה כדורית לחלוטין. כדור חוט זה היה בדיוק שני רגל בקוטר, ולחוט היה קוטר של מאיות אינץ'. מה היה אורך החוט?
עכשיו, שאלה קטנה ופשוטה כזו שכולם יכולים להבין לחלוטין תגרום לרבים להתקשות לענות בכל דרך שהיא. בואו נראה אם, מבלי להיכנס לחישובים מתמטיים מעמיקים כלשהם, נוכל לקבל את התשובה בערך - נניח, בטווח של מייל אחד ממה שנכון! נניח שכאשר החוט מגולגל כולו הכדור מוצק לחלוטין לכל אורכו, ואין צורך להתחשב בציר שעובר דרכו. עם הפשטה זו, אני תוהה כמה קוראים יכולים לציין אפילו בטווח של מייל אחד מהתשובה הנכונה את אורך החוט הזה.
נושאים:גאומטריה -> גאומטריה במרחב אריתמטיקה גאומטריה -> חשבון שטחים אלגברה -> בעיות מילוליות יחידות מידה