שעשועונים במתמטיקה, הנרי ארנסט דודני

  • שאלה 301 - שמונת הכוכבים

    החידה במקרה הזה היא למקם שמונה כוכבים בדיאגרמה כך שאף כוכב לא יהיה באותו קו עם כוכב אחר אופקית, אנכית או אלכסונית. כוכב אחד כבר ממוקם, ואסור להזיז אותו, כך שנשארו רק שבעה לקורא למקם. אבל אסור למקם כוכב על אף אחד מהריבועים המוצללים. יש רק דרך אחת לפתור את החידה הקטנה הזו.

  • שאלה 302 - בעיה בפסיפסים

    אמנות יצירת תמונות או עיצובים באמצעות חיבור חתיכות של חומרים קשים, צבועים באופן טבעי או מלאכותי, היא עתיקה מאוד. היא הייתה ידועה בוודאות בתקופת הפרעונים, ואנו מוצאים התייחסות במגילת אסתר ל"מרצפת בהט ושש ודר וסחרת". נראה כי חלק מהעבודה העתיקה הזו שהגיעה אלינו, במיוחד כמה מהפסיפסים הרומיים, מראים בבירור, גם כאשר העיצוב אינו ניכר בתחילה, כי מחשבה רבה הושקעה בסידורים שנראים לכאורה לא מסודרים. כאשר, למשל, העבודה הופקה עם מספר מוגבל מאוד של צבעים, ישנן עדויות לתחכום רב במניעת גוונים זהים המגיעים בסמיכות זה לזה. קוראות ליידי שמכירות את בניית שמיכות טלאים ידעו כמה רצוי לפעמים, כאשר הן מוגבלות בבחירת החומר, למנוע מחתיכות מאותו חומר להתקרב מדי זו לזו. כעת, החידה הזו תחול במידה שווה על שמיכות טלאים או ריצוף טסלטה.

    ניתן לראות מהדיאגרמה כיצד ניתן לרצף פיסת רצפה מרובעת עם שישים ושתיים אריחים מרובעים משמונת הצבעים סגול, אדום, צהוב, ירוק, כתום, ארגמן, לבן וכחול (המצוינים באותיות הראשונות), כך שאף אריח אינו נמצא בקו אחד עם אריח צבעוני דומה, אנכית, אופקית או אלכסונית. לא ניתן יהיה להציב שישים וארבעה אריחים כאלה בתנאים אלה, אך שני הריבועים המוצלים תפוסים על ידי פתחי אוורור מברזל.

     

    החידה היא זו. יש להסיר את שני פתחי האוורור הללו למיקומים המצוינים על ידי האריחים התחומים כהה, ושני אריחים ממוקמים בריבועי הפינה התחתונה הללו. האם אתה יכול להתאים מחדש את שלושים ושניים האריחים כך ששניים מאותו צבע עדיין לא יהיו בקו?

  • שאלה 303 - מתחת לצעיף

    אם הקורא יבחן את הדיאגרמה לעיל, הוא יראה שמיקמתי שמונה אותיות V, שמונה אותיות E, שמונה אותיות I ושמונה אותיות L בדיאגרמה כך שאף אות אינה נמצאת בקו אחד עם אות דומה לה אופקית, אנכית או אלכסונית. לכן, אף V אינו בקו אחד עם V אחר, אף E עם E אחרת, וכן הלאה. ישנן דרכים רבות ושונות לסדר את האותיות בתנאי זה. החידה היא למצוא סידור שמניב את המספר הגדול ביותר האפשרי של מילים בנות ארבע אותיות, בקריאה מלמעלה למטה ומלמטה למעלה, אחורה וקדימה, או באלכסון. כל החזרות נחשבות למילים שונות, וחמשת הוריאציות שניתן להשתמש בהן הן: VEIL, VILE, LEVI, LIVE ו-EVIL.

    זה יובהר לחלוטין כשאומר שהסידור לעיל מקבל ניקוד של שמונה, מכיוון שהשורה העליונה והתחתונה נותנות שתיהן VEIL; הטורים השני והשביעי נותנים שתיהן VEIL; ושני האלכסונים, החל מה-L בשורה החמישית וה-E בשורה השמינית, נותנים שתיהן LIVE ו-EVIL. לכן ישנן שמונה קריאות שונות של המילים בסך הכל.

    חידת מילים קשה זו ניתנת כדוגמה לשימוש בניתוח לוח שחמט בפתרון דברים כאלה. רק אדם שמכיר את בעיית "שמונה המלכות" יכול לקוות לפתור אותה.

  • שאלה 304 - הריבוע של באשה

    אחת מחידות הקלפים העתיקות ביותר היא של קלוד קספר באשה דה מז'יריאק, שפורסמה לראשונה, אני מאמין, במהדורת `1624` של עבודתו. סדרו מחדש את שישה-עשר קלפי הפנים (כולל האסים) בריבוע כך שבשום שורה של ארבעה קלפים, אופקית, אנכית או אלכסונית, לא יימצאו שני קלפים מאותה צורה או מאותו ערך. זה כשלעצמו די קל, אך נקודה בחידה היא למצוא בכמה דרכים שונות ניתן לעשות זאת. המתמטיקאי הצרפתי הדגול א. לאבוסן, במהדורה המודרנית שלו לבאשה, נותן את התשובה בצורה שגויה. ובכל זאת החידה ממש די קלה. כל סידור מייצר עוד שבעה על ידי סיבוב הריבוע והשתקפותו במראה. באשה מחשיב אותם כשונים זה מזה.

    שימו לב ל"שורה של ארבעה קלפים", כך שהאלכסונים היחידים שעלינו להתייחס אליהם כאן הם שני הארוכים.

  • שאלה 305 - קוביות האותיות - שלושים ושש

    האיור מייצג קופסה המכילה שלושים ושש קוביות אותיות. החידה היא לסדר מחדש את הקוביות כך שאף A לא יהיה בקו אנכי, אופקי או אלכסוני עם A אחר, אף B עם B אחר, אף C עם C אחר, וכן הלאה. תגלו שאי אפשר להכניס את כל האותיות לקופסה בתנאים אלה, אך העניין הוא למקם כמה שיותר. כמובן שאסור להשתמש באותיות אחרות מלבד אלה המוצגות.

  • שאלה 306 - לוח השחמט הצפוף

    החידה היא לסדר מחדש את חמישים ואחד הכלים על לוח השחמט כך שאף מלכה לא תתקוף מלכה אחרת, אף צריח לא יתקוף צריח אחר, אף רץ לא יתקוף רץ אחר, ואף פרש לא יתקוף פרש אחר. אין להתחשב בהתערבותם של כלים מסוג אחר מאלה הנדונים - כלומר, שתי מלכות ייחשבו כתוקפות זו את זו, למרות שייתכן שיהיו, למשל, צריח, רץ ופרש ביניהן. וכך גם לגבי הצריחים והרצים. אין זה קשה להיפטר מכל סוג של כלי בנפרד; הקושי נובע כאשר צריך למצוא מקום לכל הסידורים על הלוח בו זמנית.

  • שאלה 307 - המונים הצבעוניים

    הדיאגרמה מייצגת עשרים וחמישה מונים צבעוניים: אדום, כחול, צהוב, כתום וירוק (המצוינים על ידי האותיות הראשונות שלהם), וישנם חמישה מכל צבע, ממוספרים `1, 2, 3, 4` ו-`5`. הבעיה היא לסדר אותם בריבוע כך שאף צבע או מספר לא יחזרו על עצמם באף אחת מחמש השורות, חמש העמודות ושני האלכסונים. האם תוכלו לסדר אותם מחדש?

  • שאלה 308 - אומנות ליקוק הבולים העדינה

    חוק הביטוח הוא מקור פורה ביותר לפאזלים משעשעים, במיוחד משעשעים אם אתה במקרה נמנה עם הפטורים. ההקדמה של אדם לאומנות ליקוק הבולים העדינה מעלה את החידה הקטנה הבאה: אם יש לך כרטיס המחולק לשישה עשר מקומות (`4` × `4`), ומסופקים לך שפע של בולים בערכים של `1`d., `2`d., `3`d., `4`d., ו-`5`d., מהו הערך הגדול ביותר שתוכל להדביק על הכרטיס אם שר האוצר אוסר עליך להניח בול בקו ישר (כלומר, אופקית, אנכית או אלכסונית) עם בול אחר בעל ערך דומה? כמובן, ניתן להדביק רק בול אחד במקום אחד. הקורא כנראה יגלה, כשהוא יראה את הפתרון, שבדומה לבולים עצמם, הוא הוכה. סביר להניח שיחסרו לו שני פני מהמקסימום. חבר שאל את הדואר כיצד ניתן לעשות זאת; אך הם שלחו אותו לפקיד המכס והבלו, ששלח אותו לנציבי הביטוח, ששלחו אותו לאגודה מאושרת, אשר שלחה אותו בחילול קודש - אך לא משנה.

  • שאלה 309 - ארבעים ותשעה האסימונים

    האם תוכלו לסדר מחדש את ארבעים ותשעה האסימונים שלמעלה בריבוע כך שאף אות, וגם אף מספר, לא יהיו באותו קו עם אחד דומה, אנכית, אופקית או אלכסונית? כאן אני, כמובן, מתכוון לקווים המקבילים לאלכסונים, במובן של לוח השחמט.

  • שאלה 310 - שלוש הכבשים

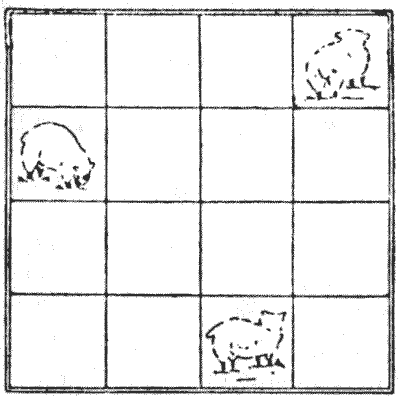    לחקלאי היו שלוש כבשים וסידור של שש עשרה מכלאות, המחולקות על ידי גדרות באופן המצוין באיור. בכמה דרכים שונות הוא יכול למקם את הכבשים האלה, כל אחת במכלאה נפרדת, כך שכל מכלאה תהיה מאוכלסת או בשורה (אופקית, אנכית או אלכסונית) עם כבשה אחת לפחות? נתתי סידור אחד שמקיים את התנאים. כמה אחרים אתה יכול למצוא? אין לספור היפוכים ושיקופים כדברים שונים. הקורא רשאי להתייחס לכבשים כמלכות. הבעיה היא אז למקם את שלוש המלכות כך שכל משבצת תהיה מאוכלסת או מותקפת על ידי מלכה אחת לפחות - במספר המרבי של דרכים שונות.