שעשועונים במתמטיקה, הנרי ארנסט דודני
-
שאלה 331 - המחליקן המדעי

ניתן לראות שהמחליקן סימן על הקרח שישים וארבע נקודות או כוכבים, והוא מציע להתחיל מהמיקום הנוכחי שלו ליד הפינה ולהיכנס לכל אחת מהנקודות בארבעה עשר קווים ישרים. איך הוא יעשה זאת? כמובן שאין התנגדות לכך שהוא יעבור על פני כל נקודה יותר מפעם אחת, אבל המהלך הישר האחרון שלו חייב להחזיר אותו למיקום שממנו הוא התחיל.
זה רק עניין של לקחת את העיפרון ולהתחיל מהמקום שבו רגלו של המחליקן נחה כרגע, ולמחוק את כל הכוכבים בארבעה עשר קווים ישרים רצופים, ולחזור לנקודה ממנה יצאתם.
-
שאלה 332 - ארבעים ותשעה הכוכבים
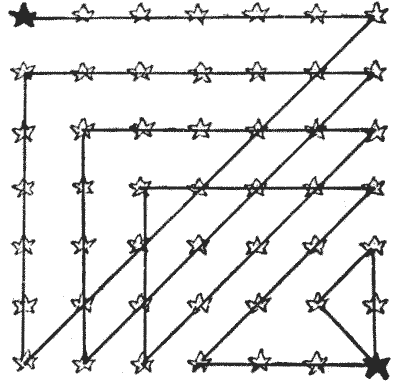 החידה במקרה זה היא פשוט לקחת את העיפרון שלך, ולהתחיל מכוכב שחור אחד, למחוק את כל הכוכבים בשנים עשר קווים ישרים, ולסיים בכוכב השחור השני. ניתן לראות שהניסיון המוצג באיור דורש חמישה עשר קווים. האם אתה יכול לעשות זאת בשנים עשר? כל פנייה חייבת להתבצע על כוכב, והקווים חייבים להיות מקבילים לצדדים ולאלכסונים של הריבוע, כפי שמוצג. במקרה זה אנו עוסקים בלוח שחמט בעל ממדים מופחתים, אך נדרשים רק מהלכי מלכה (מבלי לצאת מגבולות הלוח, כפי שהיה במקרה האחרון).
נושאים:קומבינטוריקה -> תורת הגרפים
החידה במקרה זה היא פשוט לקחת את העיפרון שלך, ולהתחיל מכוכב שחור אחד, למחוק את כל הכוכבים בשנים עשר קווים ישרים, ולסיים בכוכב השחור השני. ניתן לראות שהניסיון המוצג באיור דורש חמישה עשר קווים. האם אתה יכול לעשות זאת בשנים עשר? כל פנייה חייבת להתבצע על כוכב, והקווים חייבים להיות מקבילים לצדדים ולאלכסונים של הריבוע, כפי שמוצג. במקרה זה אנו עוסקים בלוח שחמט בעל ממדים מופחתים, אך נדרשים רק מהלכי מלכה (מבלי לצאת מגבולות הלוח, כפי שהיה במקרה האחרון).
נושאים:קומבינטוריקה -> תורת הגרפים -
שאלה 333 - מסעה של המלכה
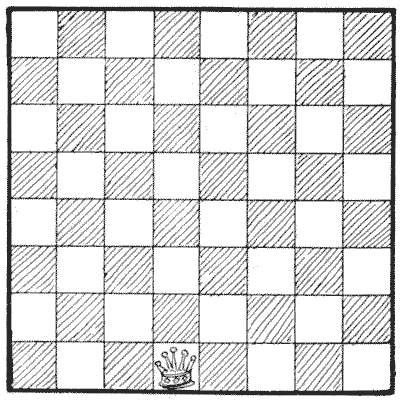 הניחו את המלכה על המשבצת שלה, כפי שמוצג באיור, ואז נסו לגלות את המרחק הגדול ביותר שהיא יכולה לעבור על הלוח בחמישה מהלכי מלכה מבלי לעבור על אף משבצת בפעם השנייה. סמנו את נתיב המלכה על הלוח, ושימו לב היטב גם לכך שאסור לה לחצות את המסלול שלה. זה נראה פשוט מספיק, אבל הקורא עשוי לגלות שהוא נכשל.
הניחו את המלכה על המשבצת שלה, כפי שמוצג באיור, ואז נסו לגלות את המרחק הגדול ביותר שהיא יכולה לעבור על הלוח בחמישה מהלכי מלכה מבלי לעבור על אף משבצת בפעם השנייה. סמנו את נתיב המלכה על הלוח, ושימו לב היטב גם לכך שאסור לה לחצות את המסלול שלה. זה נראה פשוט מספיק, אבל הקורא עשוי לגלות שהוא נכשל.
-
שאלה 334 - סנט ג'ורג' והדרקון
 הנה חידה קטנה על לוח שחמט מצומצם של ארבעים ותשעה משבצות. סנט ג'ורג' רוצה להרוג את הדרקון. הריגת דרקונים הייתה בילוי ידוע שלו, וכאביר, זה היה טבעי שהוא ירצה לבצע את המשימה בסדרת מהלכי פרש. האם תוכלו להראות כיצד, החל מהמשבצת המרכזית, הוא יכול לבקר פעם אחת בלבד בכל משבצת בלוח בשרשרת של מהלכי פרש, ולסיים בלכידת הדרקון במהלך האחרון שלו? כמובן שמגוון דרכים שונות פתוחות בפניו, אז נסו לגלות מסלול שיוצר עיצוב נאה כלשהו כאשר סימנתם כל קפיצה עוקבת על ידי קו ישר ממשבצת למשבצת.
הנה חידה קטנה על לוח שחמט מצומצם של ארבעים ותשעה משבצות. סנט ג'ורג' רוצה להרוג את הדרקון. הריגת דרקונים הייתה בילוי ידוע שלו, וכאביר, זה היה טבעי שהוא ירצה לבצע את המשימה בסדרת מהלכי פרש. האם תוכלו להראות כיצד, החל מהמשבצת המרכזית, הוא יכול לבקר פעם אחת בלבד בכל משבצת בלוח בשרשרת של מהלכי פרש, ולסיים בלכידת הדרקון במהלך האחרון שלו? כמובן שמגוון דרכים שונות פתוחות בפניו, אז נסו לגלות מסלול שיוצר עיצוב נאה כלשהו כאשר סימנתם כל קפיצה עוקבת על ידי קו ישר ממשבצת למשבצת.
-
שאלה 335 - שדות התירס של החוואי לורנס
אחד האזורים היפים ביותר בקרבת לונדון לטיול קיץ הוא אותו חלק של בקינגהאמשייר המכונה עמק הצ'ס—לפחות, כך היה לפני כמה שנים, לפני שנתגלה על ידי הקבלן הספקולטיבי. בתחילת המאה הנוכחית חי, לא רחוק מלטיימרס, חקלאי מכובד אך תמהוני בשם לורנס. אחד הרעיונות המוזרים שלו היה שכל אדם שגר ליד גדות נהר הצ'ס צריך להיות בדרך כלשהי בקיא במשחק האצילי באותו שם, וכדי להטביע עובדה זו על אנשיו ושכניו הוא אימץ לעתים טרמינולוגיה מוזרה. לדוגמה, כאשר אחת הכבשות שלו הציגה לו טלה, הוא היה אומר שהיא "הכתירה רגלי"; כאשר הוא הקים אסם חדש מול הכביש המהיר, הוא כינה זאת "הצרחה בצד המלך"; וכאשר הוא שלח אדם עם אקדח כדי להרחיק את הציפורים של שכנו משדותיו, הוא דיבר על זה כ"תקיפת הצריחים של יריבו". כולם בשכונה נהגו להתבדר מהבדיחות הקטנות של החוואי לורנס, ונער אחד (הליצן של הכפר) שספג משיכות אוזניים מהג'נטלמן הזקן על שגנב את ה"ערמונים" שלו הרחיק לכת עד כדי כך שכינה אותו "מגן שחמט זקן ומטופש!"
באחת השנים היה לו שדה מרובע גדול המחולק לארבעים ותשעה מגרשים מרובעים, כפי שמוצג באיור. הריבועים הלבנים נזרעו בחיטה והריבועים השחורים בשעורה. כשמגיע זמן הקציר הוא נתן הוראה שאנשיו יחתכו תחילה את התירס בחלקה המסומנת `1`, וכי כל חיתוך עוקב יהיה בדיוק מהלך פרש מהאחרון, החיתוך השלושה עשר יהיה בחלקה המסומנת `13`, העשרים וחמישי בחלקה המסומנת `25`, השלושים ושבעה בזו המסומנת `37`, והאחרון, או ארבעים ותשעה, בחלקה המסומנת `49`. זה היה יותר מדי עבור הודג' המסכן, ובכל יום החוואי לורנס היה צריך לרדת לשדה ולהראות על איזה חלק צריך להפעיל. אבל הבעיה אולי לא תציג קושי לקוראים שלי.

-
שאלה 336 - חידת הגרייהאונד
בחידה זו, עשרים המכלאות אינן מתקשרות זו עם זו באמצעות דלתות, אלא מחולקות על ידי קיר נמוך. הדייר הבודד הוא הגרייהאונד שגר במכלאה בפינה השמאלית העליונה. כאשר ניתנת לו החופש, עליו להשיג אותו על ידי ביקור בכל מכלאה פעם אחת בלבד בסדרת מהלכי פרש, תוך סיום בפינה הימנית התחתונה, הפתוחה לעולם. הקווים בדיאגרמה לעיל מראים פתרון אחד. החידה היא לגלות בכמה דרכים שונות יכול הגרייהאונד לצאת כך ממכלאת הפינה שלו.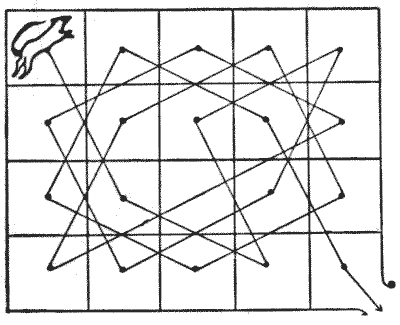 נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים -
שאלה 337 - ארבעת הקנגורו
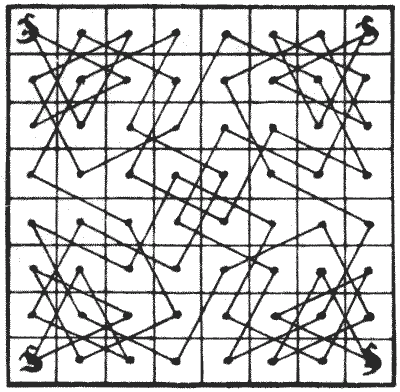 בהציגי בעיה קטנה מחבר העמים, עלי להסביר תחילה שהדיאגרמה מייצגת את שישים וארבעת השדות, כולם מגודרים כראוי זה מזה, של התיישבות אוסטרלית, אם כי אני בקושי צריך לומר שהקרובים שלנו "שם למטה" תמיד כן מסדרים את אדמתם בצורה שיטתית ומדויקת זו. ניתן לראות שבכל אחת מארבע הפינות יש קנגורו. מדוע לקנגורו יש העדפה בולטת לחלקות פינתיות מעולם לא הוסבר בצורה משביעת רצון, וזה לא יהיה במקום לדון בנקודה זו כאן. עלי להוסיף גם כי קנגורו, כפי שידוע, תמיד קופצים במה שאנו מכנים "מהלכי פרש." למעשה, שחקני שחמט כנראה היו מאמצים את המונח הטוב יותר "מהלך קנגורו" אם השחמט לא היה מומצא לפני קנגורו.
בהציגי בעיה קטנה מחבר העמים, עלי להסביר תחילה שהדיאגרמה מייצגת את שישים וארבעת השדות, כולם מגודרים כראוי זה מזה, של התיישבות אוסטרלית, אם כי אני בקושי צריך לומר שהקרובים שלנו "שם למטה" תמיד כן מסדרים את אדמתם בצורה שיטתית ומדויקת זו. ניתן לראות שבכל אחת מארבע הפינות יש קנגורו. מדוע לקנגורו יש העדפה בולטת לחלקות פינתיות מעולם לא הוסבר בצורה משביעת רצון, וזה לא יהיה במקום לדון בנקודה זו כאן. עלי להוסיף גם כי קנגורו, כפי שידוע, תמיד קופצים במה שאנו מכנים "מהלכי פרש." למעשה, שחקני שחמט כנראה היו מאמצים את המונח הטוב יותר "מהלך קנגורו" אם השחמט לא היה מומצא לפני קנגורו.החידה היא פשוטה. בוקר אחד כל קנגורו יצא לקפיצת הבוקר שלו, ובשש עשרה קפיצות פרש רצופות ביקר בחמישה עשר שדות שונים וחזר לפינה שלו. אף שדה לא ביקר על ידי יותר מאחד הקנגורו. הדיאגרמה מראה כיצד הם הסדירו את העניינים. מה שמבקשים מכם לעשות הוא להראות כיצד הם יכלו לבצע את המעשה מבלי שאף קנגורו יחצה את הקו האופקי באמצע הריבוע שמחלק את הלוח לשני חלקים שווים.
נושאים:קומבינטוריקה -> תורת הגרפים קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות -
שאלה 338 - הלוח בתאים

איננו יכולים לחלק את לוח השחמט הרגיל לארבעה תאים ריבועיים שווים, ולתאר מסע שלם, או אפילו מסלול, בכל תא. אבל אנחנו יכולים לחלק אותו לארבעה תאים, כפי שמוצג באיור, שניים המכילים כל אחד עשרים משבצות, ושניים האחרים מכילים כל אחד שתים עשרה משבצות, ובכך להשיג חידה מעניינת. אתם מתבקשים לתאר מסע חוזר ונכנס שלם על הלוח הזה, החל מאיפה שתרצו, אך לבקר בכל משבצת בכל תא עוקב לפני שעוברים לתא אחר, ולבצע את הקפיצה הסופית חזרה למשבצת ממנה יצא הפרש. זה לא קשה, אבל יתגלה כמבדר מאוד ולא חסר תועלת.
האם "מסע" חוזר ונכנס או "נתיב" פרש שלם אפשרי או לא על לוח מלבני ממדים נתונים תלוי לא רק בממדים שלו, אלא גם בצורה שלו. מסע אינו אפשרי באופן ברור על לוח המכיל מספר אי-זוגי של תאים, כגון `5` על `5` או `7` על `7`, מהסיבה הבאה: כל קפיצה עוקבת של הפרש חייבת להיות ממשבצת לבנה לשחורה ושחורה ללבנה לסירוגין. אבל אם יש מספר אי-זוגי של תאים או משבצות חייבת להיות משבצת אחת יותר מצבע אחד מאשר מהצבע השני, לכן הנתיב חייב להתחיל ממשבצת בצבע שנמצא בעודף, ולהסתיים בצבע דומה, ומכיוון שמהלך פרש מצבע אחד לצבע דומה הוא בלתי אפשרי, הנתיב לא יכול להיות חוזר ונכנס. אבל מסע מושלם יכול להתבצע על לוח מלבני בכל מימד, בתנאי שמספר המשבצות יהיה זוגי, ומספר המשבצות בצד אחד לא יהיה קטן מ-`6` ובצד השני לא יהיה קטן מ-`5`. במילים אחרות, הלוח המלבני הקטן ביותר שבו אפשרי מסע חוזר ונכנס הוא לוח בגודל `6` על `5`.
נתיב פרש שלם (לא חוזר ונכנס) על פני כל המשבצות של לוח לעולם אינו אפשרי אם יש רק שתי משבצות בצד אחד; וגם לא אפשרי על לוח ריבועי ממדים קטנים מ-`5` על `5`. כך שעל לוח `4` על `4` אנחנו לא יכולים לתאר מסע פרש וגם לא נתיב פרש שלם; אנחנו חייבים להשאיר משבצת אחת לא מבוקרת. אבל על לוח `4` על `3` (המכיל ארבע משבצות פחות) ניתן לתאר נתיב שלם בשש עשרה דרכים שונות. זה עשוי לעניין את הקורא לגלות את כולן. כל נתיב שמתחיל ומסתיים במשבצות שונות נספר כאן כפתרון שונה, ואפילו מסלולים הפוכים נקראים שונים.
-
שאלה 339 - מסעי ארבעת הפרשים
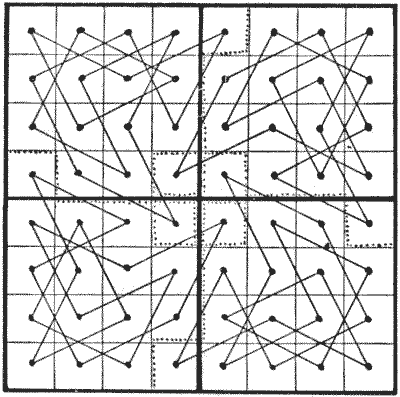 אחזור ואומר שאם לוח שחמט נחתך לארבעה חלקים שווים, כפי שמסומן על ידי הקווים הכהים באיור, לא ניתן לבצע מסע פרש, בין אם הוא סגור ובין אם לא, על אחד החלקים. הניסיון הטוב ביותר למסע סגור מוצג, שבו כל פרש צריך לפלוש פעמיים לחלקים אחרים. החידה היא לחתוך את הלוח באופן שונה לארבעה חלקים, שכל אחד מהם באותו גודל וצורה, כך שניתן יהיה לבצע מסע פרש סגור על כל חלק. חיתוכים לאורך הקווים המקווקווים לא יועילו, מכיוון שארבעת הריבועים המרכזיים של הלוח יהיו מנותקים או תלויים בחוט דקיק.
אחזור ואומר שאם לוח שחמט נחתך לארבעה חלקים שווים, כפי שמסומן על ידי הקווים הכהים באיור, לא ניתן לבצע מסע פרש, בין אם הוא סגור ובין אם לא, על אחד החלקים. הניסיון הטוב ביותר למסע סגור מוצג, שבו כל פרש צריך לפלוש פעמיים לחלקים אחרים. החידה היא לחתוך את הלוח באופן שונה לארבעה חלקים, שכל אחד מהם באותו גודל וצורה, כך שניתן יהיה לבצע מסע פרש סגור על כל חלק. חיתוכים לאורך הקווים המקווקווים לא יועילו, מכיוון שארבעת הריבועים המרכזיים של הלוח יהיו מנותקים או תלויים בחוט דקיק.
-
שאלה 340 - מסע הפרשייה הקוביסטי
לפני מספר שנים יצא לי לקרוא איפשהו שאבנית ונדרמונד, מתמטיקאי חכם שנולד ב-`1736` ונפטר ב-`1793`, הקדיש חלק ניכר מזמנו לחקר שאלת מסעי הפרש. מעבר למה שאפשר להבין מכמה אזכורים מקוטעים, אינני מודע לטבע המדויק או לתוצאות מחקריו, אך דבר אחד משך את תשומת ליבי, והייתה זו ההצהרה שהוא הציע את שאלת מסע הפרש על פני שש הפאות של קובייה, כאשר כל פאה היא לוח שחמט. בין אם השיג פתרון ובין אם לא, אינני יודע, אך מעולם לא ראיתי פתרון שפורסם. אז מיד התחלתי לעבוד כדי לשלוט בבעיה מעניינת זו. אולי הקורא ירצה לנסות זאת.