שעשועונים במתמטיקה, הנרי ארנסט דודני
-
שאלה 291 - הבעיה של הגראנד לאמה
לפני זמן רב היה גראנד לאמה שהייתה לו לוח שחמט עשוי זהב טהור, חרוט בצורה מפוארת, וכמובן, בעל ערך רב. מדי שנה נערך טורניר בלהסה בין הכמרים, ובכל פעם שמישהו ניצח את הגראנד לאמה זה נחשב לכבוד גדול, ושמו נכתב על גב הלוח, ותכשיט יקר הוצב במשבצת המסוימת שבה ניתן השחמט. לאחר שהפונטיף הריבוני הזה הובס בארבעה מקרים הוא מת - אולי מצער.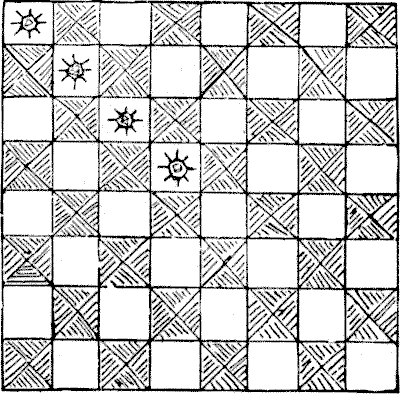 כעת הגראנד לאמה החדש היה שחקן שחמט נחות, והעדיף צורות אחרות של שעשוע תמים, כמו עריפת ראשים של אנשים. אז הוא פסל את השחמט כמשחק משפיל, שלא שיפר לא את המוח ולא את המוסר, וביטל את הטורניר באופן מיידי. ואז הוא שלח לארבעת הכמרים שהייתה להם החוצפה לשחק טוב יותר מגראנד לאמה, ופנה אליהם כדלקמן: "אנשים עלובים וכופרים, המכנים את עצמכם כמרים! האם אינכם יודעים שלטעון ליכולת לעשות משהו טוב יותר מקודמי הוא עבירה שעונשה מוות? קחו את לוח השחמט הזה ולפני שהשחר יעלה על חדר העינויים, חתכו אותו לארבעה חלקים שווים בעלי אותו צורה, שכל אחד מהם מכיל שישה עשר ריבועים מושלמים, עם אחד מהאבנים היקרות בכל חלק! אם תיכשלו בכך, אז יומצאו ספורט אחרים להנאתכם המיוחדת. לכו!" ארבעת הכמרים הצליחו במשימתם שנראתה חסרת סיכוי. האם תוכלו להראות כיצד ניתן לחלק את הלוח לארבעה חלקים שווים, שכל אחד מהם בעל אותו צורה בדיוק, על ידי חיתוכים לאורך הקווים המחלקים את הריבועים, כאשר כל חלק מכיל אחת מהאבנים היקרות?
נושאים:קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה חידות ורבוסים
כעת הגראנד לאמה החדש היה שחקן שחמט נחות, והעדיף צורות אחרות של שעשוע תמים, כמו עריפת ראשים של אנשים. אז הוא פסל את השחמט כמשחק משפיל, שלא שיפר לא את המוח ולא את המוסר, וביטל את הטורניר באופן מיידי. ואז הוא שלח לארבעת הכמרים שהייתה להם החוצפה לשחק טוב יותר מגראנד לאמה, ופנה אליהם כדלקמן: "אנשים עלובים וכופרים, המכנים את עצמכם כמרים! האם אינכם יודעים שלטעון ליכולת לעשות משהו טוב יותר מקודמי הוא עבירה שעונשה מוות? קחו את לוח השחמט הזה ולפני שהשחר יעלה על חדר העינויים, חתכו אותו לארבעה חלקים שווים בעלי אותו צורה, שכל אחד מהם מכיל שישה עשר ריבועים מושלמים, עם אחד מהאבנים היקרות בכל חלק! אם תיכשלו בכך, אז יומצאו ספורט אחרים להנאתכם המיוחדת. לכו!" ארבעת הכמרים הצליחו במשימתם שנראתה חסרת סיכוי. האם תוכלו להראות כיצד ניתן לחלק את הלוח לארבעה חלקים שווים, שכל אחד מהם בעל אותו צורה בדיוק, על ידי חיתוכים לאורך הקווים המחלקים את הריבועים, כאשר כל חלק מכיל אחת מהאבנים היקרות?
נושאים:קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה חידות ורבוסים -
שאלה 292 - החלון של האב המנזר
לפני שנים רבות, האב המנזר מסנט אדמונדסברי, כתוצאה מ"מסירות חזקה מדי לראשו," חלה ולא היה מסוגל לעזוב את מיטתו. כששכב ער, מטלטל את ראשו באי שקט מצד לצד, הנזירים הקשובים הבחינו שמשהו מטריד את מחשבותיו; אך איש לא העז לשאול מה זה יכול להיות, כי האב המנזר היה בעל אופי קשוח, ומעולם לא סבל סקרנות. לפתע קרא לאב ג'ון, והנזיר המכובד ההוא מיהר למיטתו.
"אב ג'ון," אמר האב המנזר, "האם אתה יודע שנולדתי לעולם הנורא הזה בערב חג המולד?
"הנזיר הנהן בהסכמה.
"והאם לא אמרתי לך לעתים קרובות, שנולדתי בערב חג המולד, שאין לי אהבה לדברים שהם אי-זוגיים? תסתכל שם!"
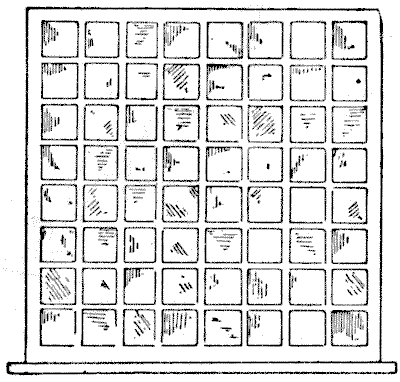
האב המנזר הצביע על חלון המעונות הגדול, שממנו אני נותן סקיצה. הנזיר הביט, והיה נבוך.
"האם אינך רואה ששישים וארבעת האורות מסתכמים למספר זוגי אנכית ואופקית, אך כל הקווים האלכסוניים, למעט ארבעה עשר, הם מספר שהוא אי-זוגי? מדוע זה?"
"אכן, אדוני האב המנזר, זה טבע הדברים, ואי אפשר לשנות זאת."
"לא, אבל זה יש ישתנה. אני מצווה עליך שחלק מהאורות ייחסמו היום, כך שלכל קו יהיה מספר זוגי של אורות. ראה שזה נעשה ללא דיחוי, שמא המרתפים יינעלו לחודש וצרות קשות אחרות יפקדו אותך."
אב ג'ון היה חסר אונים, אך לאחר התייעצות עם מישהו שהיה בקיא בתעלומות מוזרות, נמצאה דרך לספק את גחמתו של האב המנזר. אילו אורות נחסמו, כך שאלה שנותרו הסתכמו למספר זוגי בכל קו אופקית, אנכית ואלכסונית, תוך גרימת ההפרעה המינימלית האפשרית לאור?
-
שאלה 293 - לוח השחמט הסיני
לאיזה מספר גדול של חלקים שונים ניתן לחתוך את לוח השחמט (על ידי חיתוכים לאורך הקווים בלבד), כך שלא יהיו שני חלקים זהים לחלוטין? זכרו שסידור השחור והלבן מהווה הבדל. כך, ריבוע שחור בודד יהיה שונה מריבוע לבן בודד, שורה של שלושה המכילה שני ריבועים לבנים תהיה שונה משורה של שלושה המכילה שני ריבועים שחורים, וכן הלאה. אם לא ניתן להניח שני חלקים על השולחן כך שיהיו זהים לחלוטין, הם נחשבים לשונים. ומכיוון שגב הלוח חלק, לא ניתן להפוך את החלקים.נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים -
שאלה 294 - משפט לוח השחמט

פעם שמתי לעצמי כמשימה משעשעת לנתח לוח שחמט רגיל לאותיות האלף-בית, כך שהן ייצרו משפט שלם. ניתן לראות מהאיור שהחלקים המורכבים יוצרים את המשפט "CUT THY LIFE," עם עצירות בין המילים. המשפט האידיאלי, כמובן, היה בעל עצירה אחת בלבד, אבל לא הצלחתי להשיג זאת.
המשפט הוא קריאה לעבריין להתנתק מחיי הרשע שהוא חי. האם תוכלו לחבר את החלקים האלה כדי ליצור לוח שחמט מושלם?
נושאים:קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה חידות ורבוסים -
שאלה 295 - שמונת הצריחים
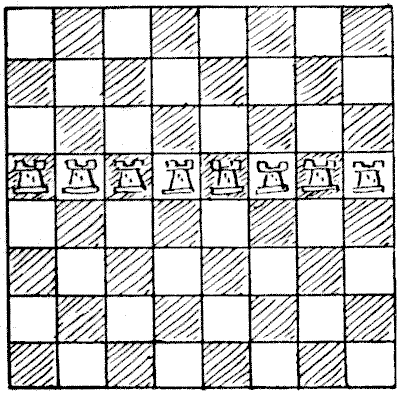 ניתן לראות בדיאגרמה הראשונה שכל משבצת על הלוח מאוכלסת או מותקפת על ידי צריח, וכל צריח "שמור" (אם היו צריחים שחורים ולבנים לסירוגין היינו אומרים "מותקף") על ידי צריח אחר. הצבת שמונת הצריחים על כל שורה או טור תהיה בעלת השפעה זהה. בדיאגרמה `2` כל משבצת שוב מאוכלסת או מותקפת, אך במקרה זה כל צריח אינו שמור. כעת, בכמה דרכים שונות ניתן להציב את שמונת הצריחים על הלוח כך שכל משבצת תהיה מאוכלסת או מותקפת ואף צריח לא יהיה שמור על ידי אחר? אינני רוצה להיכנס לשאלת ההיפוכים והשיקופים בהזדמנות זו, כך שהצבת הצריחים על האלכסון השני תיחשב שונה, וכך גם לגבי חזרות אחרות המתקבלות על ידי סיבוב הלוח.
ניתן לראות בדיאגרמה הראשונה שכל משבצת על הלוח מאוכלסת או מותקפת על ידי צריח, וכל צריח "שמור" (אם היו צריחים שחורים ולבנים לסירוגין היינו אומרים "מותקף") על ידי צריח אחר. הצבת שמונת הצריחים על כל שורה או טור תהיה בעלת השפעה זהה. בדיאגרמה `2` כל משבצת שוב מאוכלסת או מותקפת, אך במקרה זה כל צריח אינו שמור. כעת, בכמה דרכים שונות ניתן להציב את שמונת הצריחים על הלוח כך שכל משבצת תהיה מאוכלסת או מותקפת ואף צריח לא יהיה שמור על ידי אחר? אינני רוצה להיכנס לשאלת ההיפוכים והשיקופים בהזדמנות זו, כך שהצבת הצריחים על האלכסון השני תיחשב שונה, וכך גם לגבי חזרות אחרות המתקבלות על ידי סיבוב הלוח. 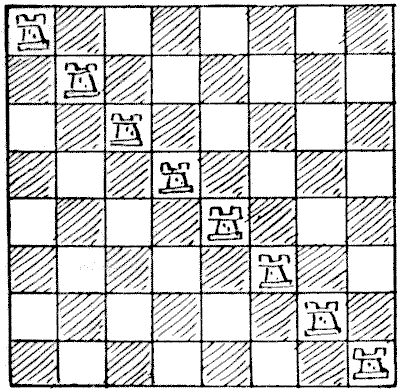 נושאים:קומבינטוריקה -> כלל המכפלה
נושאים:קומבינטוריקה -> כלל המכפלה -
שאלה 296 - ארבעת האריות
החידה היא למצוא בכמה דרכים שונות ניתן להציב את ארבעת האריות כך שלעולם לא יהיה יותר מאריה אחד בכל שורה או עמודה. היפוכים ושיקופים בלבד לא ייחשבו כשונים. לכן, לגבי הדוגמה הנתונה, אם נציב את האריות באלכסון השני, זה ייחשב לאותו סידור. כי אם תחזיקו את הסידור השני מול מראה או תסובבו אותו ברבע סיבוב, תקבלו רק את הסידור הראשון. זוהי חידה קטנה ופשוטה, אך היא דורשת מידה מסוימת של שיקול דעת זהיר. נושאים:קומבינטוריקה
נושאים:קומבינטוריקה -
שאלה 297 - רצים - לא מוגנים
הנח מספר מינימלי ככל האפשר של רצים על לוח שחמט רגיל, כך שכל משבצת בלוח תהיה מאוישת או מותקפת. ניתן לראות שלצריח יש טווח גדול יותר מלרץ: משום שבכל מקום שתציב את הראשון, הוא תמיד יתקוף ארבע עשרה משבצות אחרות; ואילו האחרון יתקוף שבע, תשע, אחת עשרה או שלוש עשרה משבצות, בהתאם למיקום האלכסון עליו הוא מונח. וכדאי כאן לציין שכאשר אנו מדברים על "אלכסונים" בהקשר ללוח השחמט, איננו מגבילים את עצמנו לשני האלכסונים הארוכים מפינה לפינה, אלא כוללים את כל הקווים הקצרים יותר המקבילים לקווים אלה. כדי למנוע אי הבנות בהמשך, כדאי שהקורא ישים לב לעובדה זו בקפידה. -
שאלה 298 - רצים - שמורים
כמה רצים נחוצים כדי שכל משבצת תהיה מאויישת או מותקפת, וכל רץ יהיה שמור על ידי רץ אחר? ואיך ניתן למקם אותם?נושאים:קומבינטוריקה -> גאומטריה קומבינטורית בעיות מינימום ומקסימום קומבינטוריקה -> צביעות -> צביעת שחמט -
שאלה 299 - בישופים בהתכנסות
 המספר הגדול ביותר של רצים שניתן להניח בו זמנית על לוח השחמט, מבלי שרץ אחד יתקוף רץ אחר, הוא ארבעה עשר. אני מראה, בתרשים, את הדרך הפשוטה ביותר לעשות זאת. למעשה, על לוח משובץ ריבועי בעל מספר כלשהו של ריבועים, המספר הגדול ביותר של רצים שניתן להניח ללא תקיפה הוא תמיד שניים פחות מכפול מספר הריבועים בצד. זהו חידה מעניינת לגלות בכמה דרכים שונות ניתן להניח את ארבעה עשר הרצים כך מבלי לתקוף אחד את השני. אתן כלל פשוט ביותר לקביעת מספר הדרכים עבור לוח משובץ ריבועי בעל מספר כלשהו של ריבועים.
נושאים:קומבינטוריקה
המספר הגדול ביותר של רצים שניתן להניח בו זמנית על לוח השחמט, מבלי שרץ אחד יתקוף רץ אחר, הוא ארבעה עשר. אני מראה, בתרשים, את הדרך הפשוטה ביותר לעשות זאת. למעשה, על לוח משובץ ריבועי בעל מספר כלשהו של ריבועים, המספר הגדול ביותר של רצים שניתן להניח ללא תקיפה הוא תמיד שניים פחות מכפול מספר הריבועים בצד. זהו חידה מעניינת לגלות בכמה דרכים שונות ניתן להניח את ארבעה עשר הרצים כך מבלי לתקוף אחד את השני. אתן כלל פשוט ביותר לקביעת מספר הדרכים עבור לוח משובץ ריבועי בעל מספר כלשהו של ריבועים.
נושאים:קומבינטוריקה -
שאלה 300 - שמונה מלכות
המלכה היא ללא ספק הכלי החזק ביותר על לוח השחמט. אם תניח אותה על אחד מארבעת הריבועים במרכז הלוח, היא תוקפת לא פחות מעשרים ושבעה ריבועים אחרים; ואם תנסה להחביא אותה בפינה, היא עדיין תתקוף עשרים ואחד ריבועים. ניתן להניח שמונה מלכות על הלוח כך שאף מלכה לא תתקוף מלכה אחרת, וזוהי חידה ותיקה (שהועלתה לראשונה על ידי נאוק ב-`1850`, ויש לה ספרות משלה) לגלות בכמה דרכים שונות ניתן לעשות זאת. אני מראה דרך אחת בתרשים, ויש בסך הכל שתים עשרה דרכים שונות במהותן. שנים עשר אלה מניבים תשעים ושתיים דרכים אם אנו רואים היפוכים ושיקופים כשונים. התרשים הוא במידה מסוימת סידור סימטרי. אם תהפוך את הדף, הוא ישחזר את עצמו בדיוק; אבל אם תסתכל עליו כשאחד הצדדים האחרים בתחתית, תקבל דרך אחרת שאינה זהה. ואז אם תשקף את שתי הדרכים האלה במראה, תקבל עוד שתי דרכים. כעת, כל אחד-עשר הפתרונות האחרים אינם סימטריים, ולכן ניתן להציג כל אחד מהם בשמונה דרכים על ידי היפוכים ושיקופים אלה. כך יובן מדוע שנים עשר הפתרונות השונים במהותם מניבים רק תשעים ושניים סידורים, כפי שאמרתי, ולא תשעים וששה, כפי שהיה קורה אילו כל שנים עשר לא היו סימטריים. כדאי שתהיה הבנה ברורה בעניין ההיפוכים והשיקופים כאשר עוסקים בחידות על לוח השחמט. האם הקורא יכול להניח את שמונה המלכות על הלוח כך שאף מלכה לא תתקוף מלכה אחרת, וכך שאף שלוש מלכות לא יהיו בקו ישר בכל כיוון אלכסוני? מבט נוסף בתרשים יראה שהסידור הזה לא יענה על התנאים, כי בשני הכיוונים המצוינים בקווים המקווקווים יש שלוש מלכות בקו ישר. יש רק דרך אחת מתוך שתים עשרה הדרכים הבסיסיות שתפתור את החידה. האם אתה יכול למצוא את זה?
האם הקורא יכול להניח את שמונה המלכות על הלוח כך שאף מלכה לא תתקוף מלכה אחרת, וכך שאף שלוש מלכות לא יהיו בקו ישר בכל כיוון אלכסוני? מבט נוסף בתרשים יראה שהסידור הזה לא יענה על התנאים, כי בשני הכיוונים המצוינים בקווים המקווקווים יש שלוש מלכות בקו ישר. יש רק דרך אחת מתוך שתים עשרה הדרכים הבסיסיות שתפתור את החידה. האם אתה יכול למצוא את זה?